Russia, Taganrog, Taganrog State University of Radioengineering

e-mail: lsb@pbox.ttn.ru

Abstract: The questions of the decision making on the bases of the fuzzy expert information are considered. Values of the syntax-independent linguistic variables are the input and output parameters of the decision making process. The method of the definition of the truth degree of the fuzzy propositions is considered. The method of the membership function of the values of the syntax-independent linguistic variable is observed also.

Россия, Таганрог, Таганрогский Государственный Радиотехнический Университет

e-mail: lsb@pbox.ttn.ru

Аннотация: Рассмотрены вопросы принятия решения на основе нечеткой экспертной информации. Входными и выходными параметрами процесса принятия решения являются значения синтаксически-независимых лингвистических переменных. Предложен метод определения степени истинности нечетких высказываний. Рассмотрен метод построения функций принадлежности синтаксически-независимых лингвистических переменных.

In the selection of decision with using of fuzzy expert information, the schemes of decision making (DM) could be divided into two classes. The first class includes the classification schemes, in which possible decisions are limited. For example: to increase, to keep without any modification, or to decrease the speed; to choose one of the meanings 1, 2, 4, 5 and so on. The second class includes the DM schemes, in which the set of possible values of output parameter is countless. For example: the interval of the values set of the real numbers, the value of linguistic variable, which is determined in the interval of the real numbers and so on.

The method of DM is founded and offered in this paper, in the case when the values of input and output parameters of DM process are syntax-independent linguistic variables [Malyshev, Bershtein, Bozhenuk 1991]. Otherwise, such linguistic variables, those values are generated not on the basis of a grammar [Zadeh 1972], but are determined by their names, which are proceed from the nature of linguistic variables. For example, let the linguistic variable with name “pressure” has the basis value “small”, “middle” and “big”. Then, its arbitrary syntax-independent values could be such propositions as: “about 25 atmospheres”, “nearly 12 atmospheres” and so on.

Let DM process be characterized by the parameter V value choice, that is influenced by X, Y, ..., Z values of parameters. Let , , ,..., be the linguistic variables with the sets of the base values accordingly , , ,..., and . We will represent an expert information about decision making as a system of the fuzzy propositions [Malyshev, Bershtein, Bozhenuk 1991]:

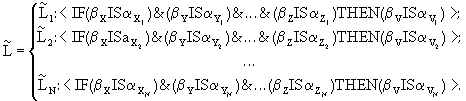
Here , ,..., and .

Let be the generalized linguistic variable [Borisov, Alekseev, Krumberg 1982] on the set of values of the input parameter . The fuzzy propositions are performed in the form of: . Here is the fuzzy proposition and is the fuzzy proposition . Otherwise, fuzzy expert information about DM process is the correspondence, that reflects the base value of generalized linguistic variable from the m-measured space to the one measured space . The DM problem consists of the interpolation of this correspondence on the arbitrary syntax-independent values of linguistic variables and .

Let be the arbitrary (not basic) value of generalized linguistic variable . It is suggested to chose such value of linguistic variable , for which the truth degree of the modus ponens rule for a fuzzy scheme of the inference

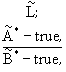(1)

takes its maximum value. Here and - are the propositions and . The truth degree of the modus ponens rule for the inference scheme (1) will be defined by the expression:

. (2)

Here N is a number of propositions in the system . is a truth degree of the fuzzy proposition relatively to the fuzzy proposition . is a truth degree of the fuzzy proposition relatively to the fuzzy proposition .

In the works [Malyshev, Bershtein, Bozhenuk 1991; Bershtein, Bozhenuk, Rozenberg 1998], the algorithms of finding the value of the output parameter in the case, when the propositions and are nonfuzzy, otherwise, when the input and output parameters of DM process have concrete values and , were offered.

For using the fuzzy scheme of the inference (1) in the case than the input and output parameters of DM process are the syntax-independent linguistic variables, it is necessary to solve the following two problems:

First problem - to determine of the semantics of syntax-independent linguistic variables. Otherwise, it is necessary to form and to explain some mapping , with a help of which the arbitrary value of the syntax-independent linguistic variable is putting to the correspondence with the membership function

. (3)

Second problem - to define of the truth degree of the fuzzy proposition : relatively to the fuzzy expression : . Here is a base value of the linguistic variable .

For the solving of the first problem are offered the following two methods.

First method. The mapping for the arbitrary meaning generates the membership function , which completely repeats the membership function nearest to the base value of the linguistic variable .

Second method. The mapping for the arbitrary meaning generates the membership function , which is changed continuously from the function to the function . Here, the membership functions and correspond to the base values and . The value sets between them. In the work [Malyshev, Bershtein, Bozhenuk 1991] this method is considered in details in the case than the membership functions of the base variables are represented in the form of functions.

For the definition of the truth degree of the fuzzy proposition relatively to , there was offered the method given in the works [Bellman, Zadeh 1976; Yager 1978], in which the value of the truth degree is defined as: , where .

Otherwise, the truth degree is defined by the fuzzy set on the interval [0,1]. This method is not very comfortable to use. That’s why there was offered a “geometric” method of approach, in which the truth degree is defined as: . Here, is an area of the figure, which is defined by the membership function ; - is the total area, which is defined by the membership functions and . In such interpretation the truth degree is some value from the interval [0,1].

There are some properties of the truth degree.

Property 1. The value .

Property 2. In the common case .

Property 3. Let a syntax-independent linguistic variable is defined on the set X. The set is the set of base values of the linguistic variable . is a fuzzy expression . is a fuzzy expression . The number of expressions for those the truth degree is not zero, is no more than 4 and no less than 2. Otherwise:

. (4)

The first and second attributes follow from the definition of the truth degree.

Let’s see the proof of the third attribute. Let the lowest estimation is not true. Otherwise, for some value there is no more than one base value , the membership function has the intersection with the . Than, there will be certainly found a some value of , for which the membership functions of the all basic values will be equal to 0:

.

This contradicts to the demands, which are produced to the basic values of the linguistic variable [Borisov, Alekseev, Krumberg 1982]. The highest estimation of the statement (4) is proved by the same way.

It is possible to offer the following algorithm for the definition of the values of the syntax-independent linguistic variable :

To determine the semantic of the input value of the generalized linguistic variable . Otherwise we determine the membership function ;

To calculate the values of truth degree , where is a fuzzy expression of the form and are the fuzzy expert expressions of the form .

Among the possible values of the linguistic variable we choose those, for which the truth degree (2) of a fuzzy rule modus ponens for the scheme (1), takes the biggest value. Here - is the fuzzy proposition and are the fuzzy expert propositions .

The considered method of the DM on the base of the definition of the syntax-independent linguistic variable could be used in the different human-machine systems which are making decisions on the base of fuzzy expert information.

References

Zadeh, Lotfi, 1976, The concept of a linguistic variable and its application to approximate reasoning. Moscow/ Mir, USSR.

Malychev, Nicolay; Bershtein, Leonid; Bozhenuk, Aleksander, 1991, Fuzzy models for expert systems in CAD systems. Moskow/ Energoatomizdat, USSR.

Zadeh, Lotfi, 1972, A fuzzy-set-theoretic interpritation of linguistic hedges. J.Cybernetics, vol.2,N.3, pp.4-34.

Borisov, Arkady; Alekseev, Aleksander; Krumberg, Oar, 1982. The models of making decisions on the basis of linguistic variables. Riga/ Zinatne,USSR.

Bershtein, Leonid; Bozhenuk, Aleksander, Rozenberg Igor, 1998, Decision making on the basis of monotonic expert information. 6-th European Congress on Intelligent Techniques and Soft Computing. EUFIT’98. Aachen/ Germany, vol.2, pp.1136-1140.

Bellman, Richard; Zadeh, Lotfi, 1976, Local and fuzzy logics: Memorandum N ERL-M584, Berkeley/ College of Engineering, University of California, USA.

Yager, Ronald, 1978, Linguistic models and fuzzy truths. Intern. J. Man-Machine Studies, vol.10, N4, pp.483-494.