Russia, Taganrog, Taganrog State University of Radioengineering

e-mail: lsb@pbox.ttn.ru

Abstract: The questions of the decision making on the bases of the fuzzy expert information are considered. Values of the syntax-independent linguistic variables are the input and output parameters of the decision making process. The method of the definition of the truth degree of the fuzzy propositions is considered. The method of the membership function of the values of the syntax-independent linguistic variable is observed also.

Россия, Таганрог, Таганрогский Государственный Радиотехнический Университет

e-mail: lsb@pbox.ttn.ru

Аннотация: Рассмотрены вопросы принятия решения на основе нечеткой экспертной информации. Входными и выходными параметрами процесса принятия решения являются значения синтаксически-независимых лингвистических переменных. Предложен метод определения степени истинности нечетких высказываний. Рассмотрен метод построения функций принадлежности синтаксически-независимых лингвистических переменных.

При использовании нечеткой экспертной информации (ЭИ), в зависимости от вида возможных решений, схемы принятия решений (ПР) можно разделить на два класса. К первому классу относятся классификационные схемы, в которых в качестве возможных решений выступает ограниченное, заранее заданное число значений выходного параметра процесса ПР. (Например: увеличить, оставить без изменения, или уменьшить скорость; выбрать одно из значений 1, 2, 4, 5, и так далее.) Ко второму классу относятся схемы ПР, в которых множество возможных значений выходного параметра бесконечно. (Например: интервал множества действительных чисел; значения лингвистической переменной, задаваемой на интервале действительных чисел, и так далее).

В данной работе рассматривается и обосновывается подход к ПР в случае, когда значениями как входных параметров, так и выходного параметра процесса ПР являются синтаксически-независимые лингвистические переменные [Малышев, Берштейн, Боженюк 1991]. То есть, такие лингвистические переменные, значения которых генерируются не на основе некоторой грамматики, а семантика которых определяется не с помощью теоретико-множественных операций над нечеткими множествами [Заде 1991], а определяется своими названиями, исходя из природы лингвистических переменных. Например, пусть лингвистическая переменная с названием “давление” имеет базовые значения “малое”, “среднее” и “большое”. Тогда, ее произвольными синтаксически-независимыми значениями могут являться высказывания: “около 25 атм.”, “близкое к 12 атм.” и так далее.

Пусть процесс ПР характеризуется выбором некоторого значения параметра V, на которое влияют значения параметров X, Y,...,Z. Пусть экспертная информация о выборе решения представлена в виде системы нечетких высказываний [Малышев, Берштейн, Боженюк 1991]:

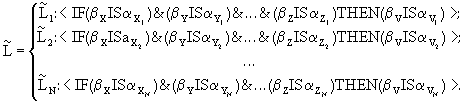
Здесь , , ,..., - лингвистические переменные с множеством базовых значений соответственно , , ,..., и , , ,..., и .

Обозначим через обобщенную лингвистическую переменную определенную на множестве значений входных параметров [Борисов, Алексеев, Крумберг 1982]. Тогда высказывания записаны в виде: . Здесь - высказывание , и - высказывание .

Таким образом, нечеткая ЭИ о процессе ПР задает некоторое соответствие Г, отображающее базовые (экспертные) значения обобщенной лингвистической переменной из n-мерного пространства в одномерное пространство . Задача ПР заключается в “интерполяции” данного соответствия на произвольные синтаксически-независимые значения лингвистической переменной .

Пусть - произвольное (не базовое) значение обобщенной лингвистической переменной . В качестве решения предлагается выбирать такое значение лингвистической переменной , для которого степень истинности правила modus ponens для нечеткой схемы вывода

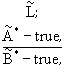(1)

принимает свое наибольшее значение. Здесь и - высказывания вида и соответственно. Величина определяется выражением [1]:

. (2)

Здесь - степень истинности высказывания относительно высказывания , - степень истинности высказывания относительно высказывания .

В работах [Малышев, Берштейн, Боженюк 1991; Берштейн, Боженюк, Розенберг 1998] были предложены алгоритмы нахождения значений выходного параметра в случае, когда высказывания и являются четкими (nonfuzzy), то есть, когда входными и выходными параметрами процесса ПР являются конкретными значениями и .

Для использования нечеткой схемы вывода (1) в случае, когда входными и выходными значениями процесса ПР являются синтаксически-независимые лингвистические переменные, необходимо решить следующие две задачи:

Первая задача - определение семантики синтаксически-независимых лингвистических переменных. То есть, необходимо построить и обосновать некоторое отображение , с помощью которого произвольному значению синтаксически-независимой лингвистической переменной ставится в соответствие функция принадлежности , :

. (3)

Вторая задача - определение степени истинности нечеткого высказывания вида относительно нечетких высказываний вида . Здесь - базовые значения лингвистической переменной .

Для решения первой задачи предлагаются следующие два подхода.

При первом подходе отображение для произвольного значения генерирует функцию принадлежности , которая полностью “повторяет” функцию принадлежности “ближайшего” базового значения лингвистической переменной .

При втором подходе для произвольного значения отображение генерирует функцию принадлежности , которая “непрерывно изменяется” от функции до функции . Здесь функции принадлежности и соответствуют базовым значениям и , между которыми находится значение . В работе [Малышев, Берштейн, Боженюк 1991] данный подход рассмотрен более подробно, в случае, когда функции принадлежности базовых переменных представлены в виде стандартных -функций.

Для определения степени истинности одного нечеткого высказывания относительно другого в работах [Беллман, Заде 1976; Ягер 1978] был предложен подход, в котором значение степени истинности определяется выражением: , где . То есть, степень истинности определяется нечетким множеством на интервале [0,1].

Данная оценка не является удобной для применения. Поэтому, для решения второй задачи был предлагается “геометрический” подход, согласно которому степень истинности определяется отношением: . Здесь - площадь фигуры, определяемая функцией принадлежности , - общая площадь фигур, определяемых функциями принадлежности и . В такой трактовке, степень истинности является некоторым значением из интервала [0,1].

Отметим некоторые свойства предложенной степени истинности:

Свойство 1. Величина .

Свойство 2. В общем случае, .

Свойство 3. Если на множестве Х задана синтаксически-независимая лингвистическая переменная с множеством базовых значений ; - нечеткое высказывание , - нечеткое высказывание вида , тогда число высказываний для которых степень истинности не более 4 и не менее 2. Иначе говоря:

.

Первое и второе свойства вытекают из определения степени истинности. Для доказательства свойства 3 надо показать, что на множестве X функция принадлежности пересекается не менее чем с двумя и не более чет с четырьмя функциями принадлежности базовых значений лингвистической переменной .

Предположим, что нижняя оценка неверна. То есть, существует не более одного базового значения, функция принадлежности которого имеет пересечение с функцией . Тогда, обязательно найдется некоторое значение , для которого функции принадлежности всех базовых значений будут равны 0:

,

что противоречит требованиям, предъявляемым к базовым значениям лингвистической переменной [Борисов, Алеексеев, Крумберг 1982]. Аналогично, доказательство верхней оценки высказывания (3) следует из того, что для любой величины число базовых значений , для которых , не превышает трех.

Из предложенного выше вытекает следующий алгоритм определения значений синтаксически-независимой лингвистической переменной :

1. Определяем семантику входного значения обобщенной лингвистической переменной . Иными словами, определяем функцию принадлежности ;
2. Вычисляем значения степеней истинности , где - нечеткое высказывание вида , а - экспертные высказывания вида .
3. Среди возможных значений лингвистической переменной выбираем такие, для которых степень истинности нечеткого правила modus ponens для схемы вывода (1), определяемая выражением (2) принимали наибольшее значение. Здесь - нечеткое высказывание , а - экспертные высказывания

.

Рассмотренный метод ПР на основе определения синтаксически-независимых лингвистических переменных может быть использован в различных человеко-машинных системах использующих нечеткую экспертную информацию.

Ссылки

Zadeh, Lotfi, 1976, The concept of a linguistic variable and its application to approximate reasoning. Moscow/ Mir, USSR.

Malychev, Nicolay; Bershtein, Leonid; Bozhenuk, Aleksander, 1991, Нечеткие модели для экспертных систем в САПР. Москва/ Энергоатомиздат, USSR.

Zadeh, Lotfi, 1972, A fuzzy-set-theoretic interpritation of linguistic hedges. J.Cybernetics, vol.2,N.3, pp.4-34.

Модели принятия решений на основе лингвистической переменной / А.Н.Борисов, А.В.Алексеев, О.А.Крумберг и др. Рига: Зинатне,1982.-256с.

Bershtein, Leonid; Bozhenuk, Aleksander, Rozenberg Igor, 1998, Decision making on the basis of monotonic expert information. 6-th European Congress on Intelligent Techniques and Soft Computing. EUFIT’98. Aachen/ Germany, vol.2, pp.1136-1140.

Bellman, Richard; Zadeh, Lotfi, 1976, Local and fuzzy logics: Memorandum N ERL-M584, Berkeley/ College of Engineering, University of California, USA.

Yager, Ronald, 1978, Linguistic models and fuzzy truths. Intern. J. Man-Machine Studies, vol.10, N4, pp.483-494.