 |
||
Радченко А.Н.
Россия. Санкт-Петербургский институт информатики и автоматизации РАН e-mail: radchenko@mail. iias. spb. su
МНОГОМЕРНОСТЬ - БЕЗ ПРОКЛЯТИЙ
Обсуждается преодоление колмогоровского барьера сложности путем представления заданной функции многих переменных суперпозицией конечного числа функций с меньшим числом переменных. Показано, что такое представление инвариантно к числу переменных, а его точность зависит от сложности функции, числа композитных функций и пересекаемости областей их определения. Найдено оптимальное значение пересекаемости.
Radchenko A.N.
Russia. Sanct-Petersburg's Institute for Informatics and Automata e-mail:radch@gw2.spiiras.nw.ru
MULTIDIMENSIONALITY - WITHOUT DAMNATIONS
The surmountability of Kolmogorov barrier of complexity by means of representation of the given function of many variables by superposition of finite number of functions of smaller number variables is discussed. It is found, that such representation is invariant to number of variables; representation accuracy depends on the function complexity, number of composite functions and over- lapping of their response regions. The optimum meaning of this overlapping is found.
Проклятие многомерности возникает при
увеличении числа переменных n функции
объекта, которым желают управлять. А. Н.
Колмогоров в докладе "Автоматы и жизнь"
конкретизировал это число, разделив числа на
малые, средние и большие [1]. Огромные
преимущества ЭВМ при работе с малыми и средними
числами вида n и 2n сразу же
исчезают при переходе к большим – вида ![]() . Невозможность их
машинного или ручного перебора наступает уже при
п > 10. В преодолении колмогоровского барьера ЭВМ
столь же бессильна, как и человек, причем этот
вывод нельзя изменить никаким дальнейшим
улучшением параметров ЭВМ. Однако, в отличие от
ЭВМ человек и другие живые организмы каким-то
образом умеют управляться с многими тысячами
переменных, легко распознавая образы и решая
сложные комбинаторные и игровые задачи.
. Невозможность их
машинного или ручного перебора наступает уже при
п > 10. В преодолении колмогоровского барьера ЭВМ
столь же бессильна, как и человек, причем этот
вывод нельзя изменить никаким дальнейшим
улучшением параметров ЭВМ. Однако, в отличие от
ЭВМ человек и другие живые организмы каким-то
образом умеют управляться с многими тысячами
переменных, легко распознавая образы и решая
сложные комбинаторные и игровые задачи.
Что же отличает обработку информации в живых системах от машинной обработки и, если такие отличия есть, являются ли они принципиальными?
Подход к решению вопроса мы находим в более ранней работе Колмогорова [2]. Не связывая ее с ответом на поставленный вопрос, он доказал теорему существования о представимости функции многих переменных суперпозицией конечного числа функций одной переменной (при выполнении ряда ограничений). Связь этой теоремы с поставленным вопросом и биологическим прототипом увидел Р. Хехт-Ниелсен [З]. Он обнаружил аналогию теоремы со структурой нейронных сетей, чем возбудил большой и все возрастающий интерес к последним. Не являются ли нейронные сети конструктивным и практически достижимым аналогом теоремы? В этом случае обработка информации в технических устройствах могла бы быть столь же эффективной, как и живых организмах! Эта аналогия вызвала бурю работ по нейронным сетям. Неуспехи не подорвали энтузиазма - их объясняли тем, что число m требуемых для аппроксимации функций велико, больше, чем "синапсов", имевшихся тогда в модельной системе СМАС1.
К сожалению, задачи опознания образов, построения движений и др. по-прежнему остаются проблематичными для современных информационных технологий. Поэтому весьма актуален третий шаг в решении колмогоровской задачи. Его сделали Н. Е. Коттер и Т. Дж. Гуиллерм [4]. Базируясь на работах Шпрехера и Лоренца, они отметили возможность ослабления ограничений на композитные функции, указали на возможность их подбора методом обучения в системе СМАС и акцентировали внимание на том, что области определения этих функций, покрывающих область определения исходной функции, пересекаются между собой. Они же предположили, что эти пересечения нужны нейронам для компенсации ошибок аппроксимации (spurious activity), которые, очевидно, зависят и от сложности исходной функции.
Но не возникает ли здесь традиционное "проклятие многомерности"?
Не возникает! Переходя к машинным методам и, следовательно, к булевым функциям (в данном случае со многими тысячами переменных), мы связали их сложность, как с числом переменных n, так и с числом значений (а - число нулей и b - единиц). Имеет смысл рассматривать только функции реальной сложности, когда а + b << 2n. Анализируя аппроксимацию такой функции с помощью т функций меньшей размерности, нам удалось подтвердить, что пересекаемость областей определения композитных функций действительно связана с точностью. Однако эта зависимость оказалась немонотонной - был обнаружен резко выраженный минимум погрешностей и найдена оптимальная пересекаемость подпространств, на которых заданы аппроксимирующие функции. Известный призыв соединять нейроны "каждый с каждым" оказался ложным,
резко ухудшающим аппроксимацию! К счастью, этот призыв обычно технически нереализуем, что и определило некоторые успехи "нейрокомпьтинга".Но главный результат исследования оказался "побочным". Получилось, что заданную функцию можно воспроизвести точно независимо от числа переменных. При этом достаточно, чтобы число композитных функций (импликант) было бы не более чем в е/2 раз больше числа значений исходной функции [5]. Далее обнаружено, что аналогичным (т.е. вполне техническим) образом сетчатка глаза решает задачу острого зрения с помощью больших, многократно пересекающихся (!) рецептивных полей [6]. Эта же теория позволила понять механизмы нейронной памяти и оценить ее параметры [7-8], а также применить критерий минимизации к процессам биологической эволюции. Был найден ответ, на вопрос 40-летней давности - в эпоху ранней кибернетики. Проклятие многомерности преодолимо, причем не только в живой природе.
Для развития новых информационных технологий инвариантность к числу переменных крайне важна, достигается она следующим образом.
Назначим исходную функцию U(x1, x2 ,..., хn) предельно сложной, предположив, что она задана значениями 0 и 1, которые заданы случайным образом (а нулей и b единиц). Потребуем, чтобы а + b << 2n, т.е. будем рассматривать слабо определенные функции. Если число переменных мало и аппроксимируемая функция определена полно, то n следует увеличить, расширив область определения U. Для этого остаточно ввести в качестве аргумента избыточные переменные, например, их комбинации или просто несколько раз повторить имеющиеся переменные.
Область определения исходной функции из 2n точек заполним случайным образом т областями определения аппроксимирующих функций. Каждую из них зададим на V точках. Пусть значения функций во всех областях определения одинаковы, например, единицы. Исходный хаос таких функций мы упорядочим, применив обучение, которое реализуется следующим образом. Удалим ту часть композитных функций, которые покрывают нули исходной функции. Освободившиеся точки n-пространства точно воспроизведут все нули U. Вероятно, что и некоторая часть единиц этой функции окажется правильной, но для этого они не должны попасть в освобожденные или изначально не покрытые подобластями области функции U. Возможно и другое - этого не случится, т.е. произойдут ошибки.
Вероятность р таких ошибок, т. е. вида 1 —> 0, при формировании U вычислена по схеме Бернулли
![]() (1)
(1)
где
q=V/2n - вероятность попадания случайной точки в данную подобласть, (1-q)a - вероятность непопадания ни одной из а нулевых точек функции U в фиксированную подобласть, q(1 - q)a - вероятность того, что в данную область не попадет ни одна из а нулевых точек, но попадет одна из b единичных точек (в этом случае ошибка не возникает). Выражение в квадратных скобках - вероятность ошибки для каждого единичного значения функции U, но ошибка возникнет лишь в случае, если ошибочная ситуация повторится в каждой из т хаотически (независимо) расположенных подобластей.Функция (1) имеет минимум при q = qopt =1/(a+1),что соответствует размеру подобласти Vopt= 2n/(a+1). Обратим внимание, что эта подобласть огромна. Подставляя в (1) оптимальное значение q и замечая, что
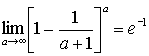 ,
,
получим
![]() (2)
(2)
![]()
Далее воспользуемся критерием пересекаемости подпространств S, где среднее значение
![]()
оптимально при V = Vopt Следовательно,
![]() (3)
(3)
Это выражение дает оптимальное
соотношение L между сложностью функции а
и числом аппроксимирующих ее композитных
функций т, L = а/т ![]() .
.
Используя (3) при замене переменных в (1) относительными значениями
![]() ,
,
получим его в виде, который инвариантен к n:
![]() (4)
(4)
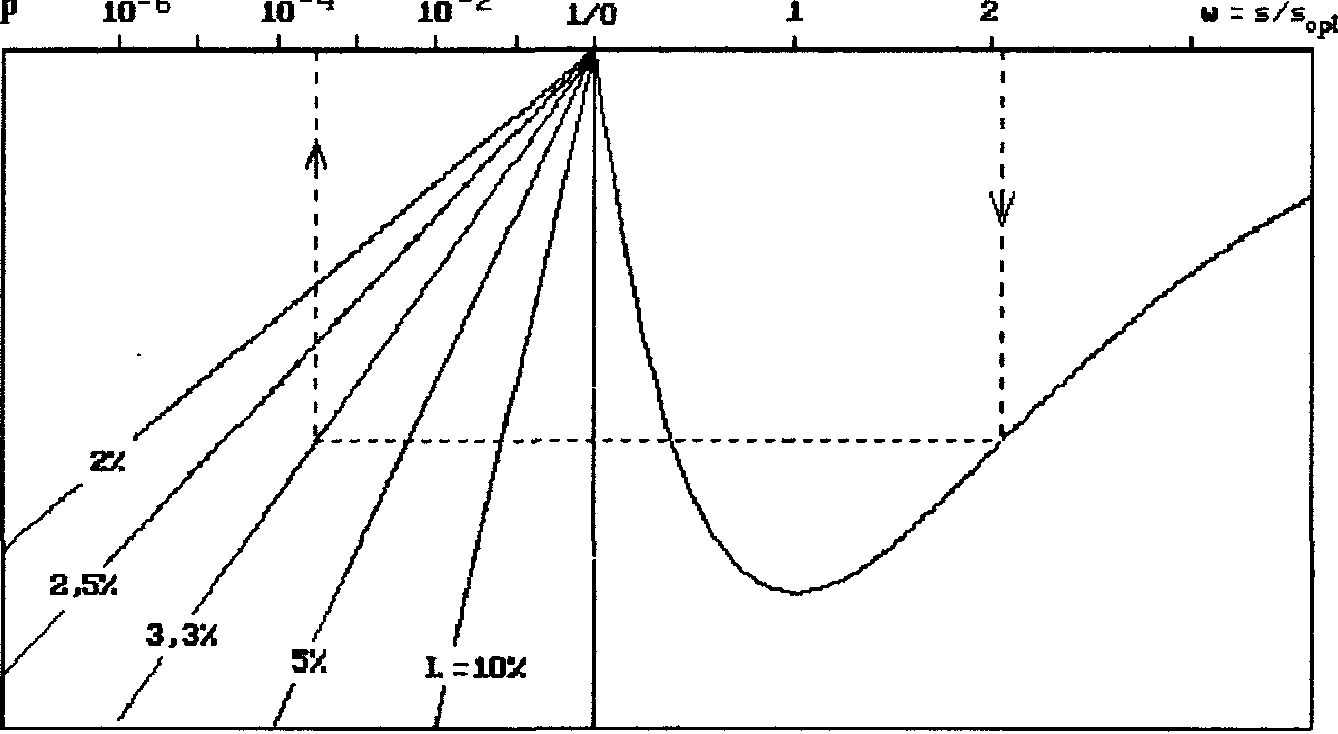
Использованный обучающий алгоритм формирования заданной функции из хаоса подпространств дает высокую точность аппроксимации при S порядка десяти (см. график на рис.1). При таком перекрытии областей определения вернее говорить не об их распределении, а об упаковке n-пространства областями задания композитных функций. Дальнейшее повышение точности возможно, если хаотическое распределение областей определения аппроксимирующих функций заменить 1) более регулярным или 2) согласовать с видом аппроксимируемой функции, что на первый взгляд кажется даже лучше.
Переход от случайного распределения к регулярному мы встречаем в строении рецептивных полей сетчатки глаза, перекрытии углов зрения образующих фасеточный глаз омматидиев, перекрытии рецептивных полей кожной чувствительности и др. Заметное увеличение точности относительно (2, 4) мы получили в эксперименте, выбрав подпространства ортогональными. Идеальную регулярность упаковки n-пространства демонстрируют плотно упакованные коды. Но здесь нет перекрытия, S = 1, и, следовательно, для получения высокой точности метод корректирующих кодов нуждается в модификации.
Согласование с видом функции повсеместно распространено при опознавании образов. Имеются, например, данные о согласовании глаза и мозга лягушки с изображениями насекомых, которыми она питается. Специалисты по опознаванию образов знают, что с помощью современных и будущих суперЭВМ такое согласование невозможно без замены переменных их статистическими параметрами. Иначе, сталкиваясь с проклятием многомерности, придется безуспешно штурмовать колмогоровский барьер сложности. Лягушке, например, не удалось достичь совершенства в опознавании насекомых, хотя на решение задачи был затрачен миллиард лет. На этом фоне использование случайных или частично упорядоченных функций с оптимальной суперпозицией областей определения выглядит экономичнее. К тому же методом итераций [6] задачу можно решить точно, р = 0.
Как и в рассмотренном случае, такое решение достигается без согласования с видом задаваемой функции, т.е. при хаотически размещенных областях определения композитных функций. Это не означает, что согласование вредно. Просто его следует применять после преодоления "проклятия многомерности".
Список литературы
1. Колмогоров А.Н Автоматы и жизнь. В сб. Кибернетика - неограниченные возможности и возможные ограничения. Итоги развития. Наука, М, 1979, с. 10-29.
2. Колмогоров А.Н. О представлении непрерывных функций нескольких переменных в виде суперпозиции непрерывных функций одного переменного и сложения. Доклады АН СССР, 1957, т. 114, вып.5. с. 953-956
3. Hecht-Nielsen R. Kolmogorov's mapping neural networks existence theorem, hi Proc. IEEE First Internal Conference on Neural Networks. 1987. Vol.n, pp. 11-14. San Diego, CA:
80S Printing.
4. Cotter N.E., Guillerm Т. J. The CMAC and a Theorem of Kolmogorov. Neural Networks, 1992, v.3, pp.221-228
5. Радченко А.Н. Аппроксимация и точное формирование булевых функций многих переменных. I. Объем памяти и точность аппроксимации. Изв. АН СССР. Техническая кибернетика. 1985, №1, 148-156.
6. Радченко А.Н. Аппроксимация и точное формирование булевых функций многих переменных. П. Эффективное построение ассоциативной памяти. Там же, 1985, N 2, 98-106.
7. Радченко А.Н. Влияние размеров рецептивных полей сетчатки на точность восприятия изображений. Биофизика, 1991, т. 36. № 36, с. 521-529.
8. Радченко А.Н. Ассоциативная память. Нейронные сети. Оптимизация нейропроцессоров. Санкт-Петербург. Наука. 1998. С.261
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|