 |
||
|
||
Vassili Karassev, Eugin Solojentsev
Russia, St.Petersburg, Institute of Mechanical Engineering
of Russian Academy of Sciences, E_mail: kvv@sapr.ipme.ru
INTELLIGENT SYSTEMS AND LOGICAL AND PROBABILISTIC
RISK MODELS IN BANKS, BUSINESS AND QUALITY
Abstract. The way a complex task of risk assessment is stated. Technique of logical and probabilistic (LP) assessment and analysis of risk with consideration ofgroupes ofuncompatible events (GUE) is described. Accuracy and stability proofs of classification of objects by different methods are showed.
Карасев Василий, Соложенцев Евгений
Россия, Санкт-Петербург, Институт Проблем Машиноведения
Российской Академии Наук, E_mail: kvv@sapr.ipme.ru
ИНТЕЛЛЕКТУАЛЬНЫЕ СИСТЕМЫ И ЛОГИКО-ВЕРОЯТНОСТНЫЕ МОДЕЛИ РИСКА В БАНКАХ, БИЗНЕСЕ И КАЧЕСТВЕ
Аннотация. Изложена постановка комплексной задачи оценки риска. Описана методика логико-вероятностной (ЛВ) оценки и анализа риска с учетом групп несовместных событий (ГНС). Приведены показатели точности и стабильности классификации объектов разными методами.
The present work is devoted to problem of extraction of knowledge from a table "object-signs" in risk tasks. The problem is solved by using of logical and probabilistic approach that was not applied earlier for such purposes. This approach is proposed as alternative to image recognition methods, neural networks and DATA MINING.
There are several ways of solving of tasks of risk assessment. Some methods are based on expert assessments and rating systems (Price Waterhouse). In other methods risk assessment is considered as classification task and discriminatory analysis (L. Breiman, L.Fahrmeier, H.-J. Hofmann) and neural networks (E. Stickel) are used. The risk assessment is made by aggregate of data about object. These data includes a set of signs, even sign has a set of gradations. Discriminant function classifies the object to one of the two subclasses: "good" or "bad". These methods not allows to obtain precise numerical rsik assessment, to establish admissible risk and to assign a price for the risk.
For risk assessment in complex technical systems LP-method is applied (I. Ryabinin, E. Henley, H.Kumamoto). But there are some tasks that were not solved in LP-theory for tasks of business and banks: 1) events are considered on two levels only, while in banks the events has up to 10 levels and the GUE must be used; 2) in banks risk models are associative;
3) task of identification ofLP risk models under statistical data was not being solved earlier.
Statistical data are presented as table "object-signs".
Objects 
are described by set of signs 
, every sign has own set of gradations 
. In description of separate object every sign
j accepts one value 
. So, object is
described by n gradations 
, where 
and 
. Final sign has gradations also, for instance, credit has two gradations: 1 -
was returned; 0 - default.
Risk is described by two values. First - possible damage in result of failure, second - the failure probability. The accuracy of risk model is determined by relative error in classification of objects. Failure risk for object is a probability of object's failure that can be compared with admissible and average risks for set of objects.
We suggest to consider risk task as complex task consist of five separate tasks: 1) numerical risk assessment as probability; 2) classification of object by risk value on "good" or "bad"; 3) determination of price for risk; 4) analysis of contributions of initiating events in object's risk; 5) analysis of contributions of initiating events in average risk of objects in table.
Casual events leading to failure correspond to signs and gradations. Signs are correlate a little and casual events connected with signs are independent. Casual events, corresponding to gradations, forms GUE. We designate events by logical variables and construct logical functions (L-functions).
Binary variable 
for
sign , is equal 
with probability 
,
if sign j led to failure and 
in opposite
case with probability 
. Variable 
for gradation of sign is equal 
, if sign
j has gradation . Y is binary variable for
final sign of failure ofi-object, 
.
L-function for final variable Y that accepts value Y=1 for bad object
and Y=0 for good, we are writing as function of variables 
:
(1)
The object's risk 
is
determined from probabilistic (P) function after orthogonalization (1):
(2)
Frequencies of gradations in objects of table “object-signs” are equal to:
(3)
For every gradation two different probabilities are used. Probabilities
of gradations 
, being in GUE, are equal
to:
(4)
Probabilities of gradations 
, placed in P-function, are equal to:
(5)
For learning and analysis of P-model of risk, average values of
probabilities 
and 
for gradations are used:
(6)
(7)
We'll use also some other average probabilities for table
“object-signs”: a priori 
and
calculated 
risks of objects and
frequencies 
in GUE:
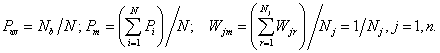(8)
Calculated or assigned admissible risk devotes objects: if then object
is bad, if 
then object is good. Object's
risk 
is calculated always by formula (2)
by placement of appropriate probabilities 
in formula instead of probabilities 
.
Probabilities 
are evaluated by
identification (learning) of P-model of risk by statistical data.
P-model of risk can be learned without consideration or with
consideration of GUE. In these cases the connection between probabilities and 
is determined differently. There is trivial connection between and if GUE are not considered in learning:
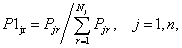(9)
In optimisation task of algorithmical iterative learning of P risk
model by data of table “object-signs” probabilities are evaluated directly but probabilities are calculated by formula (9) for information. In such scheme of learning a
number of evaluated probabilities is equal to: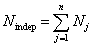 
.
If in learning GUE are not considered then, primarily, probabilities are determined and further it's necessary to move to probabilities . In such scheme a number of probabilities is equal to: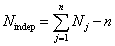 
.
In this case decisions
will more stable due to a number of independent evaluated probabilities is less essentially. In this case, connection
between probabilities for gradations and can be wrote from equations (3), (4), (5) on
basis of well-known Bayes' rule for conditional probabilities:
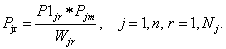(10)
In table a number of objects is not so large therefore there are
gradations with very small frequencies 
, or
equal to 0. Formula (10) cannot be used for connection of probabilities 
and , because 
is in denominator of
expression (10). Therefore, we'll write connection of probabilities for gradations 
and by average values of their probabilities 
and 
for table, calculated by
formulae (6), (7):
(11)
where 
is a ratio of
connection of probabilities and in GUE, 
If P-model of risk was built and probabilities 
, are known then it's possible to determine individual and group
contributions of events, connected with signs and gradations, in object's risk and in
average risk of set of objects. Under this contributions it's possible to make decisions
about risk management for object or set of objects in all (credit activity of bank).
Contributions of signs and gradations in risk are determined with the aid of program on
computer, calculating difference between calculation result (risk) on nominal (optimal)
mode and result (risk), obtained by giving zero to corresponding probabilities of
gradations.
Identification of P-model of risk consist in determination of optimal
probabilities , 
that correspond to gradations of signs.
Objective function in identification task is next: 
, where 
, 
- numbers of bad and good
objects, classified as bad and good correctly.
Task has next limitations: 1) probabilities 
, are positive and belongs to interval [0,1]; 2) average risks of
objects by P-model and statistical data are equal; 3) admissible risk 
is determined on given ratio of wrongly
classified good and bad objects:, where 
-
numbers of bad and good objects by statistical data.
Identification task due to complexity can be solved by algorithmical
methods only. The algorithm of P-model identification is offered where required 
and are generated iteratively in order to maximize F. Iteration number is changed
by condition: 
, where 
- current and earlier achieved value of
objective function.
For calculation of changes of 
two identification methods were developed: method of casual search and method
of small increments. During P-model identification, mistakes in classification of good
objects 
, bad 
and in general 
are
calculated: 
;
.
Scheme of learning of P-model by method of casual search without consideration of GUE was developed also. Identification methods of P-model with and without consideration of GUE gives the same value of objective function but having essentially different proofs of stability of decisions.
LP-technique of risk assessment was approved using “standard” statistical data about 1000 credits. These data was being used earlier for test often different techniques of credit classification. Learning of P-model was made by statistics, risks (default's probability) were determined for 1000 credits and accuracy proofs were calculated. The comparison of techniques in accuracy proofs has shown LP-technique has almost twice more accuracy than classification methods on basis of discriminatory analysis and neural networks (table 1).
Table 1. Accuracy proofs for classification of objects by different methods
N |
Used method |
Еb,% |
Еg,% |
Em,% |
1 |
LDA Resubstitution |
26.0 |
27.9 |
27.3 |
2 |
LDA Leaving-one-out |
28.7 |
29.1 |
29.0 |
3 |
QDA Resubstitution |
18.3 |
28.3 |
25.3 |
4 |
QDA Leaving-one-out |
28.3 |
34.0 |
32.3 |
5 |
CART |
27.7 |
28.9 |
28.5 |
6 |
Neural Network NN1 |
38.0 |
24.0 |
28.2 |
7 |
Neural Network NN2 |
24.0 |
31.2 |
29.0 |
8 |
LP-technique ( without consideration of GUE ) |
16.7 |
20.1 |
19.1 |
9 |
LP-technique ( with consideration of GUE ) |
17.6 |
20.4 |
19.6 |
For the rirst time we have use a proof of classification stability for assessment of quality of different techniques. Depending of method and learning parameters various methods classifies objects differently. The same object in one technique or in one decision can be classified as bad but in another technique or another decision - as good. The number of such objects is about 20% in their general number with same accuracy of models. On basis of results of comparable calculation it was showed that classification methods on basis of neural networks, using essentially more large number of weights and not considering GUE, has more than seven times less classification stability than LP-technique.
Literature
1. Solojentsev E.D., Karassev V.V., Solojentsev V.E. Logical and probabilistic risk models in banks, business and quality. St-Petersburg, Nauka, 1999, -120 pages. (In Russian)
2. Solojentsev E.D., Karasev V.V. The logic and probabilistic method of assessment of credit risks and identification of risk models / International ICSC Congress “Computational intelligence: method and applications (CIMA'99)” / Proceedings: Rochester Institute of Technology, RIT,Rochester,N.Y.,USA, 1999.
3. Karassev V.V. Logical and probabilistic model of credit risk / International Conference Instrumentation in Ecology and Human Safety (IEHS'98) / Proceedings: St-Petersburg State University of Aerospace Instrumentation, 1998, p. 179. (In Russian)
4. Solojentsev E.D, Karassev V.V. About technique of qualitative assessment of credit risk for individuals. - Money and credit, 2/1998 - p. 76-79(In Russian)
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|