 |
||
Krasnoshtanov A. P., Kupriyanova E. V., Protsykova M. A., Rakovskaia C.A., Slonova L.A.
Siberian Aerospace Academy
Krasnoyarsk State University
Krasnoyarsk State Trade-economic Institute
Russia, Krasnoyarsk
THE IDENTIFICATIN OF MULTIPLY CONNECTED SYSTEMS UNDER INCOMPLETE INFORMATION
Annotation. The problems of interconnected stochastic systems identification in the broad sense are considered in the work. In addition the priory information about the parametric model structure is absent. Under these conditions the nonparametric modeling occurs to be perspective.
Красноштанов А. П., Куприянова E. В., Процыкова M. А., Раковская С. А., Слонова Л. А.
Сибирская Аэрокосмическая Академия
Красноярский Государственный Университет
Красноярский Государственный Торгово-экономический Институт
Россия, Красноярск
ИДЕНТИФИКАЦИЯ МНОГОСВЯЗНЫХ СИСТЕМ ПРИ НЕПОЛНОЙ ИНФОРМАЦИИ
Аннотация. В работе рассматриваются задачи идентификации взаимосвязанных стохастических систем в широком смысле. При этом априорная информация о параметрической структуре модели отсутствует. В этих условиях перспективным оказывается непараметрическое моделирование.
Let ![]() be the vectors of
observed random sequences representing accordingly output
be the vectors of
observed random sequences representing accordingly output ![]() and input
and input ![]() variables
of the analyzed process. Let's define the function of solutions
variables
of the analyzed process. Let's define the function of solutions ![]() as some function representing the output of the adaptive system in
the influence
as some function representing the output of the adaptive system in
the influence![]() .
.
For the open scheme, shown in the figure 1, following variables are
introduced ![]()
which are observed in discrete moments of time ![]() of finite or infinite size
of finite or infinite size![]() .
.
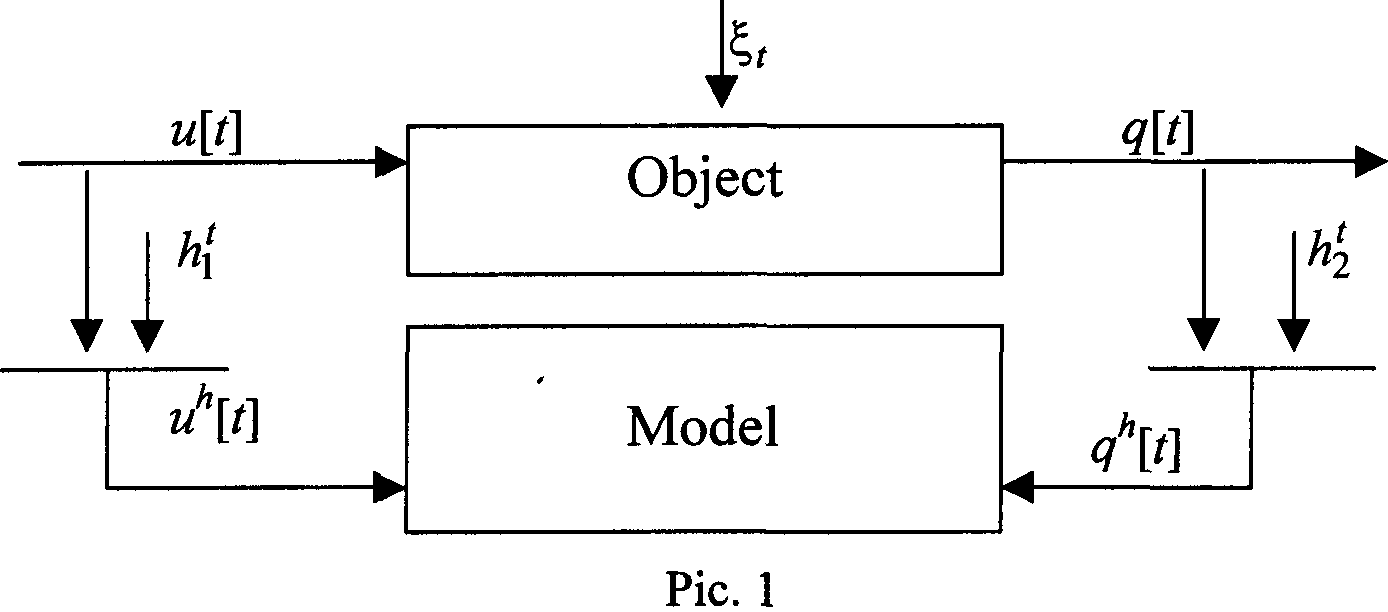
Further index ![]() in
observed variables is omitted because of the simplicity reason. The noise
in
observed variables is omitted because of the simplicity reason. The noise ![]() and
and![]() , are such, that
, are such, that ![]() Let's
form the optimum criterion
Let's
form the optimum criterion![]() where
where ![]() is some convex function. The problem of
searching of the best
is some convex function. The problem of
searching of the best ![]() amounts to the
amounts to the ![]() minimization with respect to
minimization with respect to ![]() that is the search if such
that is the search if such![]() that
that![]() It's clear that the form of
It's clear that the form of ![]() will
be determined be the form of function
will
be determined be the form of function![]() .
If
.
If ![]() then
then
![]() (1)
(1)
We also may consider other types of ![]()
Further the problem is in estimating ![]() by the observations
by the observations![]() which are
formed out of the initial samples
which are
formed out of the initial samples ![]() The sign
The sign ![]() denotes the time vector.
denotes the time vector.
With the passive information accumulation, i.e. in the presence of the
sample![]() the nonparametric estimating
algorithm (1) is :
the nonparametric estimating
algorithm (1) is :
![]() (2)
(2)
where the matrices ![]() are such, that
are such, that ![]()
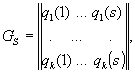
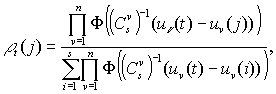
Where T- transpose sign.
While constructing the model of some object the problem is in finding
the estimate of ![]() function describing the
object's behavior. This estimate is usually found by using the mean square optimum
criterion.
function describing the
object's behavior. This estimate is usually found by using the mean square optimum
criterion.
It's clear that the ![]() estimate
error mean square will be minimal if to take
estimate
error mean square will be minimal if to take ![]() as the mean of the random value
as the mean of the random value ![]() in the given
in the given ![]() i.e.
i.e. ![]() represents the regression.
represents the regression.
The construction of the regression models gives a good result in case
of symmetric conditional probability densities, as since the mean value of ![]() practically coincides the most probable one. If
the probability distribution has the brightly expressed asymmetric character then it is
better to use the probability models. As the function
practically coincides the most probable one. If
the probability distribution has the brightly expressed asymmetric character then it is
better to use the probability models. As the function ![]() is the optimum criterion we'll take
is the optimum criterion we'll take![]() where
where ![]() , -the Dirac
delta-function. After the minimization of this criterion with respect to
, -the Dirac
delta-function. After the minimization of this criterion with respect to ![]() we get the mode of conditional probability
density
we get the mode of conditional probability
density![]() , i.e.
, i.e.
![]() (3)
(3)
As it is known the nonparametric estimate of conditional probability density is the estimate
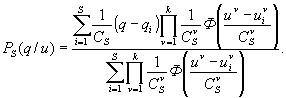 (4)
(4)
Where the kernels ![]() are
symmetric, delta-like for
are
symmetric, delta-like for ![]() functions with
properties of probability density at the set
functions with
properties of probability density at the set ![]()
It's important from the practical point of view to analyze the regression models in nonstationary (unstable) conditions. It's assumed that the probabilistic characteristics of an object are changing during the time in unknown way. The nonparametric estimate of regression function which looks like:
![]()
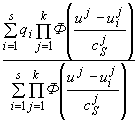 (5)
(5)
and it should be modified by putting the additional weights - some kind
of "memory functions", decreasing with the ![]() increase. Ibis fact corresponds to "forgetting" the old information.
increase. Ibis fact corresponds to "forgetting" the old information.
Essential interest, from the practical point of view, represents the
case when for some relations between the vector components ![]() and
and ![]() the parametric
relation is known up to the set of parameters
the parametric
relation is known up to the set of parameters ![]() , and other relations are unknown. In this situation we collide with
the problem of identification which doesn't correspond neither to the parametric nor to
the nonparametric level of priory information. These models arise when describing the
complex interconnected processes (often this situation arises while modeling of
manufacturing processes with the continuous technology) and has a form of an iterconnected
system:
, and other relations are unknown. In this situation we collide with
the problem of identification which doesn't correspond neither to the parametric nor to
the nonparametric level of priory information. These models arise when describing the
complex interconnected processes (often this situation arises while modeling of
manufacturing processes with the continuous technology) and has a form of an iterconnected
system:
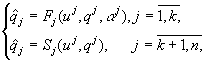 , (6)
, (6)
where the index ![]() at the
arguments
at the
arguments ![]() denotes the definite (the
denotes the definite (the ![]() -th) set of these components out of all
components,
-th) set of these components out of all
components, ![]() —
—![]() -th parametric model,
-th parametric model, ![]() - nonparametric (the
- nonparametric (the ![]() -th)
model,
-th)
model, ![]() -the vector of the output variables
of the model,
-the vector of the output variables
of the model, ![]() - the vector of the input
variables,
- the vector of the input
variables, ![]() -the parameters estimate.
-the parameters estimate.
The combined nonparametric models in the class of H-models look like
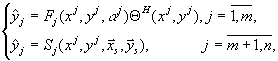 (7)
(7)
where ![]() the sample of
statistically independent observations
the sample of
statistically independent observations ![]() of
size
of
size ![]() at the domain
at the domain ![]() of the set
of the set![]() . While
using the H-models (7) the defects which are possible while using the models (6) are
excluded. It's clear that if
. While
using the H-models (7) the defects which are possible while using the models (6) are
excluded. It's clear that if![]() then the
models (7) transfer to the models (6). The set
then the
models (7) transfer to the models (6). The set ![]() is called the domain of technological rule.
is called the domain of technological rule.
Let the manufacturing process be some aggregate of interconnected
technological devices (objects), which models we'll denote as ![]() where
where ![]() -accordingly
output and input variables of the
-accordingly
output and input variables of the ![]() -st
object,
-st
object, ![]() -the parametric relation
-the parametric relation ![]() on
on ![]() , up to parameters
, up to parameters ![]() and
т - the number of objects. In case if all models are constructed (some models can
be the models of nonparametric type), then the problem of model construction of the whole
complex often arises. It's natural to use for mis purpose the models of local objects
and
т - the number of objects. In case if all models are constructed (some models can
be the models of nonparametric type), then the problem of model construction of the whole
complex often arises. It's natural to use for mis purpose the models of local objects ![]() of the type (6), (7). But arithmetic
"assembling" of these models as the rule doesn't provide the desired accuracy.
In techniques the analog of this fact is the assembling of some article of separate blocks
each one of which satisfies the technical conditions but the functioning of the whole
article doesn't satisfy the according technical specifications and that's why the
necessity of the adjustment of the whole article arises, which represents the simultaneous
adjustment of all or some local blocks. The process of "assembling" of the
macro-model out of local ones and their following " adjustment" we called the
models macro-synthesis.
of the type (6), (7). But arithmetic
"assembling" of these models as the rule doesn't provide the desired accuracy.
In techniques the analog of this fact is the assembling of some article of separate blocks
each one of which satisfies the technical conditions but the functioning of the whole
article doesn't satisfy the according technical specifications and that's why the
necessity of the adjustment of the whole article arises, which represents the simultaneous
adjustment of all or some local blocks. The process of "assembling" of the
macro-model out of local ones and their following " adjustment" we called the
models macro-synthesis.
LITERATURE
1. Medvedev A.V. Nonparametric adaptation systems. Novosibirsk: Nauka 1983
2. Tarasenko F.P. Nonparametric statistic. Tomsk: TGU, 1976.
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|