 |
||
Vladimir D. Noghin
Russia, St.-Petersburg, Department of Mathematics, St.-Petersburg State Technical University
E-mail: noghin@osipenko.stu.neva.ru
RELATIVE IMPORTANCE OF CRITERIA IN A FUZZY CASE
Abstract. Elements of quantitative theory of relative importance of criteria in case of fuzzy preference relation are presented. The basic mathematical definition of relative importance of criteria generalizes one, introduced by the author in nonfuzzy case. The main result of the pa- per contains an upper estimate for unknown fuzzy set of non-dominated vectors.
Владимир Д. Ногин
Россия, Санкт-Петербург, кафедра математики СПбГТУ Эл. почта: noghin@osipenko.stu.neva.ru
ОТНОСИТЕЛЬНАЯ ВАЖНОСТЬ КРИТЕРИЕВ В НЕЧЕТКОМ СЛУЧАЕ
Аннотация. Представлены элементы теории относительной важности критериев в случае нечеткого отношения предпочтения. Основное математическое определение относительной важности обобщает определение, введенное автором в четком случае. Главный результат работы содержит оценку сверху для неизвестного нечеткого множества недоминируемых векторов.
1. INTRODUCTION. Usually a decision-maker (DM) possesses certain information on relative importance of criteria. A lot of authors characterize the importance of criteria by means of special positive numbers called importance coefficients. These authors do not try to give any rigorous definitions for the coefficients. As a rule, each author proposes his own procedure to obtain the coefficients and different procedures lead to distinct results. They are interested in obtaining the coefficients but they do not analyze the nature of the relative importance.
What do we mean by "criterion i is more important than criterion] "? How may we use a numerical information on relative importance of criteria when a fuzzy preference relation of the DM is unknown?
This paper being an extension of[1] deals with problems relating to above questions. We shall give a formal definition of the concept of relative importance in a fuzzy case and formulate new original results to construct an upper estimate for a fuzzy set of non-dominated vectors. Some examples illustrate the theoretical results.
2. NOTATION AND PRELIMINARY DEFINITIONS. Let ![]() be an т –dimensional vector space,
be an т –dimensional vector space, ![]() .
.
Recall that a map m : ![]() is called a (binary) fuzzy relation. A
fuzzy relation m (· ,· ) are said to be
is called a (binary) fuzzy relation. A
fuzzy relation m (· ,· ) are said to be
• irreflexive, if ![]()
• asymmetric, if ![]() implies
implies ![]()
• transitive, if ![]()
• invariant with respect to positive linear transformation, if ![]()
for any. ![]()
Let m be a fuzzy relation. The relation m is called a (fuzzy) cone relation, if there exists a fuzzy
cone l : ![]() (i.e.
(i.e. ![]() for all
for all ![]() ), such that
), such that ![]() for any
for any ![]() .
.
We shall use superscripts to indicate the vector and subscripts to indicate the components of such vector.
3. BASIC DEFINITIONS. Consider a mathematical model of choice
consisting of the three objects ![]() ,
where
,
where ![]() is a number of criteria, m :
is a number of criteria, m : ![]() is an asymmetric
fuzzy relation of the DM,
is an asymmetric
fuzzy relation of the DM, ![]() is a
set of feasible vectors.
is a
set of feasible vectors.
If ![]() is preferred
to
is preferred
to ![]() with respect to the i-th
criterion (i.e.
with respect to the i-th
criterion (i.e. ![]() ), then the positive number
), then the positive number
![]() indicates a "degree" of the
preference.
indicates a "degree" of the
preference.
Further we shall suppose the fuzzy relation m
satisfies Pareto axiom, i.e. for all ![]()
![]()
imply ![]() .
.
Definition 1. Let ![]() . A
criterion i we shall call more important than a criterion j with two given
positive parameters
. A
criterion i we shall call more important than a criterion j with two given
positive parameters ![]() and a grade of
confidence
and a grade of
confidence ![]() , if for all vectors
, if for all vectors ![]() relations
relations
![]()
![]()
imply ![]() . The
number
. The
number
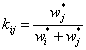
is called a coefficient of relative importance.
Example. Let т =3. Assume that the first criterion is more
important than the second one with the coefficient ![]() and
and ![]() . Then, for instance, the
vector
. Then, for instance, the
vector ![]() is more preferred than
is more preferred than ![]() and also
and also ![]() , because of
, because of![]() ,
, ![]() and
and ![]() .
.
4. USE OF INFORMATION ON RELATIVE IMPORTANCE. As above let Y ![]() be a set of feasible vectors and m :
be a set of feasible vectors and m : ![]() be an asymmetric
fuzzy relation (which as a rule in practice is unknown). The fuzzy set whose a membership
function is
be an asymmetric
fuzzy relation (which as a rule in practice is unknown). The fuzzy set whose a membership
function is
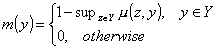
is called a fuzzy set of non-dominated vectors [2]. This notion is an extension of well-known concept of (non fuzzy) set of non-dominated vectors [3].
Theorem 1. Let p. be an irreflexive transitive and invariant
fuzzy relation, which satisfies Pareto axiom. Suppose that a criterion i is more important
than a criterion j with a coefficient of relative importance ![]() and a grade of confidence
and a grade of confidence ![]() . Then
. Then
![]() (1)
(1)
where M is a membership function of a fuzzy set of non-dominated vectors with respect to the fuzzy relation l :

Here ![]()
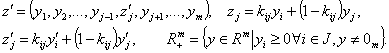
The inequality (1) shows that a fuzzy set with the membership function т is a subset of the fuzzy set with the membership function M, i.e. the second set is an upper estimate for the first one. Thus, when the fuzzy preference relation p, is unknown, due to Theorem 1 we may construct an upper estimate M(y) for a fuzzy set of non-dominated vectors m(y) using in- formation on relative importance of criteria.
5. EXAMPLE. Let ![]()
![]() . Evidently, in this case a Pareto set is
. Evidently, in this case a Pareto set is ![]() , since
, since ![]() .
.
Suppose that we have got an additional information on relative
importance of criteria. Namely, the first criterion is more important than the second one
with the coefficient ![]() and the grade of
confidence
and the grade of
confidence ![]() . Then in according to Theorem 1
we have
. Then in according to Theorem 1
we have
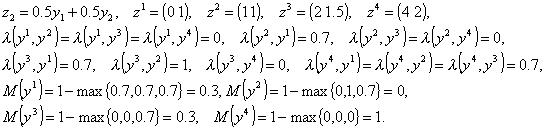 Hence, in this case
the fuzzy set of non-dominated vectors is given as follows
Hence, in this case
the fuzzy set of non-dominated vectors is given as follows
![]()
It is an upper estimate for the unknown fuzzy set of non-dominated vectors with respect to preference relation m . It is easy to see that the vector y4 is the most preferable for the DM in according to the additional information on relative importance of criteria.
6. GENERAL CASE. In a general case let us introduce the following definition.
Definition 2. A group of criteria ![]() we shall call more important than a group of criteria
we shall call more important than a group of criteria ![]() , with given positive parameters
, with given positive parameters ![]() (for all
(for all ![]() ),
), ![]() (for all
(for all ![]() ) and a grade of confidence, if for all
) and a grade of confidence, if for all ![]() relations
relations
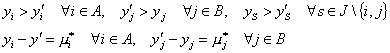
imply ![]() .
.
As above the number ![]() we
shall call a coefficient of relative importance for all
we
shall call a coefficient of relative importance for all ![]() and
and ![]() .
.
It can be proved the following result.
Theorem 2. Let m be an
irreflexive transitive and invariant fuzzy relation, which satisfies Pareto axiom. Suppose
that a group of criteria A is more important than a group of criteria В , with the
coefficients of relative importance for all ![]() ,
, ![]() and a grade of
confidence
and a grade of
confidence ![]() . Then
. Then
![]()
where M is a membership function of a fuzzy set of non-dominated vectors with respect to the fuzzy relation l :

with ![]() and
and ![]() . Here the first
. Here the first ![]() components of the vector z are
components of the vector z are ![]() and tne otner components are
and tne otner components are ![]() for all
for all ![]() ,
, ![]() (similarly for the vector
(similarly for the vector ![]() ).
).
Corollary. By hypotheses of Theorem 2 the maximal value of p is attained in the case
![]()
Here the brackets [![]() ]
denote an integral part of number
]
denote an integral part of number ![]() .
.
For example, if ![]() ,
then p = 10 - 5 + 25 = 30. Thus, in order to construct an upper estimate for a
fuzzy set of non-dominated vectors, when a group consisting of five criteria is more
important than other group consisting of five criteria, in according to Theorem 2 we have
to deal with a mathematical model which contains thirty criteria and also twenty five
among of them are new.
,
then p = 10 - 5 + 25 = 30. Thus, in order to construct an upper estimate for a
fuzzy set of non-dominated vectors, when a group consisting of five criteria is more
important than other group consisting of five criteria, in according to Theorem 2 we have
to deal with a mathematical model which contains thirty criteria and also twenty five
among of them are new.
REFERENCES
[1] Noghin, V.D. (1997), Relative importance of criteria: a quantitative approach. Journal of Multi-Criteria Decision Analysis, 6, pp. 355-363.
[2] Orlovsky, S.A. (1978), Decision making with a fuzzy preference relation. Fuzzy Sets and Systems, 1,pp. 155-167.
[3] Yu,P.L. (1985), Multiple-Criteria Decision-Making: Concepts, Techniques, and Exten- sions, New-York: Plenum.
[4] Noghin, V.D. (1994), Upper estimate for a fuzzy set of nondominated solutions. Fuzzy Sets and Systems, 67, pp. 303-315.
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|