Russia, Самара, Samara state technical university, nova@mail.samtel.ru

The known method of piecewise linear approximation is applied for identification of nonlinear dynamic models. However, the basic attention is given to a question of reception of consistent ratings for a case of presence autocorrelation noise in the form martingale differences, for models described with linear different equations. The original generalized method of the least squares is applied , it helps to receive consistent ratings of parameters of linear difference equations under weak restrictions on the input signal and hindrance.

Россия, г. Самара, Самарский государственный технический университет, nova@mail.samtel.ru

Для идентификации нелинейных динамических моделей применен известный метод кусочно-линейной аппроксимации. Однако, основное внимание уделяется вопросу получения состоятельных оценок для случая наличия автокоррелированного шума в форме мартингал разностей, для моделей, описываемых линейными разностными уравнениями. Применен оригинальный обобщенный метод наименьших квадратов, с помощью которого при слабых ограничениях на входной сигнал и помеху удается получить состоятельные оценки параметров линейного разностного уравнения.

The report is concerned with regression models, which though are nonlinear functions within a whole allowable area of change of the input variables, but the approximation is possible with their linear functions within the limits of separate sub areas of input space.

The basic feature of each of sub areas of change of the input variables is the availability of auto correlated noise in the observation channel, the model is being set in the form of linear difference equation.

Description of dynamic objects with linear difference equations depends on a point of application of a hindrance. A hindrance is being available at the input of the direct channel (before the operator of a feedback channel of use of usual procedure of method of least squares (МLS) allows to receive strongly consistent estimates under rather weak restrictions to an input signal and hindrance. But in case an additive hindrance is applied in the output channel of object the task of identification becomes already the task of regression analysis with mistakes in independent variables; thus the estimates of parameters received with usual MLS will be inconsistent , even if a hindrance is a stationary discrete white noise.

The report describes the algorithm of nonlinear МLS for identification of parameters of linear difference equations under additive locally auto correlated noise in the observation channel . The strong consistency of offered estimates is proved under conditions to an input signal and hindrance. The questions of existence of these estimates are being considered . The proof of strong consistency is based upon the theorem of convergence of martingale and Kronecker’ s lemma .

Let us consider the stationary dynamic system, described with the following linear difference equation of the given order with discrete time

(1)

and output variable is observed with additive noise as

(2)

where - operator of delay;

and- observable input and output signals accordingly;

- unobservable output signal;

- unobservable noise;

- unknown material true value of parameters.

1). The stochastic process satisfies the conditions:

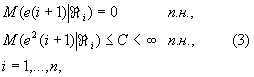
where - conditional mathematical expectation;

algebra, induced by the class of random variables set of integers

2). The following conditions are met :

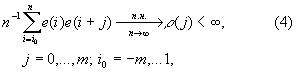
where local autocovariation function.

Matrix

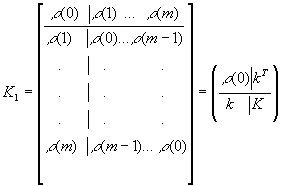
Positively determined, where т- transposition mark, and matrix K:

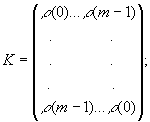
vector .

3). Random variables does not depend upon

4). The true value of parameters satisfy stationary state conditions, i.e. roots of the characteristic equation

lay outside a unit disk.

5). The input signal is a random process and satisfies the conditions of constant excitation of the order q, i.e. with probability 1 exists

and matrix positively determined, where - set of rectangular material matrixes of dimension (q+1)(q+1);

Let a stationary dynamic system is described by the equations (1), (2) and the hindrance satisfies the assumptions (3) - (5).

Then at with probability 1 there is an estimate

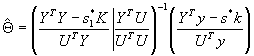
where - the least root of the equation

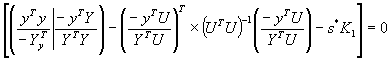and

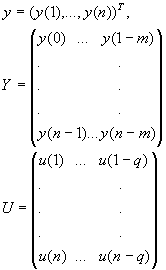
thus the estimation - is strong solvent. In the report are given the software and tests.