Bulgaria, Sofia 1113, acad. G. Bonchev Str. Bl. 29A, IIT-BAS. Email: vsjotsov@yahoo.com

Abstract. The defeasible reasoning is applicable in situations when exclusions from the used rules could appear, aiming at defeating some of the existing knowledge. Defeasible analogies shorten the process of searching for and applying such knowledge. Their application decreases the complexity of the inference problem as a whole. The paper discusses a special knowledge representation in the network flow form applied especially for defeasible analogies purposes. This allows to combine logical and quantitative approaches, and to obtain the advantages from both of them.

Болгария, София, ИИТ-БАН, ул. Акад. Г. Бончева, Бл. 29А.

Аннотация. Аннулирующий вывод применяется в ситуациях, когда появляются исключения из правил с целью аннулирования существующих знаний. Для сокращения времени поиска подобных исключений предложено использовать аннулирующие аналогии. В докладе предлагается использовать потоки в сетях для целей аннулирующего вывода по аналогии.

1. INTRODUCTION

In the general case every rule can be represented by the help of a relation of the type "B follows from A": A® B, where B is a statement from the rule head, A is the body of the rule. When an "exclusion from the rules" E(C,A) is applied to statement A, the reason-sequence relation is altered. D. Note introduces in [1,2] the notion defeasible inference on the basis of the use of exclusions, attached to one or to a group of rules or separate statements (facts). Defeasible inference is expanded as a notion and application in papers [3, 4] in the following way.

2. PURPOSE AND INVESTIGATION PROBLEMS

It will be pointed below that the operation mechanisms of the exclusions from the rules can be realised in a different way, which changes the results from logical inference. Thus several different types of defeasible reasoning have been formulated. Let a rule of Horn's type (1) be given:

(1)

where A_i are conjuncts from the rule body (I={1, 2, ..., z}, (the conjunction will be further denoted by the symbol C only for the union of conjuncts from the antecedents of the rules), and B is one statement - head of the rule (it is a result of the relation). When applying two-valued logics to artificial intelligence (AI) problems, if at least one statement from A_i is not true, then B is not defined (true or false). In case an appropriate exclusion from rule (1) is found (the notion exclusion only will be used further on) in connection with any A_p (it is assumed that pI I), the procedure for inference changes. In case the exclusion E(C, A_p) and C are true and A_p is false, then B can be true (by exception). In [3, 4] extended models of defeasible inference are suggested, generalised in the paper in a formalised type (3), (2)-(4) and/or (2)-(5).

(2)

(3)

(4)

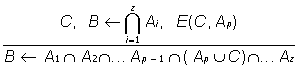(5)

where a _i are apriori given coefficients of the significance of statements - conjuncts from the antecedents of the rules (the term belief is also used for them). It is seen from the formulas that the exclusions are also a kind of connection of a rule relation character, and their area of operation includes one or more rules (1). The exclusions may be distributed among the objects studied by inherited properties in a connection of ancestor-predecessor type. The defeasible reasoning proposed in (3) is based on the following. If there exists an exclusion E(C, A_p) connected with one of the rules with a head B and as a result of its action A_p is obtained, then the conjunct A_p from the rule body is replaced by O A_p. In case C is not true, the corresponding replacement is not executed. When applying Modus Ponens, the juxtaposition between B and O A_p leads to a formal logical contradiction. There is not such a contradiction when using the respective exclusion and the Modus Ponens rule. Hence, the formation of exclusions of E(C, A_p) type can lead to solution of the contradictions caused by incompleteness in the description of the object area.

In case C from formula (4) is true and exclusion E(C, A_p) connects it with the conjunct A_p, the significance of the last falls to zero. As a result of the defeasible reasoning considered, A_p is eliminated from the body of the respective rule of type (1), since its validity value does not influence the inference process of B. In the last variant of defeasible reasoning (5), when C is true, the respective conjunct A_p is directly replaced by C under the action of the exception E(C, A_p) attached to the rule.

If there are not any data for the coefficients pointed in (2), their values are accepted as equal. The general inference is made from scheme (4) that no matter whether the presence of reason C leads to A_p or O A_p, it causes the defeasibility! of the significance of the statement A_p confirming B, a _p=0 at that. Each one of the exclusions E(Cn ,A_p) considered can be replaced by the disjunctive expression (Cn E A_p).

The papers discussed suggest the use of an approach for defeasible reasoning in the formation of exclusions E(Cn ,A_p). In this way the combinatorial explosion in the search of all the exclusions for the statements from all the rules is avoided and more attention is paid to some definite situations leading to the activation of such analogies. One of the problems which appear is to represent a formal apparatus for defeasible reasoning on the basis of the known approaches for detection of partial similarities between different models [5]. The types of defeasible reasoning are discussed in detail in the next chapter. The application of defeasible type analogies increases the efficiency of the search and application of exclusions. Independently on these facts other (quantitative) methods have been investigated that enable a rise in the efficiency of these tools application and the removal of many shortcomings, typical for the non-quantitative methods.

Different models [6] are used in exact quantitative methods based on linear equalities and inequalities designed for the solution of various problems in connection with deductive logic. For this purpose a method is suggested in this paper for defeasible reasoning by analogy using flows on networks. In this case the choice of the most appropriate hypothesis is reduced to solving the corresponding network-flow optimisation problem, discussed in the third chapter.

3. DEFEASIBLE REASONING BY ANALOGY

The inference by analogy is based on the analysis of a partial similarity among the models investigated. Further on the clauses of Horn's type are called rules, and the statements C; A_i - facts. Let us consider different objects of the investigation from a defined object area (the approach suggested is object-independent). The set of rules and facts, concerning a given object X, form its model: M(X). This model is identified with Herbrand model, and the object area - with Herbrand Universe. All the well formed formulas (facts) from M(X) are logical sequences of X. The analogy is based on juxtapositions and comparisons among different objects. The paper studies comparisons between models of some pairs from the set of objects: X₁, X₂. The purpose of transformation (the area, to which new knowledge is added), is connected with the object X₁, and the transformation basis (the area, in which appropriate exclusions are searched for) - with X₂. The comparisons must have mutually excluding character: two facts from M(X₁) cannot correspond to one fact from M(X₂) and vice versa. In the replacement of the variables by constants particular attention is paid to the excluding of uncertain factors. The features mentioned give the necessary but not sufficient conditions for inference by defeasible analogy.

Definition. Let us consider M(X₁). Defeasible analogy is the approach enabling the transfer by analogy of exclusions of the type C ® A_p, included in the models of other objects M(X_j) and on the basis of sufficient partial similarity between the objects X₁ and X_j, exclusions are added to M(X₁). The same can change the deductive inference using defeasible reasoning (3), (4) or (5). Another type of defeasible reasoning allows forming by analogy (without direct transfer from other objects) of exclusions of the type C ® A_p.

It is necessary to note the absolute difference between our background definition for defeasible analogies and the defeasible reasoning of D. Note. In our case, if the exclusion considered E(C,A_p) concerning one message A_p is true and its area of operation covers the rule R_i, containing A_p in its head or body, then A_p is defeated. Hence, without altering the truth value of A_p, its connection with R_i changes in the following way. In the critical case the connection A_p-R_i is interrupted: The significance of the information whether A_p is true or false becomes null in connection with the truth value of R_i. From the schemes above shown it follows that A_p can be simply cleared from the rule or replaced by another coincidence. The connection A_p-R_i is altered in the general case. The change affects the significance of the fact whether A_p is true or not within the frames of the complete rule. The significance increases in some cases on the account of other messages, if there are such. In other cases it decreases, not obligatory to zero. Thus something similar to scales is introduced for the head and the body of R_i, on which the changes in the weight of one or a group of statements in connection with R_i are fixed. Finally this can change the truth value of R_i.

The exclusions can be specialised for one or a group of statements of one or more rules or for all the known rules of the domain. The paper discusses the different partial cases of the defeasible reasoning suggested by us. The discussion is restricted within the frames of Horn’s clauses, and the position of A_p is in the rules body.

Let us regard a rule of the type B ¬ A₁ C A₂ ... C A_z, assigning each A_i the corresponding a _i. Also, let the knowledge leading to the confirmation of any statement in A_i be called examples for B (because they do not support the confirmation of B). Similarity can be found with machine learning terms, for example. The knowledge leading to O A is called counterexamples for B. Then if C is true, the application of the exclusion C ® A_p alters the ratio between the examples sets and the counter examples for B, because A is eliminated in one of them. If the result of this is that one of the sets remains empty, the deductive inference is altered. The defeasible analogy is used with the purpose to eliminate the elements in one of the two sets and to change deductive inference. Usually it is described by formula (6), but the mechanism for exclusions application can be in three variants, that are formalised in (3), (4) or (5).

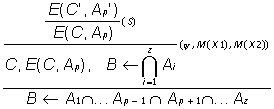(6)

where S is the substitution mentioned at the beginning of the chapter, allowing the use of the exclusions available connected with other objects in M(X₁). If there is such a substitution in the upper line of (6), then exclusion transfer is realised (refer to the intermediate line in the formula) from M(X₂) in M(X₁). After the lowest line of inference in (6), the results from the use of the defeasible process C ® A_p in M(X₁) are pointed out. Four variants for the formation of y are investigated so that they can be used in a combination or apart. Independently on the variant selected, if the y (X₁,X₂)<T obtained is smaller than an apriori given value T, the hypothesis formed by analogy is rejected.

One of the most simple and efficient procedures in a computing complexity aspect for the formation of y is based on the estimate of the distance between X₁ and X₂ in the hierarchical network of objects. For this purpose relations ancestor-predecessor are used that are described in properties acquisition in deductive inference. Let each relation be interpreted by an arc with length 1, at the upper end of which a predecessor! is placed and at the lower - an ancestor. The neighbourhood (the distance) between the objects L(X₁,X₂) is computed in the following way. If X_1? X₂, then L(X₁,X₂) = 0 (maximal neighbourhood). In case X₁ and X₂ have a common predecessor, L(X₁,X₂) = 1 and so on. If X₁ and X₂ have not a common predecessor at any hierarchical level, then L(X₁,X₂) = ? . In the variant shown the analogies are done up to an apriori set value of L. The next chapter describes a scheme for defeasible reasoning by analogy, being described in the notions of deduction (Modus Ponens) and formalized by (7).

(7)

where E(C, A_p) is connected with X₂, and all the remaining statements - with X₁. Also, with the purpose to increase the efficiency of defeasible reasoning, it is suggested to use metacontrol of inference by analogy expressed in the use of analogies only in case that one of the sets of the examples and counter examples of the consequent of (1) contains no more than one element. It is suitable to make comparison between the defeasible reasoning suggested and other approaches for reasoning by analogy, at the first place the Haraguchi approach (refer to the first chapter). In order to discover the characteristic differences, it is sufficient to trace what the situation will be after the elimination of y from formula (6). In this case the analogy becomes practically uncontrollable and it cannot function in automatic mode of operation without an expert who has the task to remove the inconsistent hypotheses. The analogy described in one of the early works of Haraguchi is similar, being described in formal deductive inference notions.

4. FLOWS IN NETWORKS FOR INFERENCE BY ANALOGY

A flow interpretation of the inference is proposed in the present paper for formal defeasible reasoning using the terms from [7, 8]. Let the graph G(N,U) be given on a set of arcs U and nodes N. In this case the relation (7) can be represented as a network flow on graphs from Fig. 1.

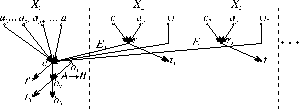
Figure 1.

The graph is divided by dotted lines into areas, each one containing knowledge about one object X_j. The set of sources S contains all A_i, the exclusions E, y _i. The set of sinks T contains all tn , t₀, and t’. Then for all X,yI N the constraints from expression (8) are valid.

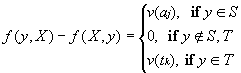(8)

A_i corresponds to the arc flow functions f(a_i,a); Cn , A_p and E(Cn ,A_p) - to f(c_i,r_i), f(a_p,r_i), f(r_i,a), respectively, and f(y _i,a) is assigned initially the value 1, if y (X_j,X₁)<T or 0 otherwise. Some appropriate exclusions E(Cn ,A_p), i? j can be included in the knowledge about an object X_j. The pairs of the incoming arcs are disjunctively joint in the nodes r_i, and in nodes a and b₂ - conjunctively. The functional relations v from formula (8) are formed as follows: v(a_j)=f(a_j,a); v(tj)=f(a,t_j).

Let the conjunction of all A_i, exclusions i, y _i be denoted by A, which corresponds to the arc (a,b₂). Then the implication A® B is set by the arc (b₁,b₂) and as a result of the deductive inference f(b₂,b₃) is computed, the value of which is a true estimate of B. Then the inference by analogy is represented by the following system of equalities and inequalities.

f(a,b₂)-f(a_i,a)? 0; i=1,...z. ( 9)

f(a,b₂)-f(r_j,a)? 0; j=1,...n. (10)

f(a,b₂)-f(r_j,a)? 0; j=1,...n. (11)

f(r_j,a)-f(c_j,r_j)? 0; j=1,...n. (12)

2f(r_j,a)-f(c_j,r_j)-f(a_p,r_1j)=0; j=1,...n. (13)

(14)

2f(b₂,b₃)-f(a,b₂)-f(b₁,b₂)=0. (15)

f(r_j,a) = 0 or 1. (16)

f(x,y)? 0; (x,y)I U. (17)

f(r_j,t_j)? 1. (18)

f(a,t’)? 2n+z-2. (19)

f(b₂,t₀)? 1. (20)

The equations for preserving are given by formulas (13)-(15), while the equations from (9) up to (12) guarantee that the conditions from the tables for the logical operations disjunction and conjunction are satisfied.

The problem for defeasible reasoning by analogy put is reduced to a linear programming problem from (9) up to (20) with the following objective function:

(21)

Fig. 1 shows one case of defeasibility of one of the conjuncts Ai by the antecedent of (1). In the general case several conjuncts can be defeated simultaneously, which leads to complication of the graphical representation and the system of formulas. As shown in chapter 1, this is not appropriate in most of the cases, since it can cause decrease of the efficiency in defeasible analogy application.

Similarly to the scheme for inference (7), scheme (6) is realised in a flow form of representation that leads to transformation of rules, but not to check of the probability value of statements as shown above. Usually all the modifications of exclusions from (3) up to (5) are used in the investigations, as well as an inference using efficiency coefficients (1). The modifications indicated do not alter the nature of the scheme for defeasible reasoning by analogy shown in Fig. 1.

5. CONCLUSIONS

The paper presented suggests a network flow approach for defeasible inference by analogy, as well as the possibilities for its application in artificial intelligence and decision support systems. The features and common characteristics of different types of defeasible reasoning are discussed.

A method is proposed in which the defeasible reasoning is done in a network flow form. In this approach the logical programming problems are reduced to the solution of the corresponding problems by exact quantitative methods. For this purpose linear network flow models are used and an extremal linear network problem is solved.

REFERENCES

1. Nute, D. Defeasible reasoning and decision support systems. - Decision Support Systems 4, 1988, 97-110.

2. Nute, D., R. Mann, B. Brewer. Using defeasible logic to control selection of a business forecasting method. Proc. of the 21th Hawaii Int. Conf. on System Science. IEEE Comp. Soc. Press, Washington, DC, 1988.

3. Jotsov, V. Defeasible reasoning by using analogies. In Proc. IV Int. Conf. AIMSA’90, edited by P. Jorrand and V. Sgurev. North- Holland, 1990, 285-292.

4. Sgurev, V., V. Jotsov. Computational analogy: some resultes and perspectives. - J. Probl. of Ind. Cybern. and Robotics 46, 1997, 12-20.

5. Haraguchi, M., S. Arikawa. Reasoning by analogy as a partial identity betwen models. - Lecture Notes in Computer Science 265, edited by K. Jantke, Springer, Berlin, 1986, 61-87.

6. Jeroslow, R. Logic-Based Decision Support. North-Holland, N.Y., 1986.

7. Sgurev, V.S., M.N. Djelatova. Maximal Linear Flow and Capacity of a Cutting Set. - Problems of Engineering Cybernetics and Robotics, 25, 1986, 3-10.

8. Sgurev, V.S. A Maximum Network Flow and a Capacity in Networks with Nonlinear Constrains. - Problems of Engineering Cybernetics and Robotics, 31, 1990, 18-22.