 |
||
ShanshiashviliB. G.
Georgia, Tbilisi.
Georgian Technical University.
Email: besoshan@hotmajl. corn
IDENTIFICATION OF LINEAR DYNAMICAL SYSTEMS WITH TIME-VARYING PARAMETERS
Abstract. Parameter identification of the linear dynamical systems with time-varying parameters, in case of some restrictions of system's input and output variables and parameters is given. The problem of identification as inverse problem of solution of ordinary linear differential equation with variable coefficients is considered. It is proved theorem about existence of such interval, where the algorithm of the identification of parameters is right.
Шаншиашвили В.Г.
Грузия, Тбилиси.
Грузинский технический университет.
Email; besoshan@hot.mail. corn
ИДЕНТИФИКАЦИЯ ЛИНЕЙНЫХ ДИНАМИЧЕСКИХ СИСТЕМ С ПЕРЕМЕННЫМИ ПАРАМЕТРАМИ
Резюме. Рассматривается задача идентификации параметров линейных динамических систем с переменными параметрами при некоторых ограничениях на входные и выходные переменные и параметры системы. Задача идентификации ставится как обратная задача решения обыкновенного дифференциального уравнения с переменными коеффициентами. Доказывается теорема существования интервала идентификации.
INTRODUCTION
In practice of automatic control linear dynamical systems with time - varying parameters are spread in large. Solution of problems of such system's identification is complicated that mathematical difficulties, which are meeted with solution differential equations with variable coefficients. In particular, by solution of non-homogeneous equations is necessary to known system of fundamental solutions of corresponding to its homogeneous equations, what isn't possible in most cases for real systems. In spite of that there are enough number of papers devoted to the identification of non-stationary systems, in which problems of the identification are solved by different approaches: for instance, by algorithms with approximation by linear combinations of known basic functions [1], by different modification of recurrent Least Mean Squares identification techniques [2], by Kalman filtering [3], by recurrent Bayesian algorithms [4] and others.
This paper dedicates to investigation of the identification of Imear dynamical systems with time - varying parameters. It means, that it is known structure of system's model. In this case problem of the identification consist in estimation of equations coefficients. Problem of system parameter estimation is considered as inverse problem of solution of ordinary differential equation with variable coefficients, when we have some restriction of system's input and output variables and parameters.
PARAMETER IDENTIFICATION OF LINEAR SYSTEMS
Let's consider multidimensional observed control system with n inputs and n outputs, which is described by following system of normal differential equations
![]() (1)
(1)
where ![]() and
and ![]() are system's input and output vectors,
are system's input and output vectors, ![]() and
and ![]() are n dimensional quadratic matrices of coefficients.
are n dimensional quadratic matrices of coefficients.
In this paper the problem of identification is considered in the
following way: according to the identification theory [5], as a result of system's input
and output variables observation we found that input variable ![]() and output variables
and output variables ![]() , which are solution of the system (1) with different initial state,
and also is known matrix
, which are solution of the system (1) with different initial state,
and also is known matrix ![]() , where R
is set of real numbers,
, where R
is set of real numbers, ![]() - interval,
- interval,
![]() ,
, ![]() and
and ![]() - sets of
continuous and continuous differentiable
- sets of
continuous and continuous differentiable ![]() functions correspondingly,
functions correspondingly, ![]() - set of n
dimensional real quadratic matrices,
- set of n
dimensional real quadratic matrices, ![]() - set
of all continuous
- set
of all continuous ![]() matrices. It is
required to determine unknown continuous matrix
matrices. It is
required to determine unknown continuous matrix ![]() , it means, that it is unknown system of fundamental solutions of
system homogeneous equations
, it means, that it is unknown system of fundamental solutions of
system homogeneous equations
![]() (10)
(10)
which corresponds to system (1).
Because ![]() is solution of
system (1), we have
is solution of
system (1), we have
![]() (2)
(2)
where
![]()
![]()
Let's introduce matrix ![]() ,
which columns of which are
,
which columns of which are ![]() :
:
![]() and matrix
and matrix 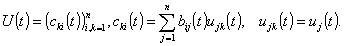
Then we can rewrite system (2) like matrix algebraic equation
![]() (3)
(3)
For determination matrix A(t) from (3) it is sufficient, that X(t) matrix is non-degenerated.
Let's show, that there exists such ![]() , that
, that ![]()
Theorem. If ![]()
![]() and
and ![]() , than there exists interval
, than there exists interval ![]() such that
such that ![]() , and in
, and in ![]() matrix A(t) is determined single-valued
matrix A(t) is determined single-valued
![]() (4)
(4)
Really, let's admit, that ![]() is solution of system (1) with
is solution of system (1) with
![]() (5)
(5)
initial condition.
It is known, that solution of problem (1), (5) defined by Cauchy formula [6]
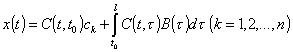 (6)
(6)
where ![]() matrix function
is Cauchy's matrix of system homogeneous equations (1o).
matrix function
is Cauchy's matrix of system homogeneous equations (1o).
In role of constants ![]() we take linearly undependent vectors, in particular:
we take linearly undependent vectors, in particular:
![]() (7)
(7)
where ![]() - is Kronecker's
symbol.
- is Kronecker's
symbol.
If we consider definition of Cauchy's matrix, we receive
![]() (8)
(8)
where E - is unity matrix.
Because X(t) is continuous matrix and determinant of continuous
matrix is continuous function, therefore there exists interval ![]() , such that
, such that ![]() and
and
![]() . Therefore for
. Therefore for ![]() there exists inverse matrix and matrix A(t)
can be determined by formula (4).
there exists inverse matrix and matrix A(t)
can be determined by formula (4).
This determination is single-valued because problem of Cauchy (1),(5)
for ![]() has unique solution according to
uniqueness and existence theorem.
has unique solution according to
uniqueness and existence theorem.
IDENTIFICATION OF PRACTICAL SYSTEMS
Assume that a system with two inputs and two outputs is described by system of differential equations
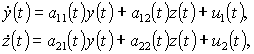 (9)
(9)
where
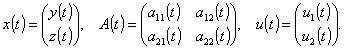
Suppose that after input-output system observation it is recieved:
![]() (10)
(10)
Form ![]() matrix
matrix
![]() (11)
(11)
Its determinant is
![]() (12)
(12)
It is clear, that ![]() ,
when
,
when ![]() . So
. So
![]() (13)
(13)
If calculate A(t) matrix by (4) we receive
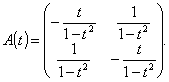 (14)
(14)
Thus, unknown system is
![]()
![]() (15)
(15)
The system of fundamental solutions of system homogeneous equations, which corresponds to system (15), is
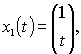
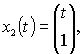 (16)
(16)
and fundamental matrix
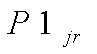 (17)
(17)
Because ![]()
![]() , therefore it is clear, that
, therefore it is clear, that
![]() (18)
(18)
and in this case ![]() .
.
Thus, for identification of real system, when structure of model is
known, we observe system's input and output with different initial states of system. Data,
received by observation, we make approximation with continuous functions. Then we compose ![]() matrix and in this interval, where determinant
of this matrix differs from zero, we determine the coefficients matrix
matrix and in this interval, where determinant
of this matrix differs from zero, we determine the coefficients matrix ![]() by formula (4).
by formula (4).
CONCLUSION
In this paper algorithm of the identification of systems parameters is worked out, when we have some restriction of system input and output variables and parameters. It means that model structure of system is known as a priori. The vector of input variables is continuous, and vector of output variables is continuous differentiable. It means, that variable coefficients are continuous. It is proved theorem about existence such interval, where this algorithm is right. In the paper is given example, where is illustrated the use of this algorithm for practical systems. Exactness of parameters estimations is depended on exactness of approximation input-output variables on the basis of data, which are received by observe of system's input- output. To protect from noise we recommend to use least squares method for the approximation input and output variables with continuous function.
REFERENCES
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|