 |
||
Tyatyushkin A.I.Russian, Irkutsk, Institute of System Dynamics and Control Theory of SB RAS
e-mail:snvas@icc.ru
MULTIMETHOD’S TECHNOLOGY IN OPTIMAL CONTROL PROBLEMS
Multimethod's technology for solving optimal control problems is implemented under the form of parallel optimization processes with the choice of a best approximation. Corresponding to this technology the solution is found by a multimethod’s algorithm consisting of a sequence of steps of different methods applied to the optimization process in order to accelerate it.
Тятюшкин А.И.
Россия, Иркутск, Институт динамики систем и теории управления СО РАН
e-mail:snvas@icc.ru
МНОГОМЕТОДНАЯ ТЕХНОЛОГИЯ В ЗАДАЧАХ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ
Многометодная технология решения задач оптимального управления реализуется в виде параллельных итерационных процессов оптимизации с выбором лучшего приближения. В соответствии с этой технологией решение задачи находится мультиметодным алгоритмом, состоящим из последовательности шагов разных методов, подключаемых к процессу оптимизации с целью его ускорения.
Technology of numerical solving of applied optimal control problems as usual is based on universal software which has well developed interface and rich arsenal of optimization methods. Such software allows to take into account a peculiarities of the problem under consideration by making of use diverse algorithmes of improvement at different stages of iteration process. Applcation of several numerical methods for solving single optimization problem was suggested in many works oriented on the development of software packages [2,3].
Principal difficulty in applying of multimethod's technology consists of the fact that at each stage in the process of solving of the problem, one has information about efficiency of the method applied at the present moment. To detect the efficiency of any optimization method at some stage of looking for a solution of the given problem, there is a need to perform one or several iterations. Because of this, to choose the method which is more appropriate for given stage of solving of the problem, the operation of switching from one method to another is usually repeated.
Let us consider optimal control problem provided by conditions in the
form of the equalities at the right trajectory end. Controlled process is described by the
system ![]() . (1)
. (1)
The control is constrained through
![]() (2)
(2)
where U is bounded closed set in Rr,
![]() . (3)
. (3)
The gradients of functionals![]() , in terms
of the functions
, in terms
of the functions ![]() and adjoint system
and adjoint system
![]() (4)
(4)
are given by the formula ![]()
Let us turn our attention to the discussion of the algorithms being
destinated for solving of the problems provided by constraints on control, but with free
right end. Suppose that for some ![]() one
finds any solution of the system (1)
one
finds any solution of the system (1) ![]() .
Setting in (5) j=0, integrate adjoint system from
.
Setting in (5) j=0, integrate adjoint system from ![]() to
to ![]() when
when ![]() . Calculate, on its solution
. Calculate, on its solution ![]() , the cotrol using the maximum principle:
, the cotrol using the maximum principle: ![]() and find the value of scalar function
and find the value of scalar function
![]()
Let ![]() the maximum point of this function
being on T. Then necessary optimum condition of the control
the maximum point of this function
being on T. Then necessary optimum condition of the control ![]() will be
will be ![]()
In the case when, for given ![]() and obtained
and obtained ![]() , maximum
principle
, maximum
principle ![]() is broken then one can realize
iteration of the method [1] to improve
is broken then one can realize
iteration of the method [1] to improve ![]() .
.
The point set, where maximum principle is broken, denote by
![]()
Observe, that at ![]() we have
we have ![]() , while at
, while at ![]() the set
the set ![]() consists of the
maximum points of the function
consists of the
maximum points of the function ![]() .
.
Varying ![]() , one can find such its value,
for which the control
, one can find such its value,
for which the control
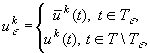 (5)
(5)
provides a least value of the purposeful functional ![]() , i.e.
, i.e. ![]()
When looking for ![]() , one
can use several flows for simultaneous integration of the system (1) with controls (5),
corresponding to different values of
, one
can use several flows for simultaneous integration of the system (1) with controls (5),
corresponding to different values of ![]() . In
addition, at
. In
addition, at ![]() we have different phase space
points
we have different phase space
points ![]() and pertinent values
and pertinent values ![]() . Choosing the smallest value of the functional
. Choosing the smallest value of the functional
![]() , verify the inequality
, verify the inequality ![]() . In the case if one holds, we set
. In the case if one holds, we set ![]() . Otherwise, one can continue the subdivision of
. Otherwise, one can continue the subdivision of
![]() and find the values of functional for the
following its values.
and find the values of functional for the
following its values.
By virtue of structure of the controls, generated by the iteration formula (5), the relaxationness of an algorithm can be impaired still before obtaining the control satisfying maximum principle. Because of this, to continue optimization process, there is a need to apply another algorithm, on iteration of which controls constructed not only with boundary points, but also with interior ones w.r.t. the set U as well. For example, to restore the covergence as usual succed with the help of construction using convex combination of two control
![]() (6)
(6)
The calculations by the formulas (5) and (6), one can perform
simultaneously choosing from obtained approximations such ![]() to which corresponds the smallest value of the functional. In the
case, if the values of the functional are compared within several iterations, then as
criterion to compare the efficiency of the methods (5) and (6), one should use the values
of an increase of the functional, obtained on neighboring iterations of each methods.
to which corresponds the smallest value of the functional. In the
case, if the values of the functional are compared within several iterations, then as
criterion to compare the efficiency of the methods (5) and (6), one should use the values
of an increase of the functional, obtained on neighboring iterations of each methods.
In actual practice, it is established that application of the variations of two type, namely, “horizontal” (5) and “vertical” (6), allows us to avoid an appearence of such effect like “stiking of control to the boundaries”, which is peculiar to the algorithms based on maximum principle [1, 3].
In the case, in iteration formula (6), one derives the control ![]() using linearized maximum principle
using linearized maximum principle
![]() (7)
(7)
iterations will be of conditional gradient method. It is evident, that
for systems which is linear in control, the control function (7) coincides with that
deduced from the maximum principle. A further algorithm of improving of control, one can
obtain substituting, in the iteration formula (5), the interval ![]() for the following one:
for the following one:
![]()
where ![]() are the nearest left and right
discontinuity points of the function
are the nearest left and right
discontinuity points of the function ![]()
In the process of finding of the value of the parameter ![]() , provided a convergence of the algorithm, one
can apply the procedure above with making of use parallel computations. This way to
construct the interval provides blowing down of its ends towards the point
, provided a convergence of the algorithm, one
can apply the procedure above with making of use parallel computations. This way to
construct the interval provides blowing down of its ends towards the point ![]() , in the case, if the function
, in the case, if the function ![]() is constant within some neighborhood of the
point
is constant within some neighborhood of the
point ![]() preserving by this a convergence of
the algorithm [1].
preserving by this a convergence of
the algorithm [1].
The block-scheme of multimethod's algorithm work. Summurizing above we see that applying various iteration procedures and making of use different rules to construct the sets of varying of control, we obtain the collection of algorithm, each of them works effectively enough only in a definite situation. Thus, in the process of finding of optimal control, it is necessary to include several algorithms.
Organizing parallel computations to realize some collection of algorithms and applying the selection procedure to take the best approximation after simultaneous iterations by all methods, we are able to find effectively optimal control by multimethod's algorithm.
Fig. 1. The scheme of realization of (k+1)-th iteration by multimethod’s algorithm
using three methods M1, M2, M3.
Fig. 1 informs us about work of multimethod's algorithm, in the case
when one uses three methods. In this, the block of selection of the best approximation
finds ![]() from a largest value of increment of
the functional obtained on (k+1)-th iteration
from a largest value of increment of
the functional obtained on (k+1)-th iteration ![]() This approximation is passed to all methods
This approximation is passed to all methods ![]() to perform next iteration.
to perform next iteration.
It should be noted that, that from the common methods collection, for solving another problem, it can be generated another multimethod's algorithm which would be more adequate, because of taking into account the peculiarities of this problem.
Using different criterions for choosing closest optimization method and also organizing in different ways parallel computations on the method's iterations, one can obtain several different combinations of algorithmes for solving a single problem. Moreover, it can be constructed such multimethod's algorithms which no contains repeated computations on the iterations of different optimization methods. For example, in the methods of gradient type, laborious computations of the gradient, requiring an integration of the adjoint system, should be performed only once, then, obtained gradient should be used in the iterative formulas of all methods. In this case, computational expanditures on one step of multiflow's algorithm are considerably reduced. Moreover, a realization of the step by any of the methods is accomplished by using the same approximately obtained values. Then all optimization algorithmes are applied as if to the one and the same approximate model. Thus the criterion of the new approximation is defined only by the optimization methods. Otherwise, because of computational errors, the same parameters used to estimate a convergence of the methods could have different values what can lead to improper choice of the best method.
Thus, we can coclude, that for each problem under consideration there exists appropriate sequence of steps using different methods which provides more effective search of optimal control. In multimethod's algorithmes the construction of such sequence is accomplished automatically using some given criterion estimating the efficiency of optimization process at each stage of solving of the problem. The base for application of the technology described above is the packages of applied software, for example, [2, 3, 4], which include the methods of first- and second-order, for solving optimal control problems with constraints of different types.
References:
[1] O.V. Vasil'ev, A.I. Tyatyushkin, On some method of solving of optimal control problems based on maximum principle, Journ. vychisl. matem. i mat. fiziki, Vol. 21, No. 6, 1981, pp. 1376-1384.
[2] Yu.G. Evtushenko, Methods of solving of extremal problems and its application, Nauka, Moscow, 1982.
[3] A.I. Tyatyushkin, Numerical methods and software for optimization of cotrolled systems, Nauka, Novosibirsk, 1992.[4] A.I. Tyatyushkin, A.I. Zholudev, N.M. Erinchek, The program system for solving optimal control problems with phase constraints, Intern. Journal of Software Engineering and Knowledge Engineering, Vol.3, No.4, 1993, pp.487-497.
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|