 |
||
Krasnoshtanov A.P., Kupriyanova E. V., Protsykova M. A., Rakovskaia S.A., Slonova L. A.
RUSSIA, Krasnoyarsk
THE IDENTIFICATION OF MULTIPLY CONNECTED SYSTEMS UNDER
INCOMPLETE INFORMATION
Annotation. The problems of interconnected stochastic systems identification in the broad sense are considered in this work. In addition the priory information about the parametric model structure is absent. Under these conditions the nonparametric modeling occurs to be perspective.
Красноштанов А., П.Куприянова Е. В., Процыкова М. А., Раковская С. А., Слонова Л. А.
Россия, Красноярск
ИДЕНТИФИКАЦИЯ МНОГОСВЯЗНЫХ СИСТЕМ ПРИ НЕПОЛНОЙ ИНФОРМАЦИИ
Аннотация. В докладе рассматриваются задачи идентификации взаимосвязанных стохастических систем в широком смысле. При этом априорная информация о параметрической структуре модели отсутствует. В этих условиях перспективным оказывается непараметрическое моделирование.
Пусть ![]() -векторы
наблюдаемых случайных последовательностей,
представляющие собой соответственно выходные и
входные переменные исследуемого процесса.
Определим функцию решений
-векторы
наблюдаемых случайных последовательностей,
представляющие собой соответственно выходные и
входные переменные исследуемого процесса.
Определим функцию решений ![]() как некоторую функцию, представляющую
собой выход (решение) адаптивной системы, a
функцию отклика
как некоторую функцию, представляющую
собой выход (решение) адаптивной системы, a
функцию отклика ![]() будем
рассматривать как реакцию исследуемого процесса
на. вход адаптивной системы. Пример разомкнутой
схемы представлен на рис.1.
будем
рассматривать как реакцию исследуемого процесса
на. вход адаптивной системы. Пример разомкнутой
схемы представлен на рис.1.
Рис. 1
В дальнейшем в наблюдаемых переменных
индекс ![]() из соображений
простоты опущен. Помехи
из соображений
простоты опущен. Помехи ![]() и
и
![]() таковы, что
таковы, что ![]() Сформируем критерий
оптимальности
Сформируем критерий
оптимальности
![]() (1)
(1)
где ![]() некоторая выпуклая функция. Задача отыскания
наилучшего
некоторая выпуклая функция. Задача отыскания
наилучшего ![]() сводится к
минимизации
сводится к
минимизации ![]() по
по ![]() , т. е. к поиску такого
, т. е. к поиску такого ![]() опт, что
опт, что ![]() Ясно, что вид
Ясно, что вид ![]() будет определяться видом
функции Q. Если
будет определяться видом
функции Q. Если ![]() , то
, то
![]() . (2)
. (2)
Можно рассмотреть и другие типы ![]() .
.
В дальнейшем вопрос состоит в
оценивании ![]() (u) по
наблюдениям
(u) по
наблюдениям ![]() , которые
формируются из исходных выборок
, которые
формируются из исходных выборок ![]() Знак ® означает
временной вектор.
Знак ® означает
временной вектор.
При пассивном накоплении информации,
т. е. при наличии выборки![]() непараметрический алгоритм оценивания (2) имеет
вид
непараметрический алгоритм оценивания (2) имеет
вид
![]() (3)
(3)
где матрицы ![]() таковы, что
таковы, что![]()
![]()
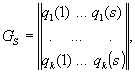
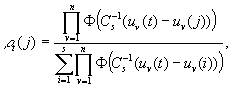
где T – знак транспонирования.
В случае, если закон имеет ярко
выраженный несимметричный характер, то можно
использовать вероятностные модели. В качестве
функции ![]() в критерии
оптимальности (1) выберем
в критерии
оптимальности (1) выберем ![]() где
где ![]() -
дельта-функция Дирака. При минимизации этого
критерия по
-
дельта-функция Дирака. При минимизации этого
критерия по ![]() получаем
моду условной плотности распределения
получаем
моду условной плотности распределения ![]() Тогда
Тогда
![]() (4)
(4)
Важным с практической точки зрения является исследование регрессионных моделей в нестационарных условиях. Предполагается, что вероятностные характеристики объекта меняются во времени неизвестным образом. Непараметрическая оценка функции регресии имеет вид:
fs(x)=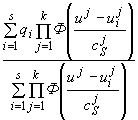 , (5)
, (5)
которую следует модифицировать, вводя в неё дополнительные веса – некоторые “функции памяти”, убывающие с ростом [s-i]. Этот факт соответствует “забыванию” старой информации.
Существенный интерес, с точки зрения
практики, представляет собой случай, когда для
некоторых зависимостей компонент векторов ![]() и
и ![]() известна их параметрическая зависимость
с точностью до
известна их параметрическая зависимость
с точностью до![]() набора
параметров
набора
параметров ![]() . В этой
ситуации мы сталкиваемся с задачей
идентификации, которая не соответствует ни
параметрическому уровню априорной информации,
ни непараметрическому. Такие модели возникают
при описании сложных взаимосвязанных процессов
(часто эта ситуация возникает при моделировании
производственных процессов с непрерывной
технологией) и имеют вид взаимосвязанной системы
. В этой
ситуации мы сталкиваемся с задачей
идентификации, которая не соответствует ни
параметрическому уровню априорной информации,
ни непараметрическому. Такие модели возникают
при описании сложных взаимосвязанных процессов
(часто эта ситуация возникает при моделировании
производственных процессов с непрерывной
технологией) и имеют вид взаимосвязанной системы
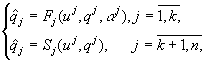 (6)
(6)
где индекс ![]() при аргументах
при аргументах ![]() означает
определенный (
означает
определенный (![]() й) набор
этих компонент из всех компонент,
й) набор
этих компонент из всех компонент, ![]() ая параметрическая модель,
ая параметрическая модель, ![]() непараметрическая (
непараметрическая (![]() ая) модель,
ая) модель, ![]() вектор выходных переменных модели,
вектор выходных переменных модели, ![]() входных,
входных, ![]() оценка параметров.
оценка параметров.
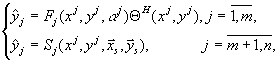 (7)
(7)
где ![]() выборка
статистически независимых наблюдений (
выборка
статистически независимых наблюдений (![]() ) объема
) объема ![]() . При использовании H-моделей (7)
исключаются те дефекты, которые возможны при
применении моделей (6). Ясно, что, если
. При использовании H-моделей (7)
исключаются те дефекты, которые возможны при
применении моделей (6). Ясно, что, если ![]() то модели (7) переходят в
модели (6).
то модели (7) переходят в
модели (6).
Пусть производственный комплекс представляет собой некоторый агрегат взаимосвязанных технологических аппаратов (объектов), модели которых обозначим
![]() где
где ![]() соответственно выходная и
входная переменные 1-го объекта,
соответственно выходная и
входная переменные 1-го объекта, ![]() параметрическая зависимость
параметрическая зависимость ![]() от
от ![]() с точностью до параметров
с точностью до параметров ![]() а
а ![]() число
объектов. В случае, если все модели построены
(некоторые из них могут быть моделями
непараметрического типа), то часто возникает
задача построения модели всего комплекса.
Естественно для этой цели использовать модели
локальных объектов
число
объектов. В случае, если все модели построены
(некоторые из них могут быть моделями
непараметрического типа), то часто возникает
задача построения модели всего комплекса.
Естественно для этой цели использовать модели
локальных объектов ![]() Но
арифметическая “сборка” этих моделей, как
правило, не обеспечивает необходимой точности. В
технике аналогом подобного факта является
сборка некоторого изделия из отдельных блоков,
каждая из которых удовлетворяет техническим
условиям, но функционирование всего изделия не
отвечает соответствующим техническим
требованиям и поэтому возникает необходимость
настройки всего изделия, которая представляет
собой одновременную настройку всех или
некоторых локальных блоков. Процесс “сборки”
макромодели из локальных и их последующую
“настройку” мы назвали макросинтезом моделей.
Но
арифметическая “сборка” этих моделей, как
правило, не обеспечивает необходимой точности. В
технике аналогом подобного факта является
сборка некоторого изделия из отдельных блоков,
каждая из которых удовлетворяет техническим
условиям, но функционирование всего изделия не
отвечает соответствующим техническим
требованиям и поэтому возникает необходимость
настройки всего изделия, которая представляет
собой одновременную настройку всех или
некоторых локальных блоков. Процесс “сборки”
макромодели из локальных и их последующую
“настройку” мы назвали макросинтезом моделей.
ЛИТЕРАТУРА
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|