В докладе рассмотрены регрессионные модели, которые хотя и являются нелинейными функциями во всей допустимой области изменения входных переменных, но возможна аппроксимация их линейными функциями в пределах отдельных подобластей пространства входов.

На каждой из подобластей изменения входных переменных основной особенностью является наличие автокоррелированного шума в канале наблюдений, причем модель задается в форме линейного разностного уравнения.

Описание динамических объектов линейными разностными уравнениями зависит от точки приложения помехи. При наличии помехи на входе прямого канала (перед оператором канала обратной связи) использование обычной процедуры метода наименьших квадратов (МНК) позволяет получать сильно состоятельные оценки при довольно слабых ограничениях на входной сигнал и помеху. Но в случае приложения аддитивной помехи в выходном канале объекта задача идентификации становится уже задачей регрессионного анализа с ошибками в независимых переменных; при этом оценки параметров, полученные с использованием обычного МНК, будут несостоятельными, даже если помеха – стационарный дискретный белый шум.

В докладе описывается алгоритм нелинейного МНК для идентификации параметров линейных разностных уравнений при аддитивном локально автокоррелированном шуме в канале наблюдения. Доказывается сильная состоятельность предлагаемых оценок при условиях на входной сигнал и помеху. Рассматриваются вопросы существования этих оценок. Доказательство сильной состоятельности основано на теореме сходимости мартингала и лемме Кронекера.

Рассмотрим стационарную динамическую систему, описываемую следующим линейным разностным уравнением заданного порядка с дискретным временем

(1)

и выходная переменная наблюдается с аддитивным шумом в виде

(2)

где - оператор запаздывания;

и - наблюдаемые входной и выходной сигналы соответственно;

- ненаблюдаемый выходной сигнал;

- ненаблюдаемый шум;

- неизвестные вещественные истинные значения параметров.

Требуется по наблюдаемым конечным реализациям и определить оценки неизвестных истинных значений параметров при следующих предположениях:

1). Случайный процесс удовлетворяет условиям:

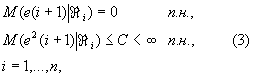
где - условное математическое ожидание;

алгебра, индуцированная семейством случайных величин множество целых чисел

2). Выполняются следующие условия:

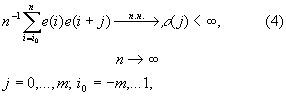
где локальная автоковариационная функция.

матрица

положительно определенная, где Т- знак транспонирования, а матрица К:

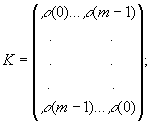
вектор .

3). Случайные величины не зависят от

4). Истинные значения параметров удовлетворяют условиям стационарности, т.е. корни характеристического уравнения

лежат вне единичного круга.

5). Входной сигнал является случайным процессом и удовлетворяет условиям постоянного возбуждения порядка q, т.е. с вероятностью 1 существует

и матрица положительно определенная, где - множество прямоугольных вещественных матриц размерности (q+1)· (q+1);

Пусть стационарная динамическая система описывается уравнениями (1), (2) и помеха удовлетворяет предположениям (3)-(5).

Тогда при с вероятностью 1 существует оценка

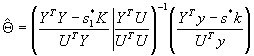
где - наименьший корень уравнения,

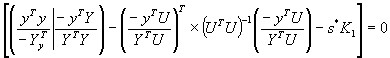
а

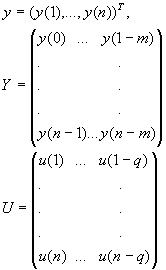
при этом оценка - сильно состоятельная.

В докладе приведены программное обеспечение и тесты.