Ethan Frome

Tyatyushkin A.I.

Russia, Irkutsk, Institute of System Dynamics & Control Theory of SB RAS

e-mail: rozen@icc.ru

MULTIMETHOD'S TECHNOLOGY IN OPTIMAL CONTROL PROBLEMS

Multimethod's technology for solving optimal control problems is implemented under the form of parallel optimization processes with the choice of a best approximation. Corresponding to this technology the solution is found by a multimethod's algorithm consisting of a sequence of steps of different methods applied to the optimization process in order to accelerate it.

Тятюшкин А. И.

Россия, Иркутск, Институт динамики систем и теории управления СО РАН

e-mail:rozen@icc.ru

МНОГОМЕТОДНАЯ ТЕХНОЛОГИЯ В ЗАДАЧАХ ОПТИМАЛЬНОГО УПРАВЛЕНИЯ

Многометодная технология решения задач оптимального управления реализуется в виде параллельных итерационных процессов оптимизации с выбором лучшего приближения. В соответствии с этой технологией решение задачи находится мультиметодным алгоритмом, состоящим из последовательности шагов разных методов, подключаемых к процессу оптимизации с целью его ускорения.

Решение сложной задачи оптимизации не всегда удается получить с помощью одного численного метода, поэтому существующие программные системы оптимизации [2,3] обычно предусматривают возможность применения многометодной технологии в диалоговом режиме. В случае прекращения сходимости итерационного процесса пользователь подбирает другой метод и, если выбор окажется неудачным, то осуществляется переход к следующему методу. Недостатком такой технологии является необходимость "ручного" выбора наиболее соответствующего для данной стадии решения задачи метода оптимизации.

В докладе предлагается новый подход для реализации многометодной технологии решения задач оптимального управления:

, (1)

( где U ограниченное замкнутое множество в R^r), (2)

min (3)

Градиент функционала I(U) с помощью функции и сопряженной системы

(4)

определяется по формуле

Алгоритмы, основанные на принципе максимума. На основе применения параллельных процессов для поиска приближенного решения задачи будем одновременно использовать несколько итерационных методов первого порядка.

Предположим, что при некотором найдено решение системы (1) . Проинтегрируем сопряженную систему от t=t₁ до t= t₀ при . На ее решении вычислим управление из принципа максимума:

и найдем значения скалярной функции

Пусть - точка максимума этой функции на Т. Тогда необходимым условием оптимальности управления и^k будет равенство

Если для заданного u^k и найденных ' принцип максимума нарушается:

то можно реализовать итерацию метода [1] для улучшения u^k.

Множество точек, в которых нарушается принцип максимума, обозначим через

Заметим, что при = 0 будем иметь , а при = 1 множество Т будет состоять из точек максимума функции .

Варьируя , можно найти его оптимальное значение, при котором управление

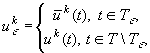(5)

доставит наименьшее значение целевому функционалу I{и):

При поиске можно использовать несколько потоков для одновременного интегрирования системы (1) с управлениями (5), соответствующими разным значениям .При t = t₁ будем иметь при этом разные точки фазового пространства и соответствующие им значения. Выбрав наименьшее значение функционала, проверим неравенство и, если оно выполняется, то полагаем . В противном случае можно продолжить дробление и найти значения функционала для следующих его значений.

В силу структуры управлений, генерируемых итерационной формулой (5), релаксационность алгоритма может ухудшиться еще до получения управления, удовлетворяющего принципу максимума. Поэтому для продолжения процесса оптимизации необходимо применить другой алгоритм, на итерациях которого строятся управления не только с граничными, но и с внутренними относительно множества U значениями. Так, например, восстановить сходимость обычно удается с помощью построения выпуклой комбинации двух управлений:

(6)

Вычисления по формулам (5),(6) можно вести параллельно, выбирая из полученных приближений такое которому соответствует меньшее значение функционала. Если значения функционала будут сравниваться через несколько итераций, то в качестве критерия для сравнения эффективности методов (5) и (6) следует использовать значения приращений функционала, полученные на соседних итерациях каждого из методов.

На практике установлено, что применение вариаций двух типов: "горизонтальной" (5) и "вертикальной" (6) позволяет избежать проявления эффекта "прилипания управления к границам", свойственного алгоритмам, основанным на принципе максимума [1,2].
Если в итерационной формуле (6) управление будет вычисляться из линеаризованного принципа максимума:

(7)

то получим итерации метода условного градиента. Очевидно, для систем, линейных по управлению, управление (7) будет совпадать с управлением, найденным из принципа максимума.

Еще один алгоритм улучшения управления можно получить, заменив в итерационной формуле (5) отрезок на следующий:

(8)

где - ближайшие слева и справа точки разрыва функции

При этом для поиска значения параметра , обеспечивающего сходимость алгоритма, можно применить описанную выше процедуру с использованием параллельных вычислений. Такое правило построения отрезка обеспечивает стягивание его концов к точке и в том случае, когда функция постоянна в некоторой окрестности точки , сохраняя тем самым сходимость алгоритма [I].

Схема функционирования мультиметодного алгоритма. Таким образом, применяя различные итерационные процедуры и используя разные правила для построения множества варьирования управления, мы получили группу алгоритмов, каждый из которых работает достаточно эффективно только в определенной ситуации. Следовательно, в процесс поиска оптимального управления целесообразно включить все эти алгоритмы.

После выполнения нескольких итераций среди полученных разными методами приближений следует выбрать наилучшее, например, по наибольшему приращению функционала. Начиная с этого приближения, далее стартуют все методы и вновь выполняют несколько итераций, после чего лучшее из полученных приближений опять передается всем методам для продолжения итерационного процесса. В результате к поиску решения задачи будет применен алгоритм, состоящий из последовательности шагов разных методов, который будем называть мультиметодным алгоритмом.

На рис.1 показана схема работы мультиметодного алгоритма для случая, когда группа состоит из трех методов. Блок выбора лучшего приближения находит по наибольшему значению приращения функционала, полученного на (k + 1)-ой итерации:

Затем это приближение передается всем методам: для выполнения следующей итерации.

Заметим, что из одной и той же группы методов оптимизации при решении другой задачи может сгенерироваться совсем другой мультиметодный алгоритм, который будет более адекватно учитывать особенности новой задачи.

Таким образом, в процессе параллельного применения нескольких методов среди них будет выбираться наиболее эффективный для каждой стадии решения задачи оптимального управления.

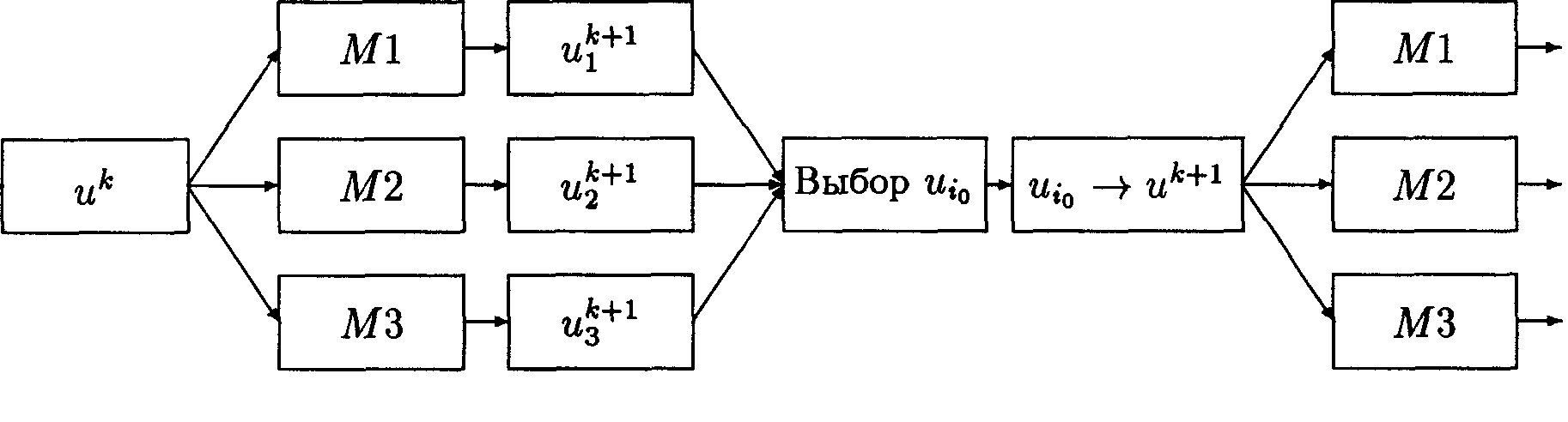
Рис. 1. Схема выполнения k + 1 - й итерации мультиметодным алгоритмом для группы из трех методов: Ml, M2, МЗ.

В результате приближённое решение задачи будет найдено мультиметодным алгоритмом, состоящим из последовательности шагов разных методов, подключаемых к процессу оптимизации, например, с целью наискорейшего убывания функционала. В сравнении с каждым из алгоритмов в отдельности мультиметодный алгоритм будет более адекватно учитывать особенности решаемой задачи, например, овражность целевой функций или структуру ограничений на переменные, используя на каждом этапе поиска решения наиболее эффективно работающий метод. Заметим также, что сходимость мультиметодного алгоритма будет сохраняться до тех пор, пока будет сходится хотя бы один из параллельно используемых методов.

Таким образом, можно сделать вывод, что для каждой задачи существует своя последовательность шагов из разных методов, которая обеспечивает наиболее эффективный поиск оптимального управления. В мультиметодных алгоритмах построение такой последовательности выполняется автоматически по некоторому заданному критерию, оценивающему эффективность процесса оптимизации на всех этапах решения задачи. Базой для применения описанной технологии являются пакеты прикладных программ, например, [2], которые включают методы первого и второго порядков для решения задач оптимального управления с ограничениями разного типа.

Литература

[1] Васильев О.В., Тятюшкин А.И. Об одном методе решения задач оптимального управления, основанном на принципе максимума // Журн. вычисл. матем. и мат. физики. - 1981. - Т. 21, No. 6. -С. 1376-1384.

[2] Тятюшкин А.И. Численные методы и программные средства оптимизации управляемых систем.— Новосибирск: Наука, 1992.

[3] Tjatjushkin A.I., Zholudev A.I., Erinchec N.M. The program system for solving optimal control problems with phase constraints // Intern. J. of Software Engineering and Knowledge Engineering. - 1993. Vol.3, No.4.- P. 487-497.

Site of Information Technologies
Designed by inftech@webservis.ru.