 |
||
Burakov M. V., Konovalov A.S.
Russia, St.-Petersburg, State university of aerospace instrumentation (GUAP) E-mail: BMV@ acts.aanet.ru
DESIGN OF INTELLECTUAL CONTROL SYSTEMS BY DYNAMIC OBJECTS BY A METHOD OF KNOWLEDGE BASE DECOMPOSITION.
The technique of designing of knowledge bases of intellectual control systems of complex objects is considered. It is offered to synthesize a knowledge base as a collection of cooperating subsystems deciding the local tasks of control. The variants of use of the offered approach are reduced with designing fuzzy and neuro controllers.
Бураков M. В., Коновалов А.С.
Россия, Санкт-Петербург, Государственный университет аэрокосмического приборостроения
(ГУАП), E-mail: BMV@acts.aanet.ru
РАЗРАБОТКА ИНТЕЛЛЕКТУАЛЬНЫХ СИСТЕМ УПРАВЛЕНИЯ ДИНАМИЧЕСКИМИ ОБЪЕКТАМИ МЕТОДОМ ДЕКОМПОЗИЦИИ БАЗЫ ЗНАНИЙ
Рассматривается методика конструирования баз знаний интеллектуальных систем управления сложными объектами. Предлагается синтезировать базу знаний как совокупность взаимодействующих подсистем, решающих локальные задачи управления. Приводятся варианты использования предлагаемого подхода при конструировании нечетких и нейронных регуляторов.
1. ПОСТАНОВКА ЗАДАЧИ
Родовым признаком любой системы искусственного интеллекта является наличие базы знаний (БЗ). Для нечетких регуляторов БЗ представлена в виде набора нечетких продукционных правил, а для нейронных регуляторов БЗ получает неявное представление в виде набора весов нейронной сети (НС) определенной топологии. Сложность задачи синтеза управляющей БЗ зависит от сложности объекта управления. Качество работы интеллектуального регулятора (ИР) со сложной БЗ трудно анализировать. Например, большое количество нечетких правил может вызывать “паралич” сигнала управления, а НС может обнаруживать заранее непрогнозируемые свойства. Поэтому в общем случае выгодно осуществлять декомпозицию сложной БЗ на относительно простые составляющие, а затем преобразовывать их сигналы в общий сигнал управления.
Рассмотрим традиционную постановку задачи управления. Пусть состояние динамической системы в каждый дискретный момент времени t описывается зависимостями:
Xt+1 =F(Xt, Ut), t=1,2…
Где Х — вектор состояния размерностью n, a U — вектор управления размерностью т. Вектор состояния определяет фазовое пространство (ФП), в котором происходит движение объекта. Решение задачи управления понимается как перевод объекта из некоторого начального состояния в некоторое заданное состояние.
При использовании линеаризованных моделей объектов регулятор работоспособен в некоторой окрестности заданной рабочей точки. Например, ПИД- регулятору для одномерной системы можно поставить в соответствие нейрон с тремя входами и линейной активационной функцией. Такая структура может решать только простые задачи управления.
ИР (нейронный регулятор, использующий множество нейронов, или нечеткий регулятор со множеством правил управления) реализует нелинейный закон управления, расширяющий диапазон работоспособности [1-3]. Однако при попытке описать закон управления для всего ФП объекта возникает ряд принципиальных трудностей.
Во-первых, задача синтеза регулятора характеризуется значительной неопределенностью. Построение продукционных правил при синтезе нечетких регуляторов при больших n может вызывать проблемы, так как резко растет число возможных правил управления и заранее невозможно оценить их достаточное количество. Точно также трудно оценить минимальную структуру НС, при которой возможно решение постав- ленной задачи с помощью нейронного регулятора.
Во-вторых, реальные системы характеризуются многомерностью. При обучении ИР нужно иметь не только модель объекта, но и физически реализуемый эталонный процесс. Но даже в этом случае нельзя гарантировать успешное обучение ИР с большим количеством входов и выходов. Например, при использовании для обучения генетического алгоритма резко растет длина хромосомы, и, соответственно, размер пространства поиска [4].
Поэтому выгодно рассматривать задачу управления объектом как совокупность задач, определенных для отдельных подпространств или отдельных точек ФП. Здесь можно выделить две постановки задачи:
1) Рассматривается управление в разных подпространствах ФП по-отдельности (этому соответствует независимая разработка отдельных контуров управления многосвязной системы), после чего сигналы управления согласуются для выработки общего сигнала управления;
2) Рассматривается движение по заданной траектории ФП, как последовательность перемещений из одной области ФП в другую. Каждой области соответствует локальный регулятор. На границах областей действия регуляторов согласовываются.
2. ДЕКОМПОЗИЦИЯ ЗАКОНА УПРАВЛЕНИЯ ДЛЯ МНОГОСВЯЗНОГО ОБЪЕКТА
Основная идея, заложенная в структуру рассматриваемого варианта построения ИР для многосвязного объекта, заключается в независимом формировании законов управлении разными выходными переменными объекта. Используется несколько контуров управления, реализующих собственные законы управления, их сигналы (в общем случае противоречивые) согласуются с помощью НС. Потенциальные преимущества такого подхода заключаются в следующем:
- правила управления в отдельных контурах могут быть достаточно очевидны или получены после простой процедуры обучения;
- отдельные контуры управления могут иметь много входов (переменные состояния объекта) и мало выходов (сигналы управления), что позволяет использовать сравнительно простую согласующую НС.
Рассмотрим в качестве примера систему с двумя равноправными контурами управления (рис.1), где через Xi(t) обозначены вектора, составленные из отдельных компонент вектора состояния X(t).
Если Б31 и Б32 представляют собой набор нечетких продукционных правил, то основное преимущество здесь заключается в уменьшении числа посылок правила, т.к. рассматривается не полный, а усеченный вектор состояния. Если Б31 и Б32 построены на основе НС, то она в этом случае может иметь более простую структуру из-за уменьшения числа входов. В обоих случаях проще решается задача обучения, поскольку уменьшается сложность минимизируемой функции ошибки.
Б31 и Б32 должны быть построены до того, как настраивается БЗЗ, представляющая собой нейронную сеть прямого распространения. Она решает уже полную задачу управления, но получает на вход не многокомпонентный вектор X, а всего 4 переменные (для рис. 1).
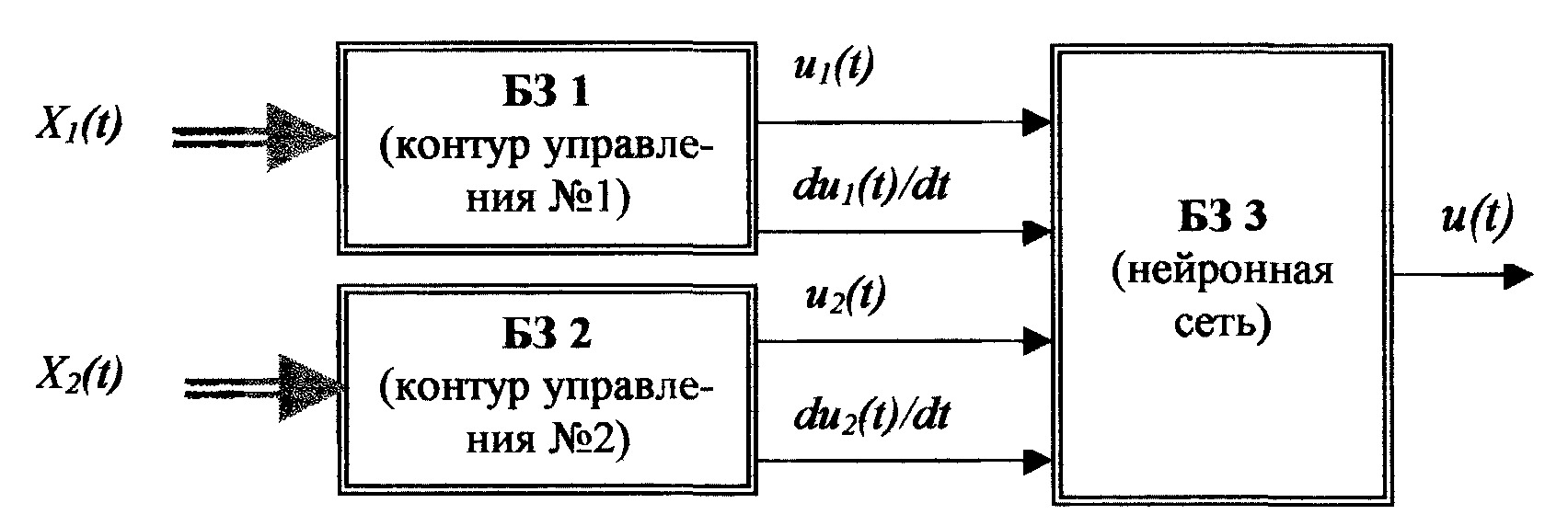
Рис. 1. Пример декомпозиции БЗ для многосвязного объекта.
Успех решения задачи при таком подходе зависит от того, может ли рассматриваться набор {ui , dui /dt} в качестве описания ситуации на объекте, эквивалентного описанию с помощью набора координат: {хi}.
Для проверки возможности предлагаемой
методики была рассмотрена классическая задача
управления перевернутым маятником (см., например,
[4]). Объект управления имеет две выходные
переменные: расстояние от исходной точки S и
угол отклонения маятника ![]() от вертикали. Задача управления
заключается в стабилизации маятника в положении S=0
и
от вертикали. Задача управления
заключается в стабилизации маятника в положении S=0
и ![]() =0. Для каждой из
координат формируется таблица лингвистических
правил (ТЛП), реализующая нечеткий закон
управления. В итоге получаются два нечетких
регулятора, независимо управляющих каждой из
переменных. Как показало моделирование,
согласование сигналов от двух ТЛП с помощью
простой НС возможно после несложной процедуры
обучения с использованием генетического
алгоритма.
=0. Для каждой из
координат формируется таблица лингвистических
правил (ТЛП), реализующая нечеткий закон
управления. В итоге получаются два нечетких
регулятора, независимо управляющих каждой из
переменных. Как показало моделирование,
согласование сигналов от двух ТЛП с помощью
простой НС возможно после несложной процедуры
обучения с использованием генетического
алгоритма.
3. ДЕКОМПОЗИЦИЯ УПРАВЛЕНИЯ ПРОГРАММНЫМ ДВИЖЕНИЕМ
Задача управления объектом может существенно меняться при переходе из одной точки ФП в другую. Рассмотрим эту проблему на конкретном примере - задаче управления посадкой самолета вертикального взлета и посадки (СВВП). Программа посадки СВВП включает три этапа [5]:
1) Снижение до заданной малой высоты;
2) Горизонтальный полет с гашением скорости до малой величины;
3) Посадка в точку со скоростями, близкими к нулевым.
Для решения этой задачи может быть использован нейронный регулятор. Однако, как показали опыты, НС в этом случае должна быть многослойной, процедура обучения оказывается труднореализуемой, а точность решения задачи не может быть гарантирована. Это является следствием известной проблемы стабильности - пластичности НС [б], что в данном случае означает "забывание" одного маневра при обучении другому маневру.
Поэтому в данном случае оказывается выгодным проводить декомпозицию закона управления и самой НС в соответствии с рис.2.
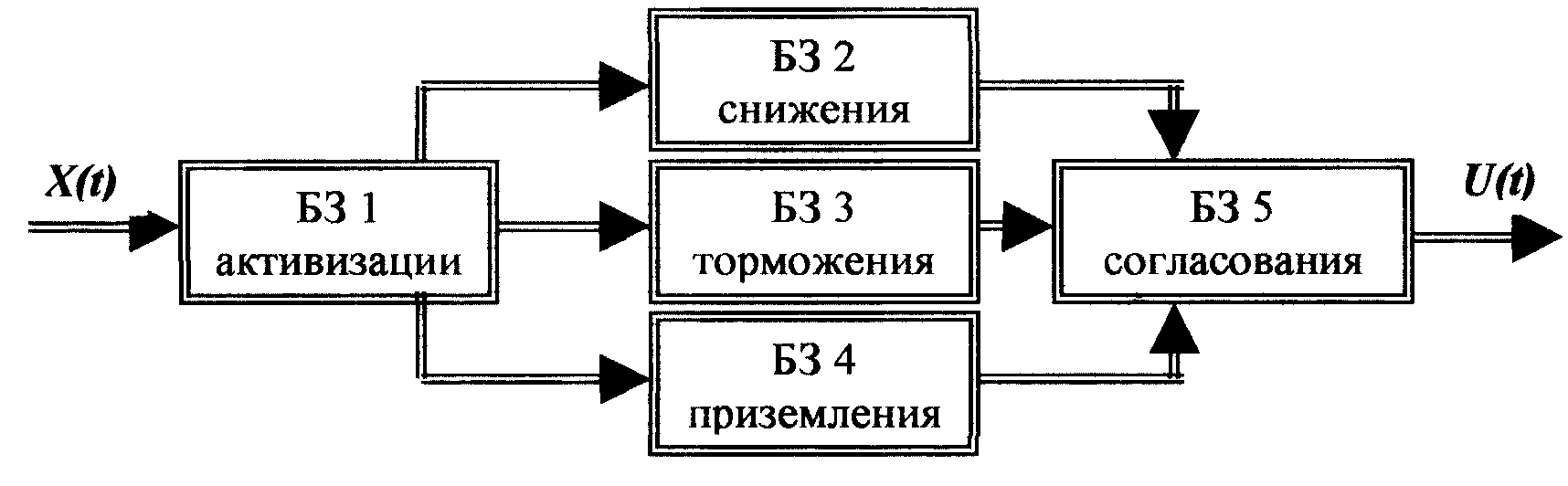
Рис. 2. Пример декомпозиции БЗ при посадке СВВП.
Б31 оценивает текущее состояние объекта и активизирует один или больше законов управления, хранящихся в Б32, БЗЗ и Б34. Б35 должна сглаживать противоречия в тех случаях, когда одновременно активны две или три БЗ управления.
Содержимое Б31 достаточно очевидно, это может быть набор продукционных правил, описывающих условия срабатывания управляющих БЗ. Б32 - Б34 представляют собой НС прямого распространения. Как показало моделирование, в рассматриваемой задаче вполне удовлетворительными оказываются однослойные НС, а процедура обучения достаточно проста. Задача обучения Б35 практически аналогична задаче обучения БЗЗ (рис.1).
4. ЗАКЛЮЧЕНИЕ
Предложенные подходы позволяют контролировать процесс синтеза ИР с тем, чтобы сложность обучения отдельных подсистем управления не превышала некоторого порога, за которым возникают непреодолимые трудности. При этом закон управления может постепенно совершенствоваться путем описания новых контуров или добавления новых режимов движения, реализованных в виде отдельных БЗ.
ЛИТЕРАТУРА
1. Бураков М.В., Попов О.С. Элементы искусственного интеллекта в проблеме управления сложным динамическим объектом // Автоматика и телемеханика, № 8, 1997г. С. 118-124.
2. Бураков М.В. Механизм адаптации нечеткого регулятора. // Известия Академии наук. Теория и системы управления. 1998, №1, С.84-87.
3. Бураков М.В., Коновалов А.С., Попов О.С. Адаптивное управление сложными объектами // Оборонная техника, №6-7, 1998г. с. 56-61.
4. Бураков М.В. Синтез нейронного регулятора // Изв. Академии наук. Теория и системы управления, 1999, №3, С.140-145.
5. Батенко А.П. Системы терминального управления. - М.:Радио и связь, 1984. - 160с.
6. Warwick К., Irwin G.W., Hunt K.J. Neural Networks for Control. Cambridge, MA:
MIT Press, 1990.
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|