(St.-Petersburg) Russia

Institute of Problems of Mechanical Engineering

E-mail: gae@msa.ipme.ru

In the state-space (SS) of nonlinear non-stationary dynamic objects (DO) are investigated numerical algorithms of their optimum control with restrictions on phase coordinates. The dynamic process is interpreted as growth of the binary trees (ВТ). In accordance with growth ВТ, it the knots get into various areas of the SS (clusters). . The purpose of control is the get, during growth ВТ, a knot in a specific cluster (target set) for the minimum number of steps.

(Санкт-Петербург) Россия

Институт Проблем Машиноведения РАН

E-mail: gae@msa.ipme.ru

Исследуются численные алгоритмы оптимального управления нелинейных нестационарных динамических объектов (ДО) при наличии ограничений. В пространстве состояний (ПС) динамический процесс интерпретируется как рост бинарного дерева (БД). По мере роста БД, его узлы попадают в различные области ПС (кластеры). Целью управления является попадание, в процессе роста БД одного из узлов в заданный кластер за минимальное число шагов.

В настоящем докладе дается изложение и интерпретация алгоритмов "Метода поиска оптимальных управляющих воздействий на динамические объекты с адаптацией к изменениям внешней среды" [ 1] . Управляющие воздействия ограничиваются классом кусочно-постоянных функций, в виде положительных и отрицательных импульсов, порождающих в ПС бинарные деревья (БД). Ограничения, накладываемые на фазовые координаты ДО, образуют границы запретных областей для узлов БД. В узлах, попавших на границы запретных областей, эволюция БД заканчивается. С течением времени в одни и те же кластеры могут попадать новые узлы дерева и образовывать циклы. Для исключения зацикливаний, в этих узлах эволюция БД также завершается.

Целью управления является отыскание допустимой управляющей функции, переводящей ДО из начального состояния в некоторую точку целевого множества за минимальное число шагов и удержание ДО в этом целевом множестве, путем периодического прогнозирования решения на заданном интервале времени прогнозирования. Оптимальная фазовая траектория при этом должна удовлетворять ограничениям. В теории оптимального управления такую задачу относят к вариационным задачам на максимальное быстродействие с подвижным правым концом и ограничениями типа неравенств [2].

Реализация алгоритмов регуляторов, основанных на этих методах, предназначенных для работы в реальном времени, представляет значительную трудность из-за сложности вычислительного процесса.

Поэтому для уменьшения сложности вычислений, оптимизационная “процедура отыскания управляющего воздействия осуществляется поэтапно, образно говоря, сначала на грубой сетке, с последующим уменьшением размеров ячеек этой сетки. Для этого область ПС ограничивается допустимыми интервалами для каждой компоненты ВС. Затем каждый допустимый интервал разбивается на заданное число подинтервалов. Произвольное сочетание подинтервалов, по одному на каждую компоненту ВС, интерпретируется как ограниченная область ПС и называется кластером. Вводится ограничение, согласно которому каждому кластеру может принадлежать только один узел БД.

Строится прогнозирующая модель, с помощью которой в каждом узле БД вычисляются оценка ВС ДО, запоминается и хранится в памяти ЭВМ в течении всего цикла прогнозирования. Управляющее воздействие определяется комбинаторным методом как логическая функция упорядоченного множества узлов БД.

ДО описывается системой обыкновенных дифференциальных уравнений в разностной форме

(1)

где: — функции времени t, , ; — такт

— ВС; , — матрицы параметров ДО;

—функция управления;

— функция возмущения ВС

Ограничения:

, (2)

(3)

— является кусочно-постоянной функцией на интервале и принимает одно из двух возможных значений .

Требуется найти кусочно-постоянную функцию , которая обеспечивает переход ДО из в за минимальное время или минимальное число шагов п.

При решении задач управления ДО при явно заданной целевой функции квадратичного критерия качества, отыскание управляющей функции не является принципиально проблематичной и связано с вычислительными трудностями технического характера [3]. Например, решение задачи синтеза системы управления с линейной обратной связью, оптимальной относительно некоторого квадратичного функционала, определяется исключительно возможностью численного решения матричного уравнения Риккати. Вопросы устойчивости вычислений при использовании того или иного метода решения уравнения Риккати определяются свойствами матриц ОУ, выбором начального приближения, а также особенностями применяемого вычислительного алгоритма и исследуются в каждом конкретном случае самостоятельно. Можно указать на два существенных недостатка синтеза систем управления с квадратичным критерием качества.

Первый недостаток определяется тем, что оптимальное решение справедливо только для стационарной точки. Другим существенным недостатком является проблема выбора весовых коэффициентов в квадратичном критерии качества.

Поэтому современные методы управления нестационарными ДО с ограничениями на ВС основываются на иных методах, вычислительной основой которых является математическое программирование [4].

Применение математического программирования для задач управления нелинейных ДО привело к большому числу различных алгоритмов, основными чертами которых являются поисковые переборные процедуры возможных решений. Практическое применение таких алгоритмов сдерживается из-за их большой вычислительной трудоемкости (сложности). Теоретическое обоснование принципиальной возможности уменьшения вычислительной сложности представляет самостоятельную проблему, которой посвящено значительное число работ [5]. По существу оценка вычислительной сложности любой задачи требующей численного решения является необходимой, так как определяет эффективность этого решения. Общепринятая методика исследования таких задач предполагает разложение или сведение исходной задачи к некоторому числу задач, для которых вычислительная сложность является известной. Обычно оценка сложности связывается с размерностью объектов, входящих в задачу. При этом возможны следующие пути решения:

- решение в один этап на мелкой сетке,

- последовательность решений в несколько этапов на крупной сетке. Решение в один этап на мелкой сетке связано с большой размерностью задачи, но с малой комбинаторной сложностью.

Последовательность решений в несколько этапов на крупной сетке на каждом этапе связана с малой размерностью задачи, но со сравнительно большой комбинаторной сложностью. Очевидно, возможен компромисс при выборе числа этапов и размеров ячеек сетки. Для переборных задач такой подход к решению в несколько этапов делает вычислительную сложность объектом оптимизации, что в конечном итоге может увеличить эффективность решения.

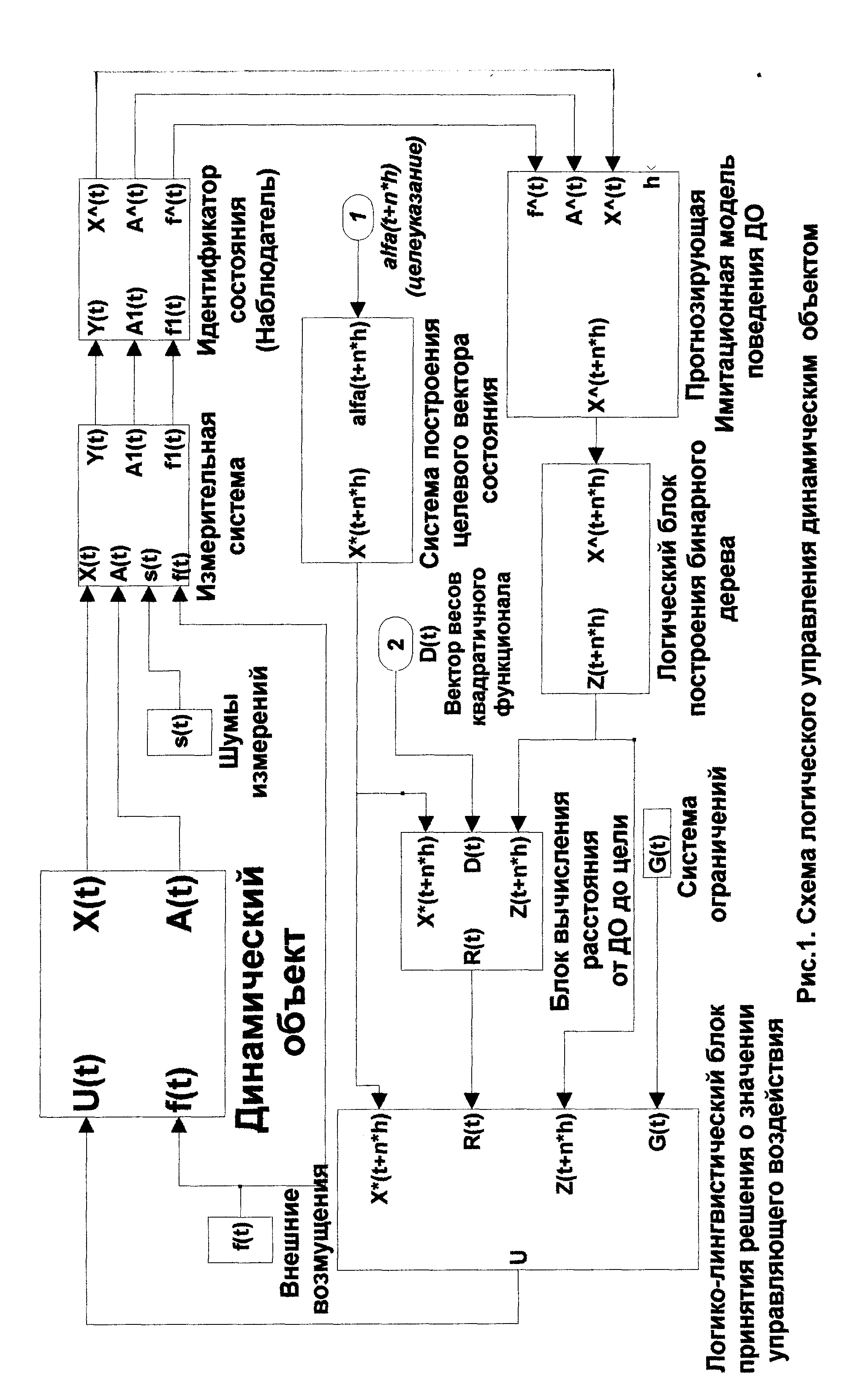
Логическое управление ДО в кластерном пространстве состояний является характерным примером указанного подхода. Структурная схема системы логического управления приведена на рис. 1.

Предлагается следующая стратегия управления:

1. Посредством прогнозирующей модели (ПМ) ДО вычисляются два ВС при заданном значении времени прогнозирования для двух постоянных, противоположных по значению управляющих воздействий ВС⁺ и ВС^-.
2. ВС нормируются путем деления их компонент на соответствующие максимально допустимые значения.
3. В нормированном пространстве определяются расстояния между целевой

точкой BC_g, точками ВС⁺ и ВС^-.

4. Выбирается тот знак управляющего воздействия, которому соответствует меньшее расстояние до целевой точки. Это управляющее воздействие подается на ДО.
5. Алгоритм Стратегии 1 повторяется до тех пор, пока ДО не войдет в заданный регион.

1. Регион разбивается на кластеры.
2. Определяются номера кластеров, которым принадлежит цель и ДО.
3. Задается время запаздывания, необходимое вычислительному устройству (ЭВМ) для решения задачи перевода ПМ ДО в целевую точку.
4. ПМ ДО и модель цели продвигаются (путем интегрирования уравнений движения) в точки, соответствующие времени запаздывания.
5. Из указанных точек строятся или одно, или два дерева навстречу друг другу. Дерево из точки ПМ ДО строится с прямым оператором перехода, а из точки нахождения модели цели — с обратным оператором перехода. Алгоритм построения деревьев описывается ниже.

 



6. Решением считается событие состоящее в том, что одному кластеру принадлежат какие либо ВО двух деревьев или, что ВС дерева ПМ ДО и ВС модели цели принадлежит одному кластеру.
7. Размеры региона уменьшаются до размеров кластера, которому принадлежат ВС ДО и цели.
8. Регион снова разбивается на кластеры, но меньших размеров и осуществляется переход к п.3.2.

1. Задается время запаздывания, необходимое вычислительному устройству (ЭВМ) для решения задачи перевода ПМ ДО в целевую точку.
2. ПМ ДО и модель цели продвигаются (путем интегрирования уравнений движения) в точки, соответствующие времени запаздывания. Управляющее воздействие на ДО остается таким, каким оно было на предыдущем цикле вычислений.
3. Задается время прогнозирования.
4. Из точки состояния ПМ ДО прогнозируются два ВС при заданном значении времени прогнозирования для двух постоянных, противоположных по значению управляющих воздействий ВС⁺ и ВС^-.
5. ВС нормируются путем деления их компонент на соответствующие максимально допустимые значения.
6. В нормированном пространстве определяются расстояния между целевой точкой BCg, точками ВС⁺ и ВС^-.
7. Выбирается тот знак управляющего воздействия, которому соответствует меньшее расстояние до целевой точки. Это управляющее воздействие подается на ДО.

Алгоритм перевода динамического объекта (ДО) из начальной точки пространства состояний (ПС) в заданную область пространства, ограниченную интервалами по каждой компоненте вектора состояния (ВС), за минимальное время состоит из следующих шагов:

Ввод исходных данных.

1. Положить значение глобального номера узла .

Вычислить:

ns в бинарной форме ;

число разрядов ,

номер этажа ,

номер узла в этаже ,

код управляющего воздействия в узле ,

число узлов в этаже ,

2. Определить номер родительского узла.

4. Пометить текущий узел как запретный.

7. Определить величину шага tu квантования процесса по управляющему воздействию.

8. По значению глобального номера узла определить знак управляющего воздействия.

1. Либо для детерминированного случая по логической функции,
2. Либо для стохастического случая по пороговому значению вероятности: если да, то перейти к п. 16.; если нет, то перейти к п. 11.

11 .Проверить выполняются ли ограничения, наложенные на ВС

1. Либо для детерминированного случая по логической функции,
2. Либо для стохастического случая по пороговому значению вероятности: если да, то перейти к п. 15.; если нет, то перейти к п. 12.

12. Определить находится ли ВС в пределах заданного ПС

1. Либо для детерминированного случая по логической функции,
2. Либо для стохастического случая по пороговому значению вероятности: если да, то перейти к п. 14.; если нет, то перейти к п. 13.

13. Согласно Стратегии 1 перевести ДО, находящиеся за пределами ПС, в заданный регион, в котором ограничения на ВС выполняются. Определить значение ВС. Перейти кп.1.

14. Определить номер кластера, которому принадлежит ВС и пометить его как запретный. Перейти к п. 1.

15. Определить номер кластера, которому принадлежит ВС, пометить его как допустимый. Выбрать Стратегию 2. Перейти к п.1.

16. Выбрать Стратегию 3.

17. Нет решения. Заново разбить кластерное пространство на кластеры, увеличив их число. Положить и перейти к п.1.

Вычислительный процесс, организуемый в соответствии с приведенным выше алгоритмом, имеет ряд особенностей. Во-первых, он опирается на кластерный анализ, технику комбинаторных и интервальных вычислений [6,7], что, в конечном итоге, дает интервальный (нечеткий) результат и, в свою очередь, порождает дополнительную задачу выбора решения. Во-вторых, при учете случайных воздействий, задача выбора решения приобретает логико-вероятностный характер. Как известно, для нормального стационарного случайного процесса вероятность р попадания случайной величины х в интервал определяется выражением:

где: т - математическое ожидание процесса ; s - среднеквадратическое значение ;

— интегральная функция Лапласа.

Для принятия решения выбирается максимум вероятности попадания случайной величины в заданный интервал.

Ограничения, накладываемые на допустимый объем доклада позволяют лишь схематично очертить круг вопросов, связанных с проблемой логического управления ДО в кластерном пространстве состояний. За пределами доклада остались не описанными алгоритмы вычисления элементов кластерного анализа, концепция логико-лингвистических функций для упрощения процедур принятия решений, результаты имитационного моделирования и оценки эффективности рассматриваемого подхода. По затронутой проблематике эти пробелы авторы восполнят в готовящейся к печати монографии.

ЛИТЕРАТУРА

1. А.Е. Городецкий, В.В. Дубаренко, В.Г. Курбанов. Метод поиска оптимальных управляющих воздействий на динамические объекты с адаптацией к изменениям внешней среды, //6-й Санкт-Петербургский симпозиум по теории адаптивных систем (SPAS'99). СПб., 1999.
2. Д. Табак., Б. Куо. Оптимальное управление и математическое программирование. -М.: Наука, 1975.
3. Юдин Д.Б. Вычислительные методы теории принятия решений. М.: Наука. Гл.ред.физ.-мат.лит.,1989.-320с.
4. А.Е. Gorodetsky, V.V. Dubarenko. Binary trees in state space of dynamic control objects.// First International Conferense on Problems of Dynamic Objects Logic- Linguistic Control DOLLC '97. SPb„ 1997.
5. Рейнгольд Э., Нивергельт Ю., Део Н. Комбинаторные алгоритмы. Теория и практика. Мир. М„ 1980.
6. Алефельд Г., Херцбергер Ю. Введение в интервальные вычисления.-М.: Мир, 1987.
7. Колмыков С.А., Шокин Ю.И., Юлдашев 3.X. Методы интервального анализа. -Новосибирск: Наука, 1986.