НЕЧЕТКИЕ ТЕХНОЛОГИИ УПРАВЛЕНИЯ В ОПТОЭЛЕКТРОННЫХ СИСТЕМАХ

Gorodetzkii A.E., Yerofeyev A.A., Zhuikov A.U.

Russia, St. Petersburg, State Technical University

E:mail: yerofeev@ritz.stu.neva.ru,. Yerofeev@mail.infos.ru

FUZZY TECHNOLOGIES OF CONTROL IN THE OPTOELECTRONIC SYSTEMS

Annotation

There are described the creation of optoelectronic transducers on the base of fuzzy logic. There are considered the perspectives & estimations of these devices operation.

Городецкий А. Е., Ерофеев А. А.*, Жуйков А. Ю.

Россия, С.-Петербург, Санкт-Петербургский государственный технический университет ИПМАШ РАН, СПбГТУ*

E-mail:Yerofeev@ritz.stu.spb.su, Yerofeev@mail.infos.ru

НЕЧЕТКИЕ ТЕХНОЛОГИИ УПРАВЛЕНИЯ В ОПТОЭЛЕКТРОННЫХ СИСТЕМАХ

Аннотация

Рассмотрено построение оптоэлектронных преобразований на принципах нечеткой логики. Представлены перспективы и даны оценки показателей работы таких устройств.

В последние годы получили широкое распространение устройства, работа которых основана на принципах нечеткой логики. В частности, среди устройств такого типа особо выделяются “нечеткие логические регуляторы” (Fuzzy Logic Controller – FLC) [1]. Они применяются во всех областях техники от управления большими технологическими установками (например, доменными печами) до автоматической фокусировки в массовых дешевых фотоаппаратах.

В общем случае логический нечеткий регулятор (НР) состоит из четырех основных блоков: фазификатора, нечеткой базы знаний, машины нечеткого вывода и дефазификатора. Обобщенная структура FLC приведена на рис. 1.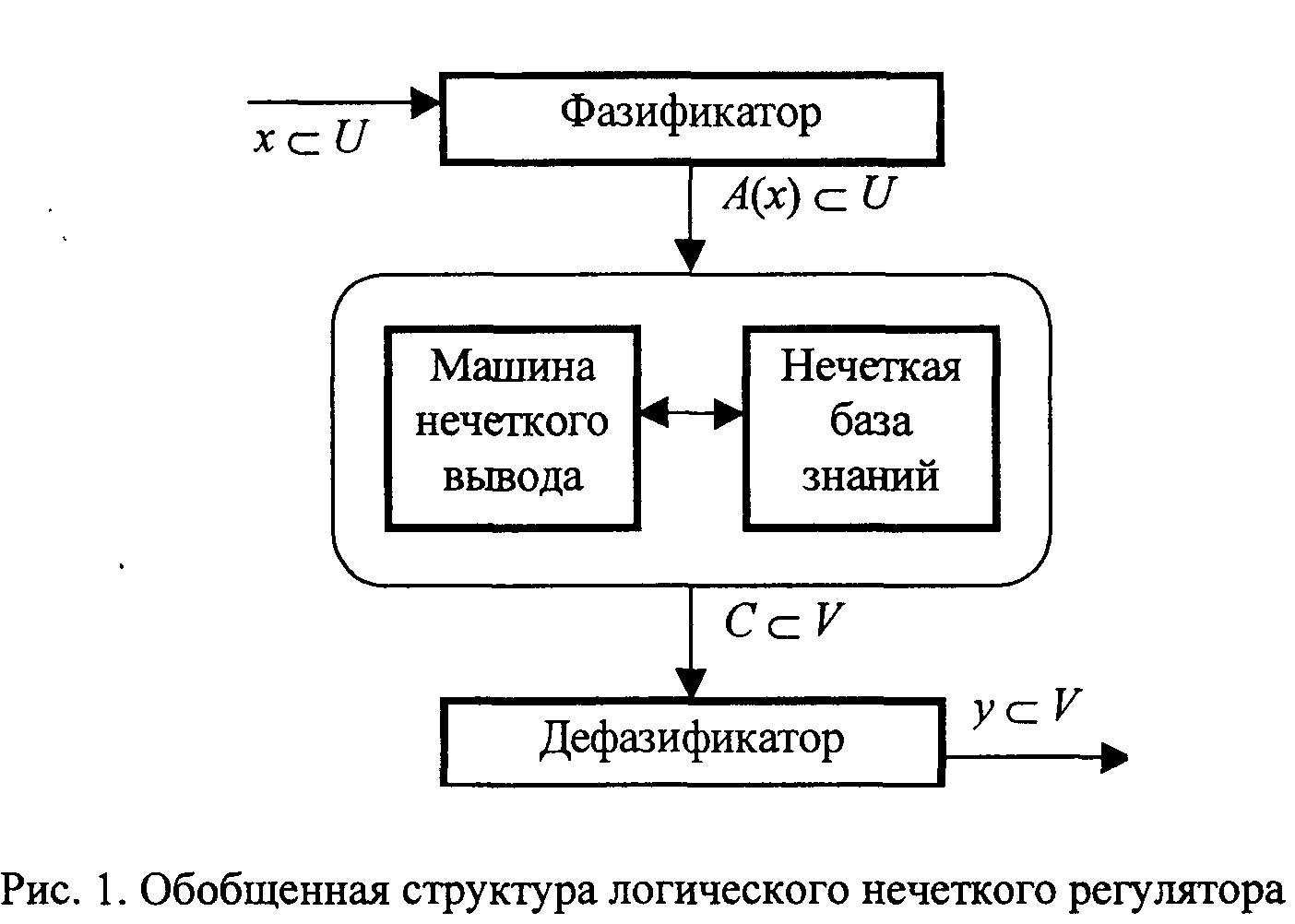

На вход НР поступает “четкая” исходная информация, например вектор входных переменных Фазификатор преобразует эту информацию в нечеткое множество (или нечеткое число) Далее машина вывода на основе нечеткой базы знаний производит обработку входных величин, и полученное нечеткое множество (нечеткое число) с блоком дефазификации отображается в четкую выходную величину y, используемую для управления объектом. В общем случае нечеткий регулятор может содержать ряд фазификаторов, если необходим ввод нескольких параметров, и соответственно, ряд дефазификаторов, если необходимо реализовывать несколько управляющих воздействий на объект.

Четкие входные величины на вход фазификатора поступают, как правило, с аналоговых датчиков, установленных на объекте управления, что требует организации процедуры фазификации в электронном тракте устройства. В ряде случаев можно упростить и ускорить ввод данных в регулятор, применяя новые схемотехнические элементы для непосредственного преобразования физических величин в нечеткие величины (множества). Эти элементы получили название измерительные преобразователи или сенсоры с нечетким выходом — нечеткие сенсоры (fuzzy sensor).

Предположим, что одной из входных переменных для нечеткого регулятора является значение температуры, семантически представляемой в виде лингвистической переменной t , характеризуемой следующим кортежем:

(x, T(x), U, G, M),

где x — имя переменной;
T(x) — множество лингвистических значений (термов) x, каждое из которых соотносится с некоторым нечетким числом, определенным на интервале U;
G — синтаксическое правило для генерации значений x;
M — семантическое правило для лингвистической интерпретации каждого значения.
Например, если температура интерпретируется как лингвистическая переменная, тогда набор термов T (температура) может быть следующим:
T = {очень низкая, низкая, средняя, высокая, очень высокая},
где каждый терм в T (температура) характеризуется нечетким множеством в области значений (в градусах) U = [– 60, 60]. Можно дать следующую конкретную интерпретацию:
очень низкая — “температура значительно ниже минус 20 градусов”;
низкая — “температура примерно около минус 20 градусов”;
средняя — “температура около нуля градусов”;
высокая — “температура примерно около плюс 20 градусов”;
очень высокая — “температура значительно выше 20 градусов”.

Эти термы могут быть охарактеризованы как нечеткие множества, чьи функции принадлежности показаны на рис. 2.

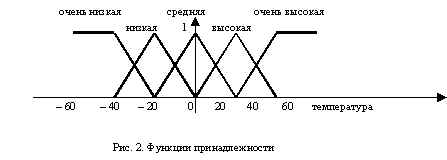
wpe4.jpg (8515 bytes)

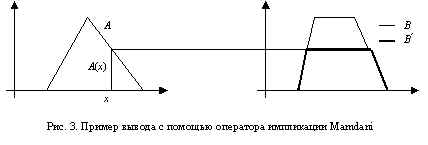
Таким образом, функция нечеткого сенсора — отнесение входной четкой величины x₀ к тому или иному терму, то есть преобразование ее в нечеткое множество A_i. При этом отметим, что требуется получить и величину A_i(x), интерпретируемую как степень принадлежности x к данному нечеткому множеству и необходимую в дальнейшем при обработке нечеткой машиной вывода. Это проиллюстрировано на рис. 3 на примере вывода с помощью оператора импликации Mamdani:

B'(y) = sup{A'(x)ЩA(x)ЩB(y)ЅxОR}, yОR

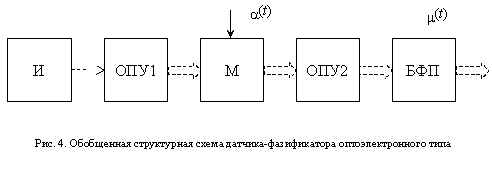
Обобщенная структурная схема датчика-фазификатора оптоэлектронного типа представлена на рис.4.

Схема содержит источник света (И), оптические передающие устройства (ОПУ1, ОПУ2), модулятор (М) и блок фотоприемников (БФП). Источник создает необходимый поток света, выполняющий в оптоэлектронном фазификаторе роль носителя информации. Оптические передающие устройства включены в схему для изменения направления светового потока в целях уменьшения габаритов конструкции. С помощью модулятора измеряемая (преобразуемая) аналоговая величина a (t) вводится в оптический тракт оптоэлектронного фазификатора. Блок фотоприемников служит для преобразования аналогового сигнала переносимого в оптическом тракте лучем света в выходной электрический сигнал. Причем номер фотоприемника в блоке будет соответствовать лингвистической переменной (e ), а напряжение, снимаемое с этого фото приемника — ее функции принадлежности ( m (e ) ).

wpe5.jpg (7642 bytes)

wpe6.jpg (10154 bytes)

Рассмотрим принципиальные оптоэлектронные схемы реализации нечетких измерительных преобразователей. Простейшая дефлекторная схема показана на рис. 5.

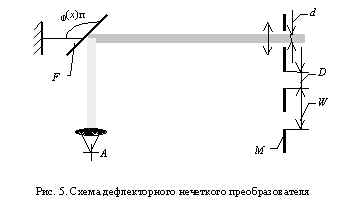
wpe7.jpg (7396 bytes)

Коллимированный луч света диаметром d от источника A отклоняется дефлектором F таким образом, что засвечивает, в зависимости от угла j(x), одно из отверстий маски M. Угол отклонения зеркала дефлектора j является функцией входной величины x. За маской устанавливаются либо фотоприемники, либо оптические элементы канализации света для передачи сигналов (при необходимости — после нормализации) на последующую обработку. Выходной функцией системы является площадь засветки фотоприемника или входной апертуры оптической системы S_i, где i — номер засвеченного отверстия маски. При диаметре отверстий D = d, их шаге W = 1,5D, постоянном расстоянии от дефлектора до маски, квадратных сечениях отверстий и пучка вид зависимости S_i(j), а следовательно, и S_i(x), примет вид, показанный на рис. 6.

Если принять входной сигнал описанной дефлекторной системы, как “четкий” входной параметр x, то площадь засветки каждого отверстия маски S_i, отнесенная к S_max, будет соответствовать величине A(x) (см. рис. 3) для каждого i-го терма. Интерпретируя пример лингвистически, можно сказать, что, если входной величиной x является температура (j = a(t)), то засветка первого отверстия маски будет соответствовать значению температуры “низкая”, второго — “средняя”, и третьего — “высокая” с соответствующими значениями A₁(t) = bS₁(j), где b — некоторый коэффициент.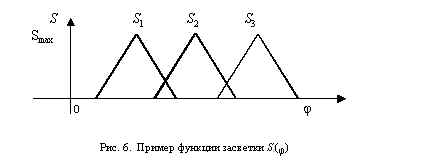

wpe8.jpg (6653 bytes)

Таким образом, в то время, как нечеткое множество определяется множеством кортежей

A = {(x, A(x))|x О X},

вид выходной функции описываемого устройства определяется множеством

S = {(j, S(j))|j О F},

откуда видно, что S можно рассматривать, как некоторый оптический аналог (модель) A, а функцию S(j) — аналог (модель) функции принадлежности.

Соотношения диаметров пучка света d, отверстий маски D и периода их следования W, равно как и форма отверстий и сечения пучка задают вид функции принадлежности. Так, при D > d будет иметь место трапециидальная функция, при сечениях пучка и отверстий, отличных от прямоугольных, вид функции будет близок колокообразному и т. д.

Известно, что функция принадлежности A(t) в общем виде может быть представлена следующим образом: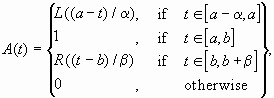

где [a, b] — “пик” или “ядро” A; L:[0,1] ® [0,1], R:[0,1] ® [0,1] есть непрерывные и невозрастающие функции с L(0) = R(0) = 1 и L(1) = R(1) = 0.

Таким образом, изменением геометрических параметров пучка света и маски, а также распределения интенсивности в пучке подбирается вид функций L и R. Более того, используя в качестве маски управляемый транспарант, можно получить устройство с переменной функцией принадлежности, что расширяет функциональные возможности предлагаемой схемы.

Обобщенное математическое описание оптоэлектронных фазификаторов

Базовым объектом описания и анализа метрологических характеристик оптоэлектронных фазификаторов является измерительная процедура, представляющая собой последовательность измерительных преобразований входного воздействия. Степень детализации описания измерительной процедуры определяется числом учитываемых элементарных измерительных преобразований.

На вход измерительного канала поступает смесь сигнала a(t) и помехи e(t): f(t) = a (t) + + e(t). В общем случае измерительная процедура состоит из операций ввода аналоговой измеряемой величины a (t) в оптический тракт, то есть модуляции, передачи оптического сигнала, оптического кодирования, фотоэлектрического преобразования, аналого-цифрового преобразования электрического сигнала для передачи в ЭВМ. Результат измерительных преобразований в аппаратных средствах оптоэлектронного измерительного канала в общем виде в операторной форме можно представить в виде:

y_i^*(t) = R_M* R_у *R_П*R_Д*R_К*R_Ф*f_i(t),

где y_i*(t) — результат, полученный в i-ом измерительном преобразовании; f_i(t) — входное воздействие в i-ом преобразовании; R_M - оператор модуляции; R_у — оператор оптического усиления; R_П - оператор оптической передачи; R_Д — оператор дискретизации непрерывного входного воздействия; R_К — оператор квантования; R_Ф — оператор фотоэлектрического преобразования.

Оператор модуляции можно записать в следующем виде:

где t_g — время дискретизации (преобразования); k_M(t₀ ,tg) — импульсная переходная характеристика модулятора, зависящая от его типа.

Модулятор в оптоэлектронном фазификаторе в простейшем случае это механическая система, обеспечивающая передачу преобразуемого перемещения в перемещение луча определенной формы по блоку фотоприемников (шток, вал, редуктор и т. п.). Это может быть оптико-механическая система, включающая зеркала, линзы и т. п. Однако все типы модуляторов можно считать апериодическим звеном, так как при измерении изменяющихся во времени аналоговых величин, с целью уменьшения динамических погрешностей, аналого-цифровое преобразование производят со скоростью как минимум на порядок больше скорости изменения измеряемой величины. Тогда, если считать, что в процессе измерения входная аналоговая величина практически не изменяется, то оператор модуляции будет равен:

где К_м — передаточный коэффициент модулятора; T_M — постоянная времени модулятора.

При этом, если T_M<< t_g (а это, как правило, так), то:

R_M *f(t) = K_м *f(t) = x_M (t).

2. Оптический усилитель — это растровое сопряжение измерительного (сигнального) растра с неподвижным (опорным). Его можно считать запаздывающим элементом с временем запаздывания, равным:

T_y = l₀ /с₀ ,

где с₀— скорость света в оптическом усилителе; l₀ — длина пути света в оптическом усилителе.

Тогда оператор оптического усиления будет записан как:

R_у *x₀ (t) = К_ус *x₀ (t_g– t_y) = x_y (t_g – t_y),

где Кус — передаточный коэффициент оптического усилителя (коэффициент усиления перемещения).

Обычно t_g << t_y и поэтому можно считать, что:

R_у *x₀ (t) = К_ус * x₀ (t) = x_y (t).

3. Дискретизация непрерывного входного воздействия производится в оптическом кодирующем устройстве (ОКУ) (в описанном выше случае это жидкокристаллическая кодовая маска), которое можно считать элементом с запаздыванием:

t_ОКУ= l_ОКУ/с_ОКУ,

где с_ОКУ — скорость света в ОКУ, l_ОКУ — длина пути света в ОКУ.

Тогда оператор дискретизации можно записать в виде:

R_Д* x_y (t) = x_y (t_g–t_ОКУ).

Обычно t_ОКУ << t_g и поэтому можно записать, что:

R_Д* x_y (t) = x_y (t_g).

4. Оператор квантования в этом случае будет равен:

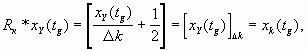
где [ ] — целая часть; D k = fmax /2n — интервал квантования; fmax — максимальное значение воздействия на входе ОКУ или верхняя граница динамического диапазона; n — разрядность ОКУ.

5. Оптическую линию передачи сигнала можно считать элементом с временем запаздывания:

t_св= l_св/с_св,

где с_св — скорость света в оптической линии; l_св — длина пути света в оптической линии.

Тогда оператор оптической линии передачи сигнала будет равен:

R_П *x_k (t_g) = K_CB *x_k (t_g – t_CB) = x_n (t_g – t_CB),

где K_CB — передаточный коэффициент оптической линии. Обычно t_СВ << t_g и поэтому можно считать, что

R_П *x_k (t_g)=K_CB *x_k (t_g)= x_n (t_g).

6. Блок фотопреобразователей можно считать апериодическим звеном и, если можно принять, что за время измерения входное воздействие практически не изменяется, то оператор фотоэлектрического преобразования будет равен:

где K_Ф — передаточный коэффициент блока фотопреобразователей; T_Ф — постоянная времени фотопреобразователей. При этом, если T_Ф<< t_g, то:

R_Ф * x_n (t_g) = K_Ф* x_n (t_g) = x_Ф (t_g).

Можно рассмотреть вид формулы y_i^*для рассмотренных выше оптоэлектронных фазификаторов.

При расчетах дефлекторного фазификатора с блоком фотоприемников на фотодиодах и компараторах формула примет вид:

y_i^*(t) = R_M*R_П*R_Ф*f_i(t).

При расчетах дефлекторного фазификатора с АЦП в оптическом тракте (кодовая маска) формула примет вид:

y_i^*(t) = R_M* R_П*R_Д*R_К*R_Ф*f_i(t).

При расчетах растрового фазификатора с АЦП в оптическом тракте (кодовая маска) формула примет вид:

y_i^*(t) = R_M* R_У*R_П*R_Д*R_К*R_Ф*f_i(t).

Полученные уравнения могут служить основой для проведения метрологического анализа исследуемых оптоэлектронных фазификаторов с определением причин возникновения погрешности.

Статические и динамические характеристики

Статические характеристики фазификаторов соответствуют уравнению в операторной форме, приведенном выше при исключении времени из уравнений коэффициентов передачи.

На рис. 7 приведены обобщенные статические характеристики оптоэлектронных фазификаторов на фотодиодах и компараторах с разными геометрическими формами фотоприемника и луча, засвечивающего этот фотоприемник.

На рис. 7, а представлена статическая характеристика фазификатора в случае, когда луч, засвечивающий фотоприемник, имеет прямоугольную форму, а фоточувствительный элемент — круглую.

На рис. 7, б представлена статическая характеристика фазификатора в случае, когда луч, засвечивающий фотоприемник, имеет прямоугольную форму, а фоточувствительный элемент — треугольную.

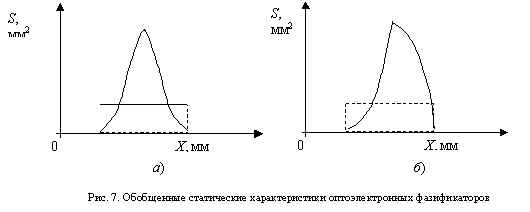
wpe9.jpg (10723 bytes)

Для фазификатора с АЦП в оптическом тракте при использовании жидкокристаллической кодовой маски (ЖКМ) можно получить любую форму статической характеристики (любую форму терма), если запрограммировать ее в ЖКМ в двоичном или ином коде.

Надо отметить, что фазификатор имеет еще одну выходную величину — сигнал лингвистической переменной. Этот сигнал всегда принимает какое-то фиксированное значение, когда засвечивается тот или иной фотоприемник, и отсутствует (равен нулю), когда луч не попадает на тот или иной фотоприемнк (на рис. 7, а, б сигнал лингвистической переменной показан пунктиром).

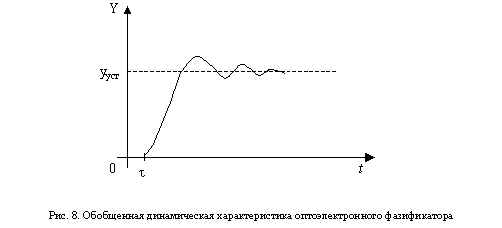
Динамические характеристики фазификатора могут быть получены при подстановке вместо входной величины единичного входного воздействия в уравнения операторов.

При этом в общем виде оптоэлектронный фазификатор всегда имеет в своей структуре два апериодических звена первого порядка — модулятор и фотоприемник, а также звено запаздывания. Время запаздывания t определяется временем, необходимым на передачу светового луча в оптическом тракте фазификатора и складывается из: времени, необходимого для передачи света в оптическом усилителе, времени, необходимого для передачи света в ОКУ и времени, необходимого для передачи света в оптической линии.

В общем виде динамическая характеристика оптоэлектронного фазификатора представлена на рис. 8.

Анализ погрешностей

Любой фазификатор имеет дискретный выход (лингвистическая переменная принимает значения либо 0, либо 1), либо аналоговый (функции принадлежности являются непрерывной аналоговой функцией). Поэтому при анализе погрешностей фазификаторов надо оценивать как точность определения границ области определения {a, b}, так и точность воспроизведения статических характеристик, соответствующих функциям принадлежности.

Характер проявления и причины возникновения погрешностей фазификатора весьма разнообразны. При многократных измерениях по характеру проявления погрешности могут быть разделены на систематические и случайные. Поскольку большинство внешних факторов, действующих на систему, изменяются случайным образом, то систематической погрешностью в данном случае будет отклонение математического ожидания результатов контроля от истинного значения измеряемой величины, а случайной погрешностью — разность между результатом единичного измерения и этим математическим ожиданием.

wpeA.jpg (8612 bytes)

Можно также разделить погрешности оптоэлектронного фазификатора на статические и динамические по условиям их проявления. Статические погрешности, которые имеют место после завершения переходного процесса в элементах схемы, могут быть разделены на три группы:

методические погрешности, обусловленные неточностью знания параметров физических процессов, на использовании которых основывается работа фаззификатора;
инструментальные погрешности, обусловленные неточностью изготовления деталей и узлов;
эксплуатационные погрешности, вызванные изменением внешних условий при эксплуатации.

В фазификаторе информация последовательно передается носителем одного вида к носителю другого вида. Вредное влияние на передачу информации оказывают: различие и неравномерность яркости источника излучения (ИИ), его нестабильность; параметры, характеризующие состояние воздушного тракта; характеристики светового потока, неточность изготовления и установки элементов оптического тракта.

При преобразовании оптического излучения в электрический сигнал, осуществляемом приемником оптического излучения, собственные шумы приемника и фоновое излучение среды также искажают полученную информацию. Далее в усилительно-преобразовательном тракте фазификатора имеют место нестабильность коэффициента усиления, а также погрешности преобразования информации к виду, удобному для дальнейших преобразований.

Технологическими источниками погрешности является неравномерность облученности линз, несимметричность коэффициента пропускания оптического тракта, неравномерность чувствительности преобразователей оптического излучения (ПОИ) по поверхности фоточувствительного элемента, шумы ПОИ.

Эксплуатационными источниками погрешности являются: временная нестабильность напряжения питания, износ и нестабильность изготовления механических деталей, старение ИИ и ПОИ, температурная нестабильность яркости ИИ, температурные деформации механических деталей.

В научно-технической литературе нет данных, достаточных для количественной оценки влияния всех перечисленных источников погрешности (например, нет сведений о нестабильности механического изготовления деталей, несимметричности коэффициента пропускания оптической системы и т. д.). Поэтому на практике учитываются лишь некоторые из этих источников, а остальные оцениваются приближенно.

Практически достижимую точность преобразовательной части фазификатора можно оценить из выражения:

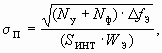
где D f_Э — эквивалентная полоса пропускания тракта преобразования; W_Э— энергетическая чувствительность оптоэлектронных приборов; S_ИНТ — интегральная чувствительность ПОИ; N_У,N_Ф — спектральные плотности усилительной и приемной части.

Если в качестве приемника оптического излучения используется фотодиод, то потенциальная точность равна:

где I_T — темновой ток фотодиода; е — заряд электрона.

Обобщенные показатели качества

Проведенный анализ структур оптоэлектронных фазификаторов и их классификация показали, что одну и ту же физическую величину можно измерить и ввести в память ЭВМ с помощью разнообразных типов оптоэлектронных фазификаторов. Выбор наилучшего варианта структуры, а также составляющих его блоков можно осуществить, исходя из анализа показателей его качества. В информационно-измерительной технике общеприняты следующие основные показатели качества, которые можно использовать для оценки оптоэлектронных фазификаторов: диапазон входных воздействий; максимальное значение абсолютной погрешности; основная приведенная и дополнительная погрешности; допустимое значение диапазона изменения влияющего i-го параметра; приведенная динамическая погрешность второго рода, вызываемая дискретизацией измеряемых сигналов; приведенная динамическая погрешность первого рода, вызываемая инерционностью блоков оптоэлектронных фазификаторов; нелинейность характеристик; минимальное детектируемое воздействие (квант); частотный и динамический диапазоны работы; характеристики надежности, оценивающие вероятность безотказной работы.

Кроме перечисленных, качество оптоэлектронных фазификаторов можно дополнительно оценить следующими специфическими показателями:

собственные потери оптического излучения в фазификаторе, дБ;

индуцированные потери оптического излучения, дБ:

суммарные потери оптического излучения, дБ.

Так же очевидно, что качество оптоэлектронных фазификаторов можно дополнительно оценивать такими общеизвестными показателями, как влагостойкость, устойчивость к вибрациям и ударным механическим воздействиям, долговечность, стоимость, габариты, масса, потребляемая мощность, простота эксплуатации, ремонтопригодность и др.

В ряде случаев удается сформировать обобщенный показатель качества в виде:

где P_i и V_i — i-ый показатель качества и его весовой коэффициент.

Cоответственно, можно сформулировать оптимизационную задачу для синтеза оптимальных оптоэлектронных фазификаторов. Однако в большинстве случаев этого сделать не удается из-за сложности и неопределенности при принятии решения, что требует привлечения экспертных оценок и создания экспертных систем для автоматизации синтеза элементов фазификаторов.

ЗАКЛЮЧЕНИЕ

В настоящее время достаточно полно разработаны основы нечеткого управления, базирующиеся на теории нечетких множеств и лингвистических переменных. Нечеткие регуляторы, как правило, могут быть представлены в виде последовательного соединения блоков фазификаторов, машины нечеткого вывода с базой знаний и дефазификаторов. Нечеткие регуляторы целесообразно использовать только для управления нелинейными объектами. Каждый блок нечеткого регулятора может быть реализован в виде программы, аппаратными или программно-аппаратными средствами. При программной реализации блоков нечеткого регулятора целесообразно использовать специально ориентированные программные средства — фрагменты экспертных систем и реализаций в виде нейронной сети.

Аппаратные средства целесообразно использовать только при небольшом количестве изменяемых величин и применяемых правил логического вывода. Оптоэлектронные средства целесообразно использовать для реализации блока фазификации, так как оптоэлектронный фазификатор обладает наивысшим быстродействием и помехозащищенностью. При анализе динамических характеристик оптоэлектронных фазификаторов, последние могут быть описаны в виде последовательного соединения двух апериодических звеньев первого порядка (модулятор и блок фотоприемников) и звена запаздывания (передача светового потока в оптическом тракте). Вид статической характеристики определяется соотношением формы луча света падающего на фотоприемник и формой светочувствительной площадки фотоприемника. В фазификаторах с АЦП в оптическом тракте (использовании жидкокристаллической кодовой маски) может быть получена любая форма статической характеристики путем записи ее в двоичном или ином коде. В общем случае фазификатор имеет две статические характеристики: первая соответствует лингвистической переменной и является ступенчатой функцией, а вторая определяет вид функции принадлежности. Для анализа качества нечеткого регулятора могут использоваться общепринятые показатели, среди которых наиболее важными можно считать: диапазон входных воздействий, максимальное значение абсолютной погрешности, основная приведенная погрешность, частотный диапазон работы, динамический диапазон работы и характеристика надежности, оценивающая вероятность безотказной работы.

Разработанная в данной работе модель схемы дефлекторного оптоэлектронного фазификатора имеет стандартную структуру. Методика расчета соответствует стандартной методике расчета оптоэлектронных приборов, исключая расчет статической характеристики, соответствующей функциям принадлежности. При расчете статической характеристики для данного класса фазификаторов целесообразно использовать геометрические и тригонометрические соотношения. При анализе погрешностей фазификатора основной погрешностью является погрешность, возникающая из-за перекоса луча засвечивающего фотоприемник. Эта погрешность может возникать при неточном изготовлении и установки элементов оптического тракта и приводит к смещению статической характеристики.

Исследования макета датчика-фазификатора и экспериментальной установки на его основе обнаружили интересную особенность фазификатора, позволяющего путем изменения уровня напряжения, питающего лампу, изменять форму статической характеристики.

ЛИТЕРАТУРА

Guo S., Peters L., Surmann H. Design and application of an analog fuzzy logic controller/ IEEE trans. on fuzzy systems, 1997, v.4, N4, 478рр.
Fuzzy reasoning in information decision/ Ed. Tzafestas Sp.– L.:, Kluwer, 1994 – 567pp.
Leitch R. Knowledge-based control: selecting the right tool for the job // In Artificial intelligence in real-time control, 1992 – Oxford: Pergamon, 1993,v.17, 236рр.
Efstathiou J. Architectures and techniques of artificial intelligence in process control// In Artificial intelligence in real-time control, 1992 – Oxford: Pergamon, 1993, v.17, 348рр.
Expert systems in process control/ D.Rehbein, S.Thorp, D.Deitz etc // ISA Trans., 1992, v.31, N2, 88рр
Lukas M. et al. Evaluation of ES for real-time process management/ In Artificial intelligence in real-time control, 1989 - Oxford: Pergamon, 1990, v.15, pt.2, 124рр
Нечеткие множества в моделях управления и искусственного интеллекта/ Под ред. Д.А. Поспелова – М.: Наука, 1986 – 312с.
Мелихов А.Н., Бернштейн Л.С., Коровин С.Я. Ситуационные советующие системы с нечеткой логикой – М.: Наука, 1990 – 272с.
Ерофеев А.А., Поляков А.О. Интеллектуальные системы управления. СПбГТУ, СПб, 1999 – 265 с.

Site of Information Technologies
Designed by inftech@webservis.ru.