Russia, St.-Petersburg, Institute of Problems of Mechanical of

Russian Academy of Sciences (IPMASH RAS)

E-mail: gae@msa.ipme.ru

The generalized abstract mathematical description of control problems are analysed and classified. The mathematical models of continuous and discrete, linear and non-linear control systems are examined. The stochastic and fuzzy models are picked out especially. The peculiarities of mathematical models of human-machine systems are analysed and fomulated the new problems for behavioral models of decision making person.

Россия, Санкт-Петербург, Институт проблем машиноведения (ИПМАШ РАН),

E-mail: gae@msa.ipme.ru

Анализируется обобщенное математическое описание задачи управления и проводится классификация задач управления. Рассматриваются математические модели непрерывных и дискретных, линейных и нелинейных систем управления. Особо выделяются стохастические и нечеткие модели. Анализируются модели человеко-машинных систем и формулируются новые задачи моделирования поведения лица, принимающего решения.

Процесс распространения идей и методов автоматического управления на все более сложные и плохо формализуемые процессы и структуры типа: гибких автоматизированных производств (ГАП), научно-производственных объединений или социально-экономических образований, — сопровождается постоянным усложнением используемых методов и алгоритмов управления и соответствующих им аппаратных и программных средств. В последнее время интегрированные системы автоматического управления (ИСАУ), используемые для указанных целей, принято строить как магистрально-модульные многоуровневые и многопроцессорные системы с древовидной сетевой архитектурой [1]. Программные средства таких ИСАУ обычно имеют архитектуру открытых систем, использующую принцип модульности программных блоков и независимости от применяемых аппаратных и программных платформ. Примером подобной программной архитектуры может служить система OSACA, разработанная сообществом европейских станкостроительных организаций и предприятий для систем цифрового управления производством [2] .

При создании подробных ИСАУ одним из важнейших этапов является формализация описания объектов управления, среды функционирования, управляющих модулей и систем, а так же целей управления. Процесс формализации обычно начинается с лингвистического описания задачи, построения систем логических уравнений, соответствующих поставленной и описанной лингвистической задачи и отражающих причинно-следственные связи между понятиями и отношениями, определение допустимых решений построенной системы уравнений и поиск наилучших решений путем анализа атрибутов логических переменных, в том числе и таких их качественных элементов, как понятия и отношения с нечеткими границами, высказывания с многозначной шкалой истинности и др. Причем, чем сложнее описываемые объекты, тем более нечеткие описания удается сформулировать на первом этапе. Далее, в процессе анализа задачи и пополнения об объектах за счет проведения дополнительных исследований и изучения аналогов все или часть неопределенностей удается разрешить. При этом если все неопределенности разрешаются, то получаются четкие модели, описываемые системами уравнений с вещественными или комплексными аргументами, а если не все неопределенности разрешаются, то поддаются нечеткие модели, описываемые системами уравнений с логическими и (или) лингвистическими переменными. Исследование последних сопряжено с переборными методами решений, нескалярными целевыми функциями и множественностью оптимальных решений, ранжирование или упорядочивание которых часто носит субъективный характер. Однако; попытки в этом случае решать задачи путем задания строгих границ "волевым" методом или искусственным введением однозначности, приводят к огрублению исходных данных, которое может способствовать получению четкого, но неверного результата, и поэтому нецелесообразны. Следовательно, формализованное описание ИСАУ может быть двух классов четкое и нечеткое. В последнем случае управление принято называть нечетким (fuzzy control) [3].

В общем случае задача управления может быть охарактеризована следующим кортежем:

(1)

где: Z — множество альтернативных решений,

М — окружение выбора, т.е. среда задачи, в которую включены эталонная модель объекта управления, технических средств его осуществления и окружающей среды, в которой предполагается функционирование управляемого объекта.

Р — система предпочтений эксперта или системы, принимающей на базе которой строятся критерии качества К, соответствующие целям управления Q,

W — необходимые способы действий (алгоритм), которые требуется выполнить над множеством альтернатив Z, например найти наиболее предпочтительную, линейно упорядочить множество допустимых альтернатив и т. п., для того, чтобы управление объектом удовлетворяло системе предпочтений Р по построенному критерию качества.

Альтернативным решением будем называть вариант решения, удовлетворяющий ограничениям задачи управления и обеспечивающий получение требуемых параметров и характеристик управления, а средой задачи — эталонную модель объектов и системы управления, я же тех условий, в которых предполагается функционирование ИСАУ, которые необходимо учитывать при формировании и решении задачи. При этом можно выделить следующие пять основных типов задач управления:

— в условиях определенности, когда каждой альтернативе соответствует строго определенный исход,

— в условиях риска, когда исход является дискретной или случайной величиной с известным законом распределения или, хотя бы, с известными числовыми характеристиками распределения,

— в условиях неопределенности, когда исход является логической переменной функцией с известной вероятностью ее истинности ложности,

— в условиях неопределенности, когда исход является лингвистической переменной, задаваемой кортежем , где I — наименование лингвистической переменной, L — множество ее значений или термов, представляющих собой наименование нечетких переменных, областью определения из которых множество A, G — синтаксическая процедура, описывающая процесс образования из множества L новых, осмысленных для данной задачи значений лингвистической переменной, V — семантическая процедура, позволяющая приписать каждому новому значению, образуемому процедурой G, некоторую семантику путем формирования соответствующего нечеткого множества, т.е. отобразить новое значение в нечеткую переменную,

— в условиях неопределенности, когда исход является результатом эволюции и скрещивания ряда альтернатив, каждая из которых может иметь исход либо в виде случайной логической переменной (функции), либо в виде лингвистической переменной.

Первую задачу будем называть классической задачей детерминированного управления, вторую — классической задачей недетерминированного управления, третью — задачей логико-вероятностного управления, четвертую — задачей логико-лингвистического управления и пятую — задачей эволюционно-генетического управления. Очевидно, что к задачам нечеткого управления (ЗНУ) относятся задачи с третьей по пятую и в общем виде их решением будет синтез алгоритма управления из множества альтернатив Z на основе оценок качества К, построенных с учетом системы предпочтений Р и среды задачи М:

, где — обозначает множество всех подмножеств Z, а — множество всех кортежей из К длиной от 2 до .

При формировании эталонных моделей объектов и систем управления возможны различные варианты их математического описания.

Описываются линейными уравнениями состояния вида;

(2)

где; у — п-мерный вектор управляемых параметров,

u — m-мерный вектор управляющих воздействий,

g — r-мерный вектор контролируемых возмущений,

f — k-мерный вектор неконтролируемых возмущений,

А — -мерная постоянная матрица,

В — -мерная постоянная матрица,

С — -мерная постоянная матрица,

D — -мерная постоянная матрица,

К таким системам применим принцип суперпозиции и поэтому можно действия на систему векторов u, g, f изучать раздельно. Это явилось следствием того, что подобные системы описываются обычно уравнением вида:

(3)

Ограничения в таких системах так же линейны:

(4)

(5)

где: s, h — линейные векторные Функции.

Соответственно и целевая функция таких систем должна быть линейной:

(6)

где Y — линейная скалярная функция. Обычно целевая функция в этих системах является показателем качества, выражаемым скалярной величиной вида

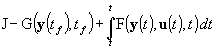(7) .

где G и F — скалярные функции, а и — начальный и конечный моменты времени соответственно

Случаи, когда ограничения и (или) целевая функция нелинейны, относятся к непрерывным нелинейным системам, а случаи, когда целевая функция векторная — относятся к интеллектуальным нечетким системам.

Аналитическое решение уравнения состояния (3) известно и поэтому формализация описания ИСАУ в этом виде является наиболее предпочтительным, но, к сожалению, редко достижимым.

Описываются системой нелинейных обыкновенных дифференциальных уравнений первого порядка вида

, (8)

где — п-мерная нелинейная векторная функция.

В этом случае функции s, h и Y в уравнениях (4 – 6) могут быть нелинейными.

Аналитического решения уравнения вида (8) получить, как правило, не удается. Однако существует достаточно обширный класс систем, для которых удается получить численные решения достаточной точности за приемлемое число итераций.

При постоянном временном интервале могут быть описаны следующей системой разностных уравнений состояния:

, (9)

где k+1 и k — номера интервалов времени.

Вектор состояния у в любой дискретный момент времени может быть определен в виде функции начального состояния и всех предшествующих векторов управления:

(10)

Ограничения в каждый дискретный момент времени имеют вид:

(11)

, (12)

где: , — линейные векторные функции.

Целевая функция принимает вид:

, (13)

где F — скалярная линейная функция.

Формализованное описание дискретных ИСАУ в этом виде наиболее желательно, так как задачу синтеза оптимального управления в этом случае обычно можно свести к задаче линейного программирования [ 4] .

Описываются следующими разностными уравнениями состояния

, (14)

где — номер временного интервала.

В каждый дискретный момент времени система должна быть подчинена дополнительной системе ограничений;

(15)

(16)

где , — в общем случае нелинейные функции.

В этом случае функция F в уравнении (13) для целевой функции может быть нелинейной. Аналитического решения система (14) в общем случае не имеет. Однако существует класс систем, для которых можно получить достаточно точные численные решения.

В задачах недетерминированного управления стохастические объекты и системы можно описывать непрерывными и дискретными линейными или нелинейными моделями, подобными предыдущим. Однако уравнения состояния, ограничений и целевых функций в этом случае записываются для статистических оценок параметров, наиболее используемыми из которых являются оценки математических ожиданий и дисперсий. Кроме того, в этих задачах широко используются такие характеристики входных воздействий и выходных реакций объектов, как корреляционные функции и спектральные плотности случайных функций времени.

6. Нечеткие модели.

В задачах нечеткого управления обычно можно выделить подсистемы, имеющие четкие описания и модели всех рассмотренных выше типов, и подсистемы, имеющие нечеткие описания и модели логико-вероятностного, либо логико-лингвистического типа. Нечеткие описания характерны для интеллектуальных и человеко-машинных систем. Неприятной особенностью таких систем является векторность целевой функции. Последнее требует нетрадиционных подходов к решению оптимизационных задач управления, имеющих высокую сложность и. как правило, размерность.

Логико-вероятностная модель может быть описана системой уравнений вида линейной последовательностной машины [ 5] .

(17)

(18)

где: , — вектора логических переменных принимающих значения 0 либо 1 и характеризующие состояние системы в и моменты времени соответственно,

— вектор логических переменных, принимающих значения 0, либо 1 и характеризующих управления в k момент времени;

— вектор логических переменных принимающих значения 0. либо 1 и характеризующих выход системы в k момент времени,

А, B, C, D — постоянные матрицы из 0 и 1;

, — векторы из 0 и 1,

— знак операции логического умножения матрицы на вектор;

— знак операции сложения по модулю 2

При использовании вычислительных методов анализа подобных систем и синтеза оптимальных решений обычно уравнения (17) и (18) можно заменить уравнением вида [5]:

(19)

где , — постоянные матрицы из 0 и 1, — знак операции суммирования по модулю 2.

Вероятность каждой i-ой компоненты вектора может быть определена через вероятности всех i-ых компонент вектора по полиномиальной формуле [ 6] :

(20)

где: n — размерность векторов и , a N — порядковый номер члена полинома.

Как показано в [ 6] , в большинстве случаев можно получить достаточную точность вычисления , используя всего 5–7 первых членов полинома (20), что существенно облегчает поиск решений с максимальной вероятностью, т.е. решение оптимизационных затрат.

Таким образом, логико-вероятностная модель нечеткой подсистемы может быть описана системой уравнений (19) и (20). Тогда целевая функция будет:

(21)

Поэтому при изменении во времени вероятностей событий такая целевая функция так же изменяется во времени. Последнее обстоятельство является характерной чертой систем управления эволюционно-генетического типа.

Логико-лингвистическая модель нечёткой системы может быть так же описана системой уравнений вида (17), (18). Но при этом каждой логической переменной, т.е. каждой компоненте векторов , ставится в соответствие функция принадлежности заданного вида, область значений которых лежит в диапазоне от 0 до 1. Правила вычисления функций принадлежности для различных логических операций обычно задаются алгоритмически, либо аналитически на основании предыдущего опыта либо обучения системы, т. е. без доказательства их применимости в тех или иных условиях. Последнее может привести к неадекватности модели реальной системе логико-лингвистического типа при изменяющихся условиях.

Таким образом, представляется целесообразным при формализации описания нечетких систем попытаться выделить в них четкие подсистемы того или иного типа и нечеткие подсистемы, описываемые логико-вероятностными моделями. Обычно к четкому описанию можно свести системы управления, целями которых являются стабилизация, программное управление, слежение или самонастройка. Если целями системы управления является целесообразное поведение или живучесть сложной системы, то четкого формализованного описания, как правило, получить не удается. Однако и в таких системах управления обычно можно выделить подсистемы стабилизации, программного управления, слежения и самонастройки, которые удается описать как четкие.

Формирование управляющих сигналов в нечетких системах связано с нечетким принятием решения, которое предполагает, как правило, достижение некоторой цели или, по крайней мере, последовательное приближение к некоторому наиболее предпочтительному варианту (эталону). В нечетких системах управления логико-вероятностного типа целью может быть выбор путем логического вывода наиболее предпочтительного решения, имеющего наибольшую вероятность из всех альтернативных решений. При этом в зависимости от сложности задачи управления и системы могут с большим или меньшим успехом использоваться различные вычислительные методы принятия решения, среди которых наиболее продвинутыми являются математическое программирование и многошаговое обобщённое математическое программирование [ 3] .

При решении рассмотренных выше задач вероятности событий, являющихся логическими переменными задач, считаются постоянными. Однако тогда не учитываются особенности характера человека, либо коллектива людей, принимающих решения в человеко-машинных системах в условиях не полной определённости. Эти особенности заключаются в том, что в процессе умозаключения, т. е. анализа логического правила уверенность в правильности вывода, т. е. вероятность логического вывода может меняться. Например, если появляется событие в момент времени с вероятностью , то лицо, принимающее решение (ЛПР) в момент времени полагает, что, если есть событие , то должно быть сгенерировано событие с вероятностью

(22)

Тогда, если при изменении Т изменяется и , то соответственно меняется и вероятность генерируемого события:

(23)

В процессе рассуждений и умозаключений вероятность вывода у ЛПР может меняться в силу неосознанного, либо осознанного учёта ряда дополнительных факторов. Осознанные факторы можно учесть путем введения их в логико-вероятностные модели в виде дополнительных логических переменных и уравнений. Неосознанные факторы невозможно учесть таким образом. Поэтому естественной возможностью их учёта может быть введение тех или иных, линейных или нелинейных зависимостей от времени вероятностей импликаций. Наиболее простыми являются следующие зависимости

1 при

при

2. при

при

3.

4. при

при

5. при

при

Вопрос использования той или иной зависимости при моделировании поведения ЛПР пока остаётся открытым и требует серьёзных статистических исследований поведения ЛПР в тех или иных условиях. Однако не учет зависимости вероятности принятия решения от времени хотя и облегчает задачу, но может существенно исказить результат, связанный с выбором решения с наибольшей вероятностью на момент принятия решения.

Помимо рассмотренной ситуации при принятии решения ЛПР может быть случай, когда в процессе рассуждений и умозаключений вероятность вывода у ЛПР меняется в зависимости от изменения во времени, каких-либо факторов , которые сами непосредственно невозможно учесть путем ввода их в модель в виде дополнительных логических переменных и (или) уравнений. В этом случае можно записать, что'

(24)

где — вектор влияющих на вероятность импликации факторов

При этом зависимость может быть так же линейной и нелинейной, падающей, растущей, либо колебательной в зависимости от типа характера

Возможен случай, когда требуется учитывать зависимость вероятности импликации, как от времени, так и от вектора влияющих факторов . Ситуация с выявлением зависимости еще более усложняется, если ЛПР является коллективным. Вполне вероятно, что в некоторых случаях эта зависимость становится сингулярной, что может означать потерю управляемости из-за невозможности принятия решения.

Таким образом, среди моделей нечетких систем логико-вероятностного типа можно выделить класс моделей, учитывающих поведение ЛПР. Модели этого класса можно разбить на следующие типы:

• с зависимостью только от времени,
• с зависимостью только от вектора влияющих факторов,
• с зависимостью от времени и от вектора влияющих факторов.

В свою очередь каждый из этих типов может иметь зависимость падающего типа, растущего, колебательного или сингулярного. При этом первые две зависимости могут быть как линейными, так и нелинейными.

Таким образом, при формализации задач управления сложными динамическими системами последние можно разбить на подсистемы, описываемые моделями разного уровня сложности и соответственно всю задачу разбить на ряд вложенных друг в друга подзадач, для решения каждой из которых могут быть использованы предназначенные для них методы и средства. При этом нечёткие задачи являются наиболее сложными, особенно в случае управления в человеко-машинных системах.

В зависимости от решаемого типа задачи можно с большим или меньшим успехом использовать готовые вычислительные алгоритмы математического программирования и соответствующие инструментальные программные средства, среди которых в настоящее время широко используются нейронные сети и системы A-life.

Логико-вероятностные модели с непостоянными вероятностями импликаций, являясь сложными динамическими линейными или нелинейными системами, могут оказываться устойчивыми, либо неустойчивыми и это является их главной отличительной чертой.

Вопрос моделирования поведения коллективного ЛПР является в настоящее время наиболее актуальным и трудным. Однако его решение позволит, наконец, формализовать задачу поиска оптимального коллективного ЛПР. Очевидно, что решение подобным образом задач для различных социально-экономических систем, которые можно отнести к наиболее сложным человеко-машинным системам, является одной из важнейших задач современного общества, ищущего оптимальные пути устойчивого развития.

Литература

1. Городецкий А. Е., Тарасова 1-1. Л. Интегрированные системы автоматизации НИОКР./ Учебное пособие. Изд. СПбГТУ, СПб, 1998.
2. Городецкий А. Е., Тарасова И. Л. Система открытой архитектуры OSACA для интеллектуального управления автоматическими линиями, сложными машинами и системами машин./ Физическая метрология под ред. Городецкого А. Е. Изд. СПбГТУ, 2000
3. Городецкий А. Е. Вычислительные методы нечёткого проектирования./ Вычислительная техника, автоматика, радиоэлектроника. Труды СПбГТУ, №472, СПб, 1998, с. 49–60.
4. Табак Д., Куо Б. Оптимальное управление и математическое программирование / Изд. Наука, М., 1975.
5. Городецкий А. Е., Дубаренко В. В., Ерофеев А. А. Алгебраический подход к решению задач логического управления / А и Т, № 2, 2000.
6. Городецкий А. Е. Дубаренко В. В. Комбинаторный метод вычисления вероятности сложных логических функций./ ЖМВ и МФ, 1999, том 39, № 7, с. 1246–1248.