In this paper VSS with time-delay in phase variables are considered. Parametrical conditions of existence of sliding modes with linear switching function in VSS with standard law of control are lead. Not using complex and diffucult of realization of standards elements of automotica of switching functional that is not using non-standard control laws, wide functional scope of standard algorithms control is shown: The arizen diffuculties because of delay of the effect of delay of in a stable system analysis are borne down by the right choosing of the V - functional Lyapunov-Krasovski method in form “Full quadratic form of variables diffirence plus integral from quadrata of delay term.”

(Истанбульский Технический Университет, Истанбул)

В работе [1] рассмотрены две задачи анализа и синтеза СПС второго порядка с запаздыванием в фазовых координатах. Детальное изучение таких систем имеет важное практическое значение.

В первой задаче рассматриваются стационарная система с запаздыванием начальное множество :

(1)

и управляющее воздействие в виде

(2)

с линейной функцией переключения

,

где а₀, а₁, a ₀ , a ₁ - постоянные параметры объекта управления, с₁ ,k - положительные постоянные.

Сначала изучается частный случай системы (1)-(3) при , в пространстве

V- функционал Ляпунова-Красовского выбирается в виде

(5)

где e > 0 и доказывается следующая теорема об асимптотически устойчивости нулевого решения системы (4), (2):

Теорема1. Пусть для системы (4),2) выполнены следующие неравенства

Тогда нулевое решение системы (4), (2) асимптотически устойчиво в целом.

Сразу же заметим, что вопрос организации скользящих режимов в системе (4) с управлением (2) остался открытым. Более того, покажем, что в системе(4) с управлением (2) невозможно параметрически выписывать условия возникновения скользящих режимов.

Действительно, как это обычно делается как и в классической теории СПС [2] , так и в современной [3], рассмотрим условия возникновения скользящих режимов[3,4]

(7)

Вычисление условий (7), с учетом второго уравнения системы (4) и уравнения (2), приводит к неравенствам

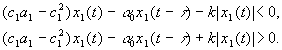
Наличие второго члена в этих неравенствах затрудняет параметрически точно выписывать условия выполнения неравенств.

Заметим, что при неравенство является условиями возникновения скользящих режимов в СПС без запаздывания [4].

Внимательное изучение предыдущих неравенств подсказывает, что для синтеза системы в законе управления (2) явно чего-то не хватает.

Попробуем сформировать управление в виде (лишь добавляя член k_{0 [} x₁(t-)] , естественный для систем с запаздыванием):

(8)

где .

Вычислив производную по времени s в системе (4),(8):

(9)

выясним условия существования скользящих режимов.

Из условий (7) имеем

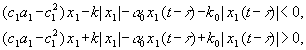
из которых следует, что

Следовательно, при выполнении неравенств (10) в системе (4),(8) возникают скользящие режимы.

Таким образом, получена

Теорема 2. Пусть для системы (4) с управлением (8) выполнены неравенства (10), тогда в СПС с запаздыванием возникают скользящие режимы.

Снова заметим, что условия существования скользящих режимов для СПС с запаздыванием хорошо согласуются с аналогичными условиями для систем без запаздывания [4].

Выясним условия попадания на плоскость скольжения . Согласно методу эквивалентного управления [3] приравниваем производную к нулю при s=0 и находим из второго уравнения системы (4) эквивалентное управление Снова подставляя в (4) имеем уравнения движения системы в скользящем режиме

(11)

Из (11) следует, что необходимым и достаточным условием асимптотической устойчивости движения системы (4) по плоскости s=0 при является . А достаточным условием попадения будет .

Полученные условия для системы с запаздыванием (4) также хорошо согласуются с аналогичными условиями попадания и устойчивости для системы без запаздывания [2,3].

Теперь, исследуем задачу устойчивости нулевого решения системы (4) с управлением (8).

Используя фундаментальные результаты об устойчивости Ляпунова-Красовского [5,6] построим V- функционал Ляпунова-Красовского в виде “неполная квадратичная форма плюс интеграл от квадрата запаздывающего члена”, систематически использованные для СПС с запаздыванием в ранних работах [7-11].

Вычислим производную по времени V- функционала (5) на решениях системы (4) с новым законом управления (8) и после некоторых преобразований сгруппируем в виде

(12)

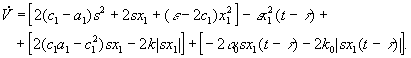
Очевидно, что при выполнении следующих неравенств

(13)

становится определенно-отрицательной. Тогда, как V определенно-положительный. Следовательно, нулевое решение системы (4) с управлением (8) ассимптотически устойчиво в целом. Таким образом, формулируется

Теорема 3. Пусть для системы (4),(8) выполнены неравенства (13),(14), тогда нулевое решение системы(4),(8) ассимтотически устойчиво в целом.

Заметим,что условия устойчивости (13),(14) также включают в себя условия существования скользящих режимов(10).

С целью сравнительного анализа результатов теоремы 1[1] и теоремы 3 перегруппируем члены в правой части (12) в следующем виде

(12а)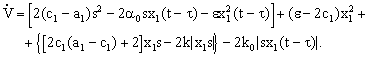

очевидно, что неравенства

(13a)

или же после исключения e :

(14а)

обеспечивают определенно-отрицательность . Следовательно, при выполнении (14а), которые полностью идентичны с условиями (6) для системы (4) с укороченным стандартным управлением (2)[1], система (4) с неукороченным стандартным управлением (2) асимптотически устойчива. Вместе с тем, как мы выше отметили, с помощью укороченного стандартного управления (2) в системе (4) невозможно организовать скользящие режимы.

Во второй задаче в работе [1] рассматривается система (1) в фазовом пространстве x₁,s:

(15)

Отмечается, что если отказаться от первого требования теоремы 1, то система становится неустойчивой. Принимается, что

(16)

но при этом

(17)

Дальше за счет выбора более сложного управления с функционалом переключения, так называемого нестандартного управления [1]:

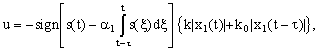
исследуется задача устойчивости системы(15).

Выбирая V - функционал в виде

(19)

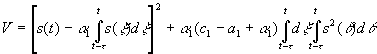
в работе [1] утверждается, что при выполнении следующих неравенств:

(20)

(21)

а также условий (16),(17), система (15),(18) обладает свойством устойчивости.

Заметим, что условия (16),(17),(20), (21), (22) накладывают весьма жесткие ограничения:

(23) или же 0<t a ₁<1) ,

на параметры объекта управления, в том числе на величины постоянного запаздывания t . А это не только желательно, но и не допустимо, поскольку параметры объекта от конструктора системы управления не зависят. Следовательно, требование (20) теоремы 2[1] выполняется лишь в слишком узком диапазоне. По этой причине речь идет только об устойчивости в ограниченной области параметров. Кроме того, при доказательстве теоремы 2[1] используются приближенные оценки (по теореме о среднем) типа, т.е. допускаются малости постоянного запаздывания (сверх того, что) и они входят в ограничение (20). Такое вхождение и оценки помимо всего прочего не свойственны методам исследований с помощью V - функционала Ляпунова-Красовского. В работе [1] отмечается, что: ”Для создания скользящего режима в системе (1) вдоль плоскости s=0 используем в этом управлении функционал переключения”. Однако, вопрос существования скользящих режимов с таким сложным функционалом переключения остался и во второй задаче открытым. Тогда не ясно ради чего используется без особой надобности (хотя и не совсем правильно) такой сложный функционал переключения.

Следует также отметить, что техническая реализация такого сложного функционала переключения (18) с вычислением определенного интеграла с нижними и верхними пределами, на конечных элементах автоматики [12] к настоящему времени весьма сложна и по-видимому, практически невозможна.

Таким образом, при формулировке и доказательстве теоремы об устойчивости системы (15) со сложным и труднореализуемым функционалом переключения, причем без функционирования скользящих режимов, принимаются во внимание противоречивые и неестественные ограничения, допущения, оговорки, а также приближенные оценки и излишне очень сложный функционал переключения.

Теперь, рассмотрим ту же самую систему (15) без использования сложного функционала переключения и откажемся от каких-либо искусственных ограничений на параметры объекта управления, типа таких, как (16), (17),(22),(23).

Применяя классические каноны теории СПС [2] решим вторую задачу синтеза не прибегая к сложному и труднореализуемому функционалу переключения, приводившему к выполнению искусственных ограничений на параметры объекта управления.

Сформируем закон управления в виде (8).

Сначала выясним вопрос существования скользящих режимов в системе (15),(8) по плоскости s=0.

Из (15),(8) запишем

(24)

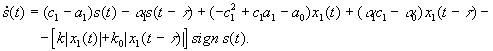
Заметим, что изучение вопроса существования скользящих режимов в системах с запаздыванием стандартными средствами затруднительно и требует особой тщательности.

Выберем V - функционал Ляпунова-Красовского в виде “неполная квадратичная форма плюс интеграл от квадрата запаздывающего члена”:

(25)

Вычислим производную по времени V вдоль траекторий (15),(8)

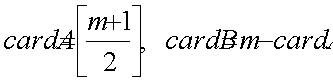
Первые три слагаемые в (26) будем рассматривать как квадратичную форму относительно переменных и сделаем ее определенно-отрицательной.

По критерию Сильвестера

(27)

А остальные слагаемые попарно становятся определенно-отрицательной при выполнении неравенств

(28)

.

Следовательно . Тогда в системе возникают скользящие режимы.

Заметим, что условия устойчивости (27),(28),(29) одновременно являются условиями устойчивости скользящих режимов вдоль s=0 . Итак, получена

Теорема 4. Плоскость s=0 для системы (15), (8) будет плоскостью устойчивого скольжения при выполнении условий (27),(28),(29).

Аналогично первой задаче выясним условия попадания. Естественно обобщая метод эквивалентного управления [3] на системы с запаздыванием при s( t ) =0, находим из (15) эквивалентное управление

(30)

Заметим, что в эквивалентное управление также входит функция переключения с запаздыванием. При формировании и технической реализации такого закона, по-видимому, требуется введение “упредителя Смита” [13] или ее схемной разновидности [11] в контур управления. Повторно подставляя (30) в (15) получаем снова уравнения (11), описывающие движения системы (15),(30) по плоскости скольжения S=0. Тогда, условиями теорем устойчивости и попадания [3] и для системы с запаздыванием (15),(30) будут c_{1 >} 0, c₁-а_{1 <} 0, соответственно.

Настроечные параметры регулятора c₁, k, k₀ и свободные постоянные V - функционала Ляпунова-Красовкого должны подбираться, таким образом, чтобы в системе (15),(18) гарантировалась асимптотическая устойчивость в пространстве x₁,s.

С этой целью выберем среди кандидатов V - функционала Ляпунова-Красовского в отличие от ранних работ [7-11] и [1] в новом виде “полная квадратичная форма разности переменных плюс интеграл от квадрата запаздывающего члена”:

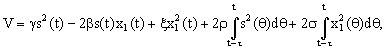
где-свободные положительные постоянные.

Потребуем, чтобы выполнялись условия:

(32) ,

тогда V>0.

Вычислим производную V на решениях системы (15),(8) и используя приемы и методы исследования V -функционала Ляпунова-Красовского для СПС с запаздыванием, систематически использованные в работах [7-11] перегруппируем правую часть в виде:

(33)

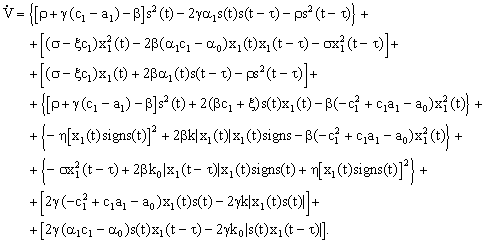
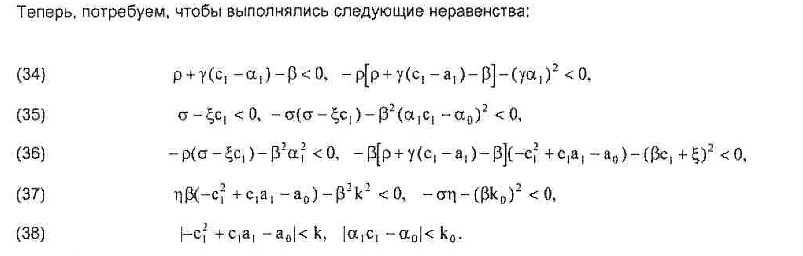
Теорема 5. Пусть для системы с запаздыванием в фазовых координатах (15) и со стандартным законом управления с линейной функцией переключения (8) выполнены условия (27)-(29) теоремы 4 существования скользящих режимов и неравенства (34-38). Тогда нулевое решение СПС с запаздыванием (15),(8) асимптотически устойчиво в целом.

Замечание1. Теорему 5 можно распространить на более общие системы с одним (SISO):

и многими входами (MIMO):

для синтеза законов управления СПС с линейными функциями переключений.

Следует сказать, что теория СПС с запаздыванием с формированием скользящих режимов на функциях или функционалах переключений в последние годы интенсивно разрабатывается в работах многих авторов [14-25].

С П И С О К Л И Т Е Р А Т У Р Ы