 |
||
Agafonov E.D., Ikonnikov O.A., Kuznetsova O.V., Pupkov A.N., Sergeeva N.A.
Russia, Krasnoyarsk,
Research Institute For Control Systems, Wave Processes and Technologies,
Krasnoyarsk State Technical University, Siberian Aerospace Academy,
e-mail: e_agafonov@yahoo.com
NON-PARAMETRICAL MODELS IN INTELLECTUAL IDENTIFICATION SYSTEMS
In the report identification problems in the broad sense are described. This statement of the task assumes lack of model structure search up to parameter vector. This is caused by the fact, that in a number of applications there is no necessary amount of a priori information for the model parametrization. Asymptotic behavior of certain non-parametrical algorithms is studied and results of numerical experiments are described as well.
Агафонов Е.Д., Иконников O.A., Кузнецова О.В., Пупков А.Н., Сергеева Н.А.
Россия, Красноярск,
Научно-исследовательский институт систем управления, волновых процессов и
технологий, Красноярский государственный технический университет,
Сибирская аэрокосмическая академия,
e-mail: e_agafonov@yahoo.com
НЕПАРАМЕТРИЧЕСКИЕ МОДЕЛИ В ИНТЕЛЛЕКТУАЛЬНЫХ СИСТЕМАХ ИДЕНТИФИКАЦИИ
В докладе рассматриваются проблемы идентификации в широком смысле. Подобная постановка предполагает отсутствие выбора структуры модели с точностью до параметров. Это обусловлено тем, что во многих практических задачах отсутствует необходимый объем априорной информации для параметризации модели. Исследованы асимптотические свойства соответствующих непараметрических алгоритмов и изложены результаты численного исследования.
Informational technologies of modeling and control have recently become widely used for industrial purposes. This happened mostly because of their role in increasing of information handling rates and effective control of technological processes. It is natural to expect further development of automation and control computerization for discrete- continuous processes.
Informatization of control processes demands identification problem solution. The most common problem nowadays is identification problem in the narrow sense, i.e. when the task is divided into two steps. The first one involves choosing a model class up to parameters vector, the second one is further estimation of these parameters basing on observation of input and output values with random errors. Identification theory in the broad sense is the least advanced now. The main feature here is the impossibility to define a class of parametrical models because of little a priori information, but the type of operators describing process under research is known. This work is directed to the solution of linear dynamic processes identification in the broad sense.
Statement of the problem is given by Fig.1. Here u(t), x(t) are
input and output variables of the process (object),![]() - certain values of process variables, which be further denoted as
- certain values of process variables, which be further denoted as ![]() .
. ![]()
![]()
![]() - random signals in the measurement channels, appearing in discrete
moments t and having zero mean value and limited deviation.
- random signals in the measurement channels, appearing in discrete
moments t and having zero mean value and limited deviation.
It is known that linear dynamic system (LDS) response to an input signal u(t) is described by Duhamel (or convolution) integral. Finding the output value x(t) is possible if unit impulse response function is known.
The matter of the approach being offered to identification problem solution for described objects class is to use non-parametrical unit impulse response estimations. This lets us not to choose a priori an order of model equation describing object under research (identification in the broad sense) [1,2]. Basis for unit impulse response evaluation will be output values of the system when input has certain standard form. Duhamel (or convolution) integral with non-zero initial values has the following form:
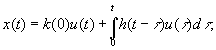 (1)
(1)
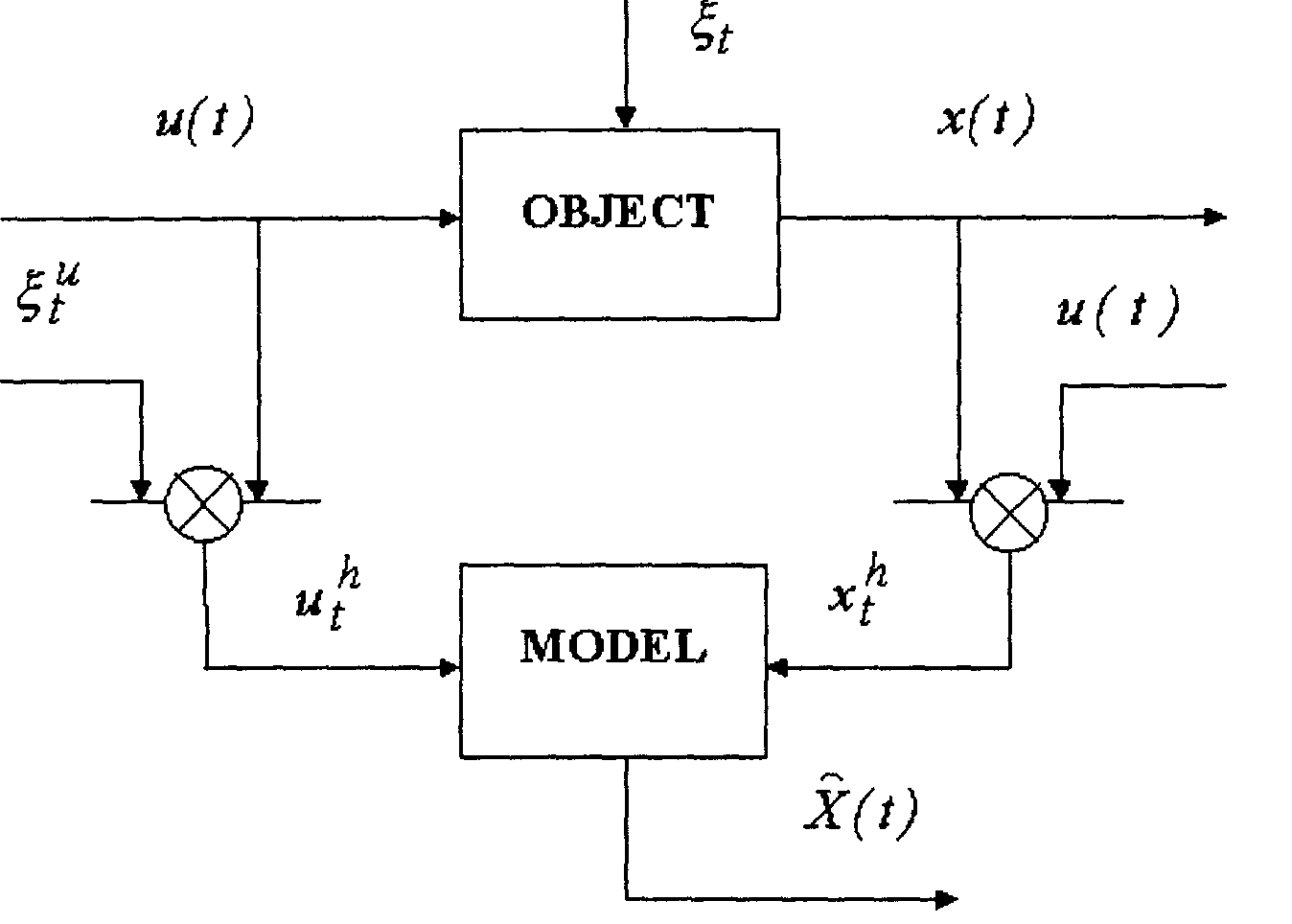
Fig.l. Identification problem statement.
its discrete analog:
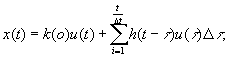 (2)
(2)
where k(t) and h(t) are transition and unit impulse response functions of the system respectively. Non-parametrical estimation of x(t) (non-parametrical model of LDS) will be sample [2]
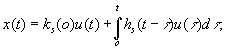 (3)
(3)
where ![]() , t = 0
and hs(t) are transition and unit impulse response functions of the
system respectively. Due to superposition principle this kind of model can be easily
generalized for the case, when n-dimensional vector u(t) is applied as the process
input. Than nonparametrical model of the process will have the following form:
, t = 0
and hs(t) are transition and unit impulse response functions of the
system respectively. Due to superposition principle this kind of model can be easily
generalized for the case, when n-dimensional vector u(t) is applied as the process
input. Than nonparametrical model of the process will have the following form:
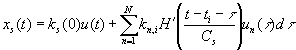 , (4)
, (4)
Numerical testing ofnon-parametrical models was performed. As objects for modeling differential equations of 2nd and 7th order were taken. Output of the model describing 2nd order object is represented at Fig.2. Input signal was taken as follows
u(t) =0.001t2+0.1t -1.
t
Fig.2. Response of the object (Хob) and model (Хm) to the input signal
u(t) = 0.001t2 + 0. 1t -1, data set size
s = 150; random noise ![]() = 5%.
= 5%.
Modeling of the 7th order dynamic object was also fulfilled. Results
are shown below at Fig.3. Input signal was taken as follows u(t) = log![]() +5
+5

Fig.3. Response of the object (Хob) and model (Хm) to the input signal
u(t) = log![]() + 5, data
set size s = 350, random noise
+ 5, data
set size s = 350, random noise ![]() =
5%.
=
5%.
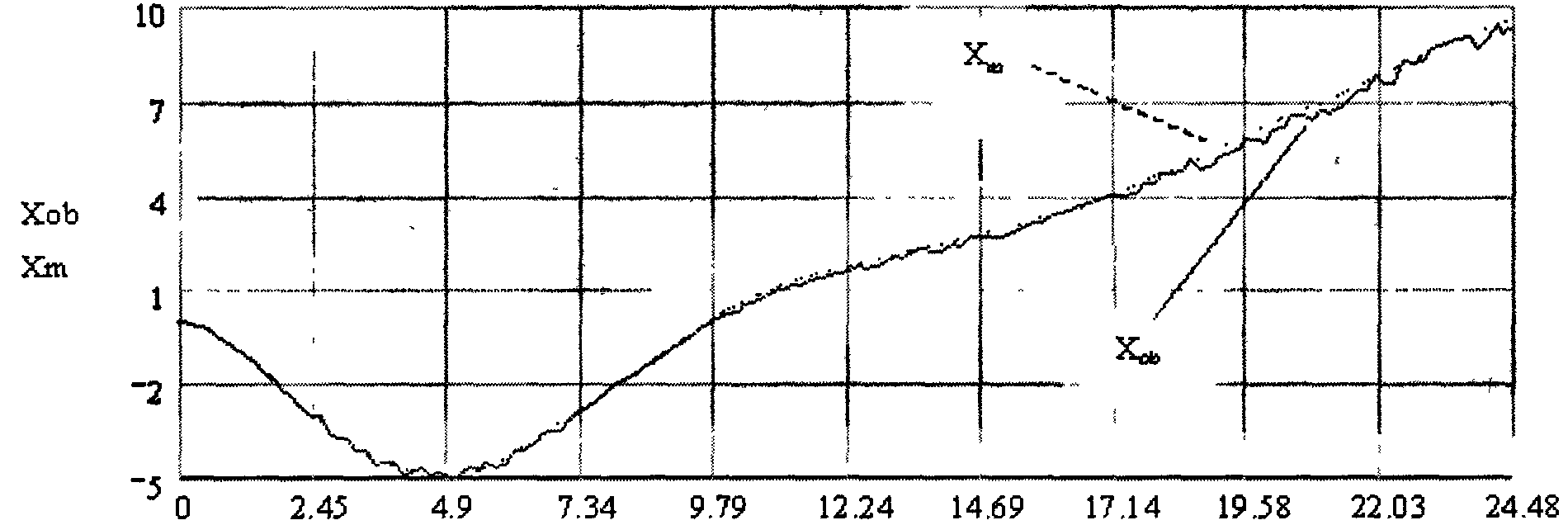
Results of multidimensional model operation are represented below. As parts of object, two dynamical units of 2nd and 3rd order were taken (Fig.4).
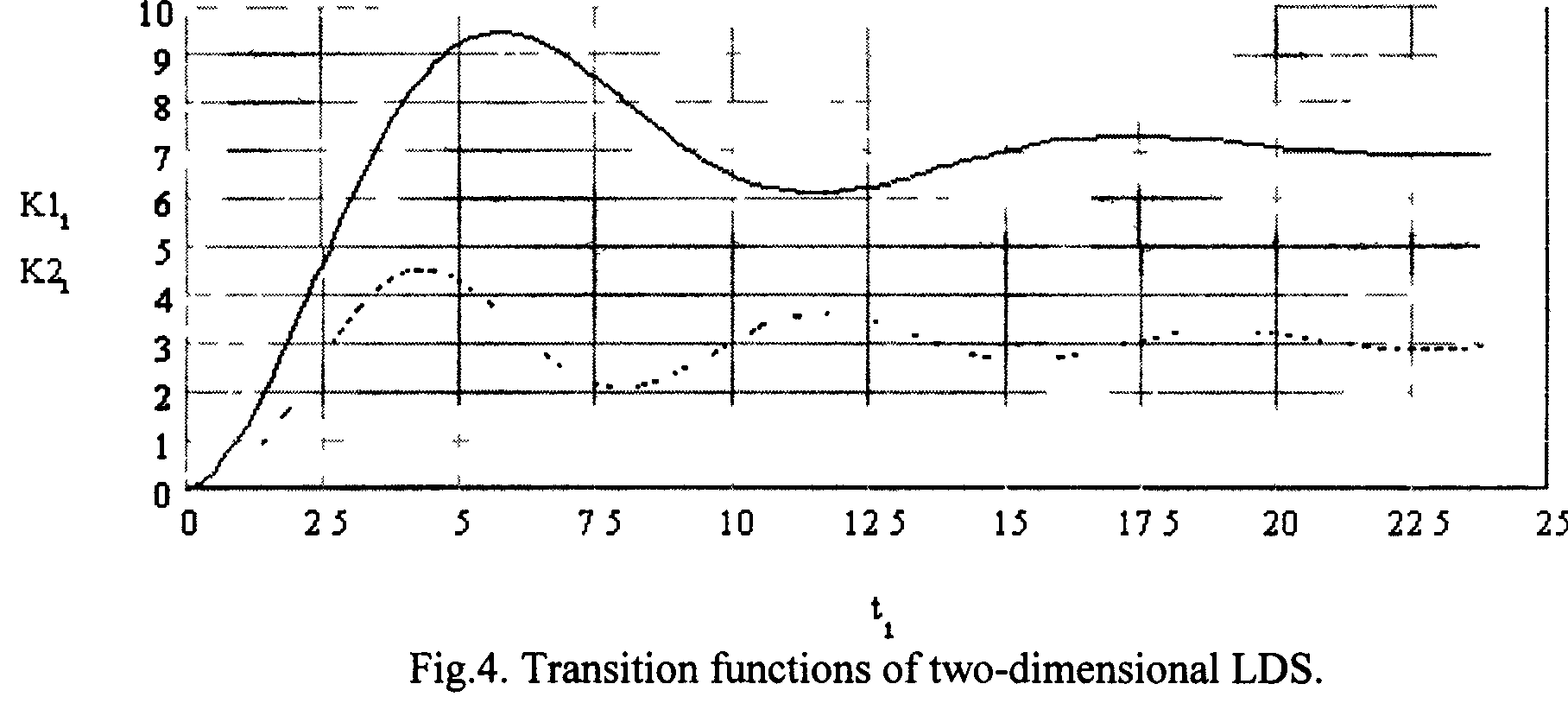
Fig.5 illustrates operation of multidimensional model. Input function of the first part:
![]()
Non-parametrical models have a number of advantages if compared to parametrical ones. They don't demand knowledge of an object structure. The method proved its ability during numerous experiments and tests.
References:
1. Medvedev A.V. Identification and Control For Linear Dynamic Systems for Unknown Order.// Optimisation Techniques IFIP Technical Conference/ Berlin - Heidelberg-New-York: Springer Verlag, 1975. - P. 48-55.
2. Medvedeva N.A. Nonparametrical Estimation of Statistical Characteristics in Problems of Modeling. Computer Data Analysis and Modeling. - Minsk: BSU, 1995, P. 89-93.
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|