Russia, Saint-Petersburg. Saint-Petersburg State Technical University

The choice problem of optimal parameters values for control systems of complicated technical objects is considered. Automated intellectual procedure is suggested for solving this problem. The procedure is based on sequential quadratic programming approach and realized in interactive conditions. It works successfully for ill-posed problems.

zim@ics2.ecd.spbstu.ru

Рассматривается задача выбора оптимальных значений параметров систем управления большими техническими объектами. Для ее решения предлагается автоматизированная интеллектуальная процедура, построенная на базе последовательного квадратичного программирования. Она реализована в интерактивном режиме и работает в условиях некорректной постановки задач.

Complicated technical systems have been acquired new dynamic properties in process of their development and increasing of elements number. These properties pose new control problems. On the one hand, the optimal parameters values selection problem becomes complicated by the inconsistency of control. It means that roots of characteristic equation are moved in opposite directions on a complex plane when parameters of control are being changed. On the other hand, this problem becomes complicated by the very long working time for one goal function evaluation in models of high dimension.

The problem of damping properties increasing in the neighborhood of stationary point is reduced to effective selection of the vector k of control system parameters in linearized model

(1)

where A - the system state matrix.

The search of the greatest stability degree defined by the real part of the right characteristic root is one of the ways to solve this problem. The principal disadvantages of this way are nondifferentiability of the goal function and the absence of all system dynamic properties consideration.

(2)

was considered. This function is oriented to the left shift on a complex plane for the group of eigenvalues of state matrix (1); are real parts of eigenvalues taken with inverse sign, - the fixed value of desired damping, v - the method parameter (v =2,3,4...).

Minimization of goal function F allows to improve a location of dominated eigenvalues group even for a case when the most right characteristic root is poorly controlled or couldn't be controlled at all. Function F may be generalized for a case of optimal choice of vector k components, which are common for a whole set of other model parameters (different from k).

Possible nonuniqueness of the solution for goal function optimization problem connected with the selection of parameter value may be avoided. A value of this parameter should be corrected in the process of numerical search during an accumulation of results. For the last steps of optimization process it may be selected close to the stability degree. Thus the intellectual procedure of sequential corrections of requirements to the control quality is suggested. These requirements are being changed according to the process of an accumulation our knowledge about the system.

Given procedure allows to automate a process of control parameters values selection for models of complicated technical objects. But this approach has a lack connected with very expensive evaluations of the goal function F. It means that each goal function evaluation requires full eigenproblem solving by QR-algorithm for the state matrix of (1). A working time of evaluations for models of complicated systems increases irresistibly.

The method described below is free of these lacks. Like as the optimized function is approximated by its quadratic model for sequential quadratic programming (SQP) methods, the linear model approximating the initial problem

, (3)

is built for each iteration of developed method. There is a vector describing increments of real parts of interested eigenvalues group, - a vector describing increments of parameters which are changed according to the optimization process, D is a sensitivity matrix with elements evaluated by widely known formulae

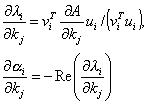, where (4)

A - the system state matrix, - its eigenvalues, and - eigenvectors of matrices A and A^T .

But immediate solution of the problem (3) leads to restrictions on characteristic roots moving on the complex plane through desired level of damping. That's why the additional vector p is introduced. This vector permits unconstrained shift to the left for dominated group of characteristic roots. Thus, the problem of quadratic programming

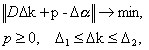(5)

is solved in one iteration. Constraints on are caused on the one hand by technical conditions for parameters' changing range and on the other hand - by the size of area where our quadratic model is valid.

The main working time of the method is connected with matrix D evaluation based on formulae (4) (the QR-algorithm is used) when model (3) is built. When problem (5) is being solved the working time is less, because the vector dimension isn't great (not all eigenvalues are considered) and the vector consists of parameters participating in control only.

Numerical experiments for given below areas were made for an effectiveness estimation of the suggested method. First research area was related to the selection of effective method for quadratic problem (5) solution. The following algorithms were compared:

• algorithm GPCG ( Gradient Projection Conjugate Gradient), which follows a strategy suggested by J.More in [3];

• algorithm BVLS (Bound Value Least Squares) suggested by C.L.Lawson and RJ.Hanson in [1];

• algorithm QPROG (Quadratic Programming) realizing the method described in the paper [4];

• algorithm QP (Quadratic Programming) included in numerical software MatLaM.2 andMatLab5.1.

The core of all algorithms solving quadratic programming problem is how many parameters included in the "active set" (all parameters which have been gone out on constraints on previous steps of algorithm are included in "active set") could be changed on the next step. For algorithms BVLS, QPROG, QP the changing is permitted for only one parameter with defined properties [2]. It was proved theoretically that if an attempt to change more than one parameter was done, then numerical procedure couldn't be continued in common case. The heuristic strategy to exclude several parameters from "active set" was realized in algorithm GPCG.

Numerical experiments for all algorithms proved the comparable effectiveness for the most part of applied problems. Moreover, the effectiveness of the algorithm GPCG in some cases was lower. This fact confirmed the necessity of strict justification for the intellectual strategy where the exclusion more than one parameter from "active set" during one iteration is suggested.

The analysis of different algorithms of trust region size selection defined by parameters and in (5) was the second research area. All considered algorithms are realized as heuristic strategies with the same quality behavior and differ one from another only by numerical coefficients [5,6]. The authors of these algorithms suggest comparable intellectual strategies where the evaluation of trust region size for the next step is based on the information received during the previous steps. Numerical experiments have shown that all strategies are comparable, but it is not possible to prefer one algorithm to another for all problems from different applied areas.

The last research area was the ill-posed case of the problem (5) solution. The solution with minimal norm represents the greatest interest, because it raises the confidence to quadratic model for the given iteration. In accordance with this point two-stage procedure has been developed. After receiving from (5) the second stage of the solving is defined as

(6)

Thus, the solution with minimal norm is selected. Moreover, it is very useful to relax the inequality . It allows to decrease the norm of vector and the necessary number of iterations for initial nonlinear problem solving.

Mechanics and power systems stability problems were used for the analysis of developed method. Test mechanical system with two inertial and one elastic elements was considered. The problem was to synthesize the regulator providing a desirable quality of the system for all set of the control parameters. The results of tests for different methods are represented in the table 1. These results are averaged by different start points.

Table 1. Numerical effectiveness of different methods.

FMINS - simplex-method.

FMINU - quasi-Newton method, used BFGS approximation of Hessian.

CONSTR - standard SQP-method.

NEW - developed SQP-method.

The testing was done by using numerical software Matlab5.1. The first three methods

represent standard software incapsulated in MatLab.

The goal function (2) was minimized by methods FMINS, FMINU and CONSTR. There were a lot of start points which were "bad" for these methods. It means that optimal solution couldn't be received. But the developed method allows to solve problems from all start points. It has been achieved:

• by developed interactive procedure supporting the decision whether the current step is successful or not;

• by using the intellectual strategy for trust region radius evaluation.

• by an attraction of additional information from applied area (such as mechanics, power systems, etc...).

Analogous results were received for the problem of the choice of optimal parameters values of power systems stabilizers (PSS) for large interconnected power systems [8]. Two test schemes were analyzed. The first was "New England" and the second represented some fragment of the Russian's power system.

Thus, the intellectual procedure of the choice of optimal parameters values for control systems of complicated technical objects is developed. It is based on sequential quadratic programming and may be used for the ill-posed problems. Quadratic programming algorithms are analyzed and compared in details. Two-stage procedure is suggested for ill-posed quadratic problems. This procedure allows to decrease the number of homer units for the initial nonlinear problem solving. The analysis of the different algorithms for the selection trust region radius has proved that the algorithm which would be optimal for different applied areas doesn't exist.

1. C.L.Lawson, RJ.Hanson Solving least squares problems //- M.: Nauka, 1986.-232 c.

2. P.E.Gill, W.Murray, M.H.Wright Practical optimization // - M.: Mir, 1985.-509 pp.

3. J.J. More , G.Toraldo Algorithm for bound constrained quadratic programming problems// Numer.Math.-1989.-43,N3, p.377-400.

4. Goldfarb, D., and A. Idnani A numerically stable dual method for solving strictly convex quadratic programs// Math. Programming.-1983.-27, p.1-33.

5. Branch M.A., Coleman T.F., Li Y. A subspace, interior and conjugate gradient method for large-scale bound constrained minimization problems, Comell theory center, CTC95- TR217, Cornell University, Ithaca, NY14583, USA.

6. Byrd R.H., Hribar M.E., Nocedal J. An interior-point algorithms for large-scale nonlinear programming, July 1997, TR, Rice University, Northwestern University, USA.

7. Wie В., Bernstein D. Benchmark Problems for robust control design // J.Of Guid., Contr., Dyn., V.15, №5,1992.

8. V.A.Maslennikov, S.M.Ustinov, and N.N.Shelukhin. The parameter optimization method for providing of bulk power system oscillatory steady-state stability// Energetika, Proc. of Russian Academy of Sciences, No 1, 1994, pp. 38-46.