Russia, Krasnoyarsk,

Research Institute For Control Systems, Wave Processes and Technologies,

Krasnoyarsk State Regional Power Station-2, Krasnoyarsk State Technical University,

e-mail: e_agafonov@yahoo.com

In the work one approach to cool burning processes mathematical modeling construction under non-parametrical uncertainty level is represented. The problems of the process quality control and optimization ave also described. Algorithms set of non-parametrical control and optimization, used in the approach, is the basis of algorithmical support system for boiler qualities control.

Россия, Красноярск,

Научно-исследовательский институт систем управления, волновых процессов и технологий, Красноярский Государственный Технический Университет, Красноярская государственная региональная электростанция 2,

e-mail: e_agafonov@yahoo.com

В работе рассматривается подход к построению математических моделей процессов горения угля в котлоагрегате в условиях непараметрической неопределенности, а также задача управления качеством процесса и его оптимизации. Используемые непараметрические алгоритмы моделирования, управления и оптимизации позволяют по мере поступления текущей информации об исследуемом процессе составить основу алгоритмического обеспечения системы управления качеством котлоагрегата.

При широком развитии информационных технологий в настоящее время по-прежнему остается открытым вопрос о моделирование технологических процессов дискретно-непрерывного характера в обстановке случайных факторов и различного рода неопределенностей действующих на них. Дискретно-непрерывные процессы доминируют в металлургии, нефтехимии, стройиндустрии и других отраслях. В частности, к дискретно-непрерывным процессам на тепловых электростанциях (ТЭС) могут быть отнесены: мельницы размола угля, паровые котлы, паровые турбины и др. Требования к режиму работы этих агрегатов достаточно высоки. Важным является также тот факт, что технологические процессы ТЭС подвержены действию случайных факторов и учет их в соответствующих системах моделирования и управления совершенно необходим. Естественно, что для моделирования и регулирования на объектах ТЭС необходимы современные методы теории стохастических и обучающихся систем.

Более подробно рассмотрим такой объект электростанции как котлоагрегат типа ПК-14-2. Основным процессом, протекающим в котле, является процесс горения. Данный котлоагрегат работает на твердом топливе, в пылевидном состояние. Процесс приготовления пыли сочетается с сушкой топлива. Сушка осуществляется одновременно с размолом в мельницах. При сжигании бурых углей в системе пылеприготовления с молотковыми мельницами угольная пыль, пройдя сепарационную шахту, вдувается через амбразуру в топку. Топка для сжигания топлива в пылевидном состояние представляет собой большую камеру, стены которой заполнены экранными трубами. Необходимый для горения воздух (первичный) вводится в топку вместе с пылью через горелки. Для полного сжигания пыли через завихрители выполнен подвод горячего воздуха. Вторичный воздух способствует перемещению и быстрому сгоранию аэросмеси [1].

Для того чтобы котлоагрегат эффективно работал в условиях нормальной эксплуатации необходимо выполнять следующие правила:

• работа топки котла должна корректироваться согласно, нагрузок котла так, чтобы обеспечить постоянное и нормальное давление пара;
• при нормальном горении факел должен иметь светложелтый (соломенный) цвет и равномерно заполнять топочное пространство;
• при регулировании процесса горения в топке не допускать резких изменений процесса, пульсации факела и т.д. путем регулирования подачи воздуха;
• не допускать отклонение О₂ от нормы больше, чем на 0.5%.

Регулирование топочного процесса осуществляется следующим образом:

• все работающие шахтные мельницы нагружаются, по возможности, одинаково, что дает равномерную загрузку топочной камеры;
• регулировку факела производят таким образом, чтобы внизу он был выше холодной воронки, не лизал заднюю стенку топки и не поднимался выше определенной отметки.

В настоящее время основным способом корректировки протекания топочного процесса, является визуальное наблюдение за процессом горения. Основываясь данными наблюдениями, лицо принимающее решение производит, в соответствии с правилами нормальной эксплуатации, необходимые корректировочные действия.

Использование информационных технологий моделирования дают возможность, при хорошо развитом алгоритмическом и программном обеспечении, исследователю, технологу, ЛПР, используя соответствующие модели, проводить исследования интересующих их процессов и объектов. Подобная схема представлена на рисунке 1.

Входными воздействиями являются следующие параметры: температура аэросмеси, температура воздуха, температура питательной воды, расход топлива, расход воздуха, расход питательной воды, химический состав питательной воды, влажность топлива, тонина помола, качество топлива.

Выходными параметрами является: температура острого пара, давление острого пара, расход острого пара, содержание О₂ в уходящих газах, температура уходящих газов.

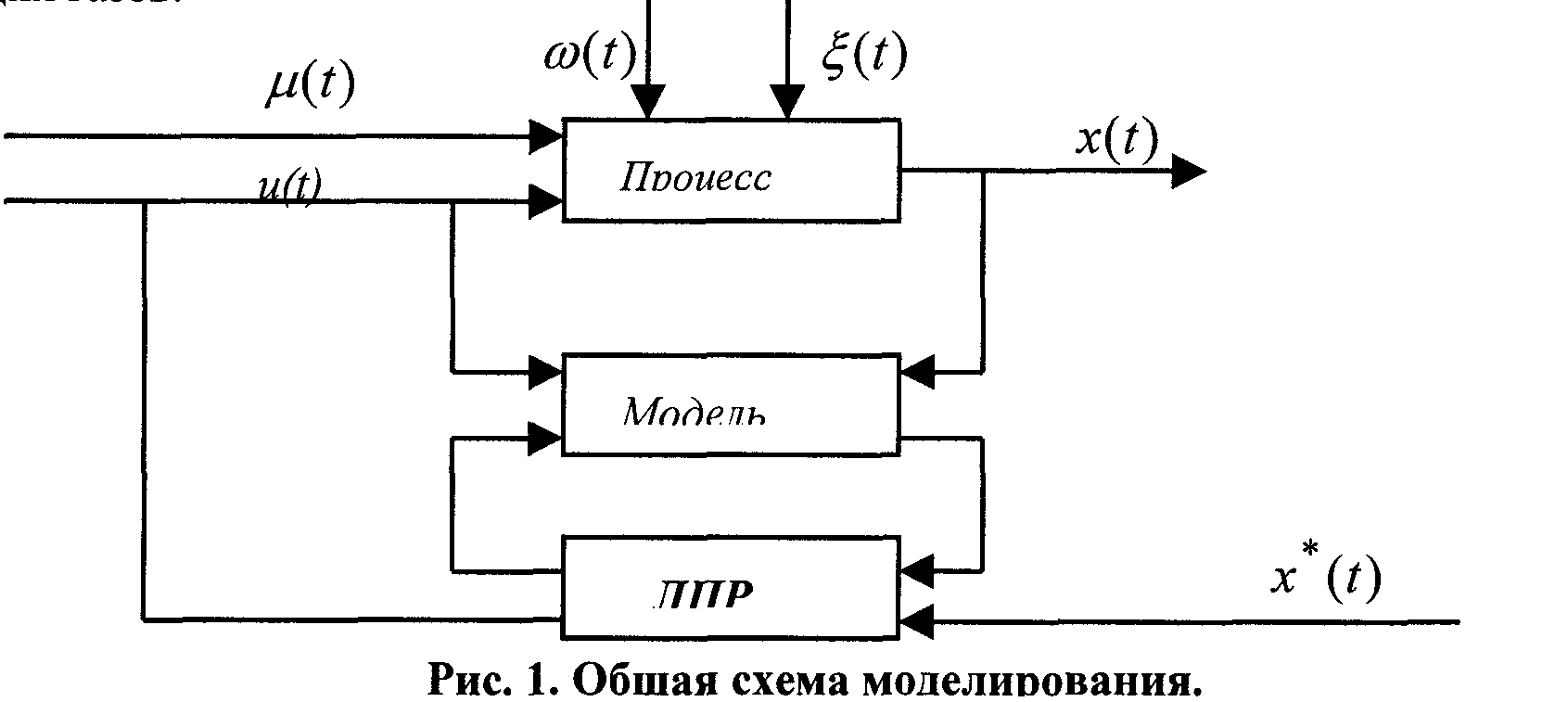
На рисунке приняты обозначения: — вектор выходных переменных процесса, которые без нарушения общности, можем считать скалярными, и — соответственно управляемые и неуправляемые контролируемые переменные, — не контролируемые переменные, действующие на процесс (а ее существование исследователь может и не знать), — случайные возмущения, t — время. Таким образом, — может быть представлена в виде объективно существующей зависимости:

(1)

где А — неизвестный оператор процесса, , , , .

Измерение векторов переменных , и осуществляется со случайными ошибками, имеющими нулевое математическое ожидание и ограниченную дисперсию, плотность вероятности их неизвестна. Обозначим эти наблюдения , , , , здесь t — дискретное время.

Для формулировки той или иной задачи необходима информация об операторе А, цели управления, случайных помехах, действующих на объект, ограничениях. Нами для алгоритмизации процесса использовалась теория непараметрических систем.

Для решения задачи моделирования процесса горения угля в котлоагрегате будем использовать непараметрический алгоритм идентификации объектов без памяти, которые имеют вид:

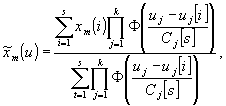(2)

Рассмотрим задачу управления процессом в условиях непараметрической неопределенности. Введем некоторую функцию качества , — заданное значение выхода процесса в момент времени t. Сформулируем критерий оптимальности:

(3)

где — решающая функция.

Оптимальный оператор, определяющий , равен:

, (4)

Поскольку для показателя качества , который представляет собой меру уклонения от , естественно потребовать равенство нулю, тогда (4) перепишется в виде:

, (5)

Теперь задача сводится к непараметрическому оцениванию (5) на основании поступающей информации , . В качестве непараметрической оценки (5) может быть принята статистика[2]:

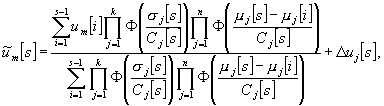(6)

где , , а , j — количество входных управляемых переменных.

Рассмотрим случай, когда выбор управления подчинен ограничениям вида:

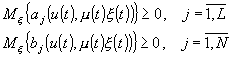(7)

Выпишем критерий оптимальности:

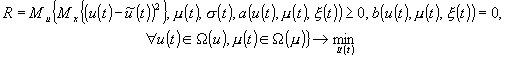(8)

Непараметрическая оценка имеет вид:

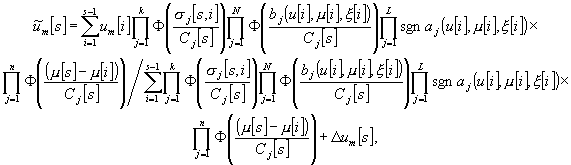(9)

где для произвольного аргумента z:

Приведенные алгоритмы предполагают последовательную схему обучения. Задача управления котлоагрегатом — согласовать потоки подаваемых в котел питательной воды, топлива и воздуха, необходимые для обеспечения требуемой паропроизводительности котла при заданных параметрах пара.

На основе выше изложенного материала были разработано алгоритмическое обеспечение системы управления качеством работы котлоагрегата на Красноярской ГРЭС 2.

Литература

1. Рыжкин В.Я. Тепловые электрические станции.//. Москва-Ленинград. Издательство “Энергия”. 1967 г. 400с.
2. Медведев А.В. Адаптация в условиях непараметрической неопределенности -В кн.: Адаптивные системы и их приложения. Новосибирск, “Наука” Сибирское отделение, 1978 4-33 с.