Russia, St.-Petersburg, Naval Academy

Abstract. The new results of development of a common logical-probabilistic method for automatic construction of analytical, statistical, Markov and network mathematical models of systems of arbitrary structure are set up.

Россия, Санкт-Петербург, Военно-Морская Академия

ВЕРОЯТНОСТНЫХ МОДЕЛЕЙ СИСТЕМ

Реферат. Излагаются новые результаты развития общего логико-вероятностного метода для автоматического построения аналитических, статистических, марковских и сетевых математических моделей систем произвольной структуры.

Общий логико-вероятностный метод (ОЛВМ) включает в себя следующие четыре этапа [1,2]: 1) постановка задачи моделирования путем построения специальной структурной схемы функциональной целостности (СФЦ): 2) определение логической функции работоспособности системы (ФРС); 3) построение многочлена расчетной вероятностной функции (ВФ); 4) вычисление вероятностных показателей системы. Современная теория и технология автоматизированного ОЛВМ [3-б][основывается на ручной структурной постановке задачи моделирования, путем построения СФЦ исследуемой системы. Все последующие этапы определения расчетных математических моделей (логической и вероятностной) выполняются автоматически с помощью ЭВМ. Для этого разработаны специальные программные комплексы автоматизированного структурно-логического моделирования (ПК АСМ) [7].

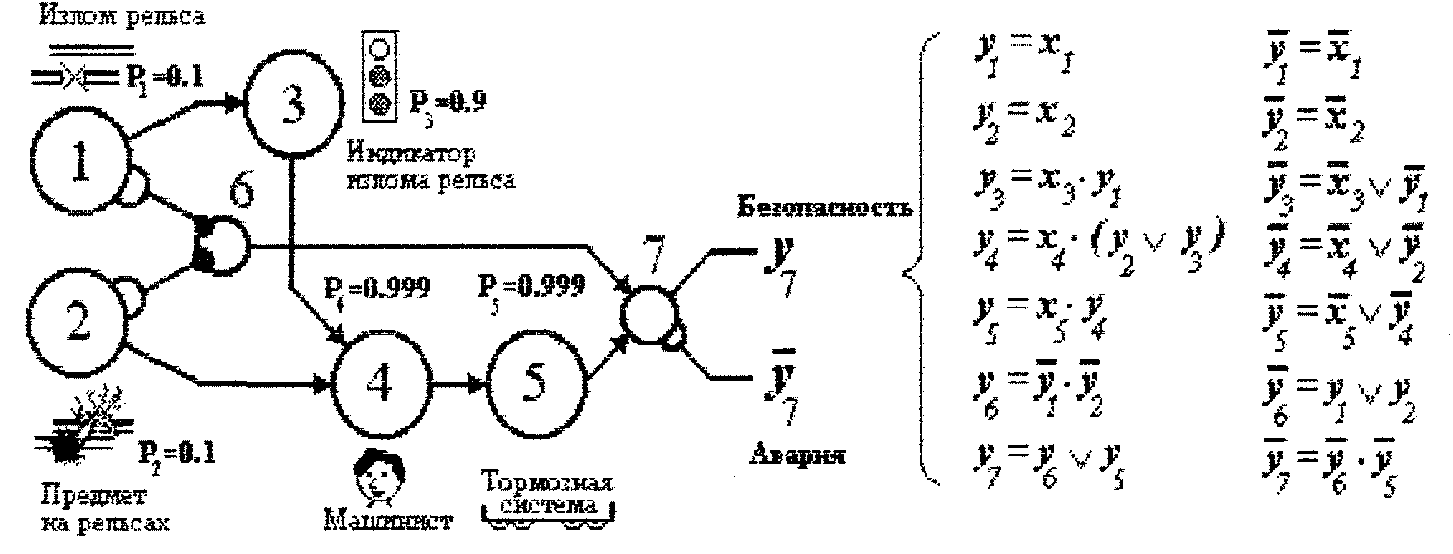
Технологию автоматизированного ОЛВМ проиллюстрируем простым примером построения математических моделей безопасности, аварии и риска гипотетического участка железной дороги (ж.д.). СФЦ системы приведена на рис. 1.

Она состоит из пяти логически связанных бинарных событий: - излом рельса, - предмет на рельсах; - безотказная работа индикатора излома рельса; - своевременное включение машинистом тормозной системы поезда; - безотказность тормозной системы. Подробное описание постановки и ручного решения данной задачи приведено в [4]. Здесь мы остановимся на технологических аспекты использования ОЛВМ для автоматического построения нескольких видов математических моделей систем, структуры которых могут быть представлены с помощью аппарата схем функциональной целостности.

Технология автоматизированного аналитического ОЛВМ предусматривает ввод в ЭВМ СФЦ системы, вероятностных параметров ее элементов и логического критерия исследуемого режима ее функционирования. В примере критерием безопасности является выходная функция . Далее, с помощью ПК АСМ [7], автоматически формируются логическая ФРС и многочлен расчетной вероятностной функции безопасности:

(1)

(2)

С помощью ОЛВМ можно автоматически получать логические и вероятностные модели большой размерности, до нескольких сотен и тысяч слагаемых. В отличие от классических монотонных ЛВМ, общий логико-вероятностный метод реализует функционально полный набор операций алгебры логики "И", "ИЛИ", "НЕ". Это позволяет автоматически строить как все виды монотонных, так и новый класс - немонотонные аналитические модели систем произвольной структуры. В настоящее время в автоматизированном ОЛВМ реализованы следующие новые возможности моделирования.

Учет в вероятностной модели системы различных законов распределения вероятностей ее элементов (экспоненциальный, нормальный, Вейбулла-Гнеденко и др.).

1. Расчет показателей роли отдельных элементов в определении общесистемной вероятностной характеристики:

- значимость

- положительный вклад

-отрицательный вклад

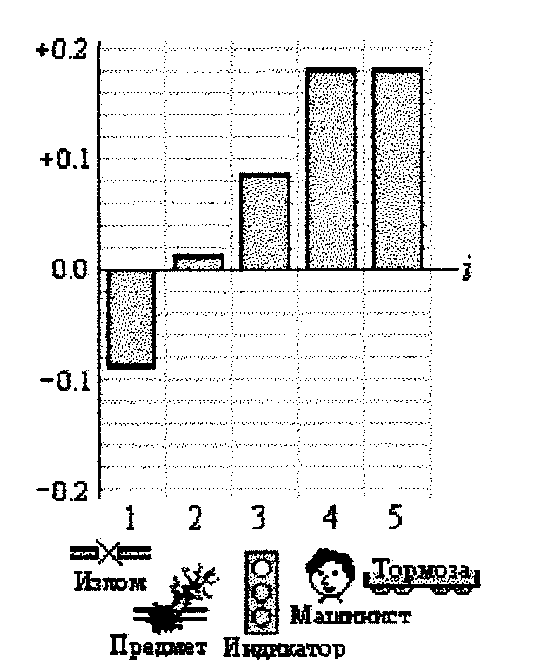
На рис. 2 приведены графики значимости элементов в обеспечение безопасности рассматриваемого участка ж.д.

2. Учет групп несовместных (зависимых) событий (ГНС) и множественных (больше двух) собственных состояний элементов системы. Он основывается на нескольких специальных (новых) законах алгебры логики и правилах вычисления вероятностей: Если , то:

Так, если допустить в рассматриваемом примере, что исходные события и несовместные (), то вероятностная модели безопасности (2) изменится:

Учет ГНС позволил существенно повысить качество моделирования и расширить область применения технологии автоматизированного аналитического ОЛВМ.

Технология автоматизированного статистического ОЛВМ предусматривает ввод в ЭВМ тех же исходных данных (СФЦ, параметров элементов и ЛКФ), однако далее, с помощью ПК АСМ [7], автоматически формируется имитационная (статистическая) модель исследуемой системы. В настоящее время реализованы два подхода к автоматизации процессов логико-вероятностного построения статистических моделей систем. Первый подход основывается на так называемом логико-статистическом методе (ЛСМ) академика И. А. Рябинина. В ЛСМ и ОЛВМ первые два этапа совпадают. В результате формируется явная аналитическая форм логический ФРС (например (1)). Далее она рассматривается как основа, для организации проведения машинных статистических испытаний и получения оценок вероятностных показателей исследуемой системы. Таким образом, в ЛСМ исключена необходимость автоматического построения (иногда очень громоздких!) многочленов расчетных ВФ. Второй подход основывается на так называемом итерационном логико-статистическом методе (ИЛСМ), разработанным доцентом А.О.Алексеевым [3]. В ИЛСМ исключена необходимость явного построения на ЭВМ всех аналитических моделей - и многочленов ВФ и логических ФРС. Получение оценок вероятностных характеристик систем в ИЛСМ основывается на специальных машинных процедурах статистического решения любых (монотонных и немонотонных) систем логических уравнений, задаваемых СФЦ (см. например рис. 1), и расчета значимости всех элементов. Так, с помощью ИЛСМ реализованного в [7], были получены результаты статистического вероятностного анализа безопасности участка ж.д., , , , , . Эти результаты согласуются с аналитическими решениями задачи (см. (2) и рис.2).

Технология автоматизированного ОЛВМ построения марковских моделей систем первоначально была разработана для расчета условных законов живучести систем к воздействию на их элементы различных последовательностей поражающих факторов [2]. Был автоматизирован самый громоздкий и трудоемкий процесс построения, на основе СФЦ и ЛКФ, самой цепи Маркова, т.е. графа переходов состояний системы и всех допустимых переходов. В ОЛВМ множество марковских состояний работоспособности системы определяется путем автоматического преобразования логической ФРС в совершенную дизъюнктивную нормальную форму (СДНФ). Затем, на основе специальных правил поразрядного сравнения пар конъюнкций полученной СДНФ автоматически определяются допустимые логические функции переходов (ЛФП) между марковскими состояниями системы и рассчитываются их параметры. Например, правила поразрядного сравнения переменных конъюнкций СДНФ логической ФРС для определения переменных ЛПФ между состояниями цепи Маркова для невосстанавливаемых систем, следующие:

Если , то - не поражение элемента ;

Если , то - поражение элемента ; (4)

Если , то - элемент уже поражен;

Если , то - элемент не восстанавливается,

Построенная по указанным правилам марковская цепь системы, СФЦ которой приведена на рис. 1, характеризуется 13-ю комбинаторными марковскими состояниями безопасности и 70-ю допустимыми переходами между этими состояниями. Правила, аналогичные (4), и соответствующие машинные программы разработаны для нескольких видов поражающих воздействий, систем с ГНС и восстановлением элементов. Технология ОЛВМ построения цепей Маркова позволяет полностью автоматизировать процессы построение практически всех известных видов и классов дискретных и непрерывных марковских и полумарковских моделей систем большой размерности, состояния которых описываются конъюнкциями простых логических переменных.

Технология автоматизированного ОЛВМ построения моделей реальной эффективности. Способность ОЛВМ строить немонотонные модели устойчивости (надежности, живучести и безопасности) впервые позволила объединить эти модели с множеством других, специальных моделей, характеризующих условную эффективность функционирования систем в различных состояниях [2,5] .

(5)

Здесь М- количество областей состояний в которых система функционирует с разной эффективностью , a - вероятность нахождения системы в этих состояниях 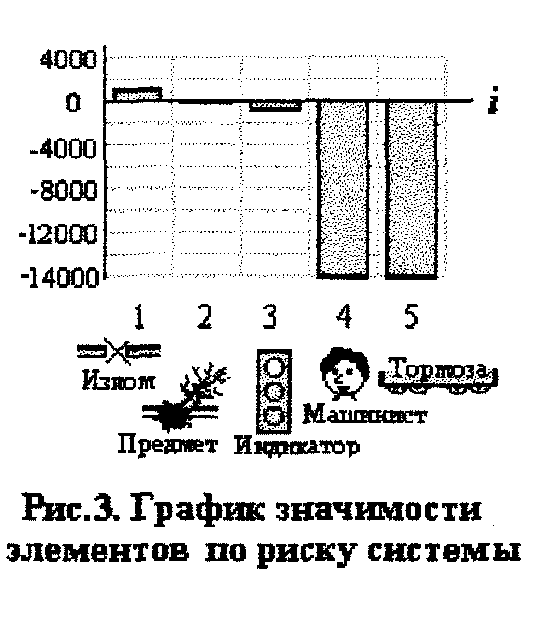(определяется автоматически ПК АСМ). Тогда - математическое ожидание эффективности системы с учетом ее устойчивости.

Оценим с помощью (4) риск аварии на рассматриваемом в примере участке ж.д. Для этого допустим, что авария по причинам одновременного возникновения излома рельса и предмета на рельсах оценивается в 15000 ye. последующих затрат, авария только из-за излома рельса - 10000 ye., а только из-за предмета на рельсах - 5000 ye. Тогда, реальный риск затрат вследствие аварии на участке ж.д. можно автоматически оценить, с помощью ПК АСМ по критерию

у.е.

Технология автоматизированного ОЛВМ анализа сетевых систем предусматривает построение математических моделей таких объектов, в структуре которых должны учитываться не только комбинации, но и последовательности элементарных событий во времени. Такие комбинаторно-последовательные модели могут использоваться при решении задач учета ненадежности переключающих устройств, при поиске на множестве решений, синтезе сетевые планы и др. Для автоматизации процессов построения последовательных моделей функционирования систем потребовалась разработка специальных правил построения и записи функций алгебры логики. Комбинаторно-последовательной является, например, ФРС (1). Представляет интерес противоположная комбинаторно-последовательная логическая модель аварии участка ж.д. [6]:

Функция (6) формируется автоматически и представляет все возможные минимальные комбинации и последовательности событий, приводящие к ж.д. аварии. Это позволяет использовать технологию автоматизированного ОЛВМ не только для вероятностного анализа безопасности, но и для управления безопасностью в реальном масштабе времени функционирования системы.