 |
||
Flegontov A.V.
Russia, St.-Petersburg,
Institute for Informatics and Automation of the Russian Academy of Science
E-mail: afleg@spiiras.nw.ru
AUTOGENERATION OF NONLINEAR DYNAMICS MODELESS
Abstract. Consider general approach to the building of differential complex of nonlinear models and forecasting algorithm, based on solution the inverse problems of symmetry analysis — a building of models with the a priori symmetry. Cite an instance polynomial multivariable models and singular structures in the forms of special functions.
Флегонтов A.B.
Россия, Санкт-Петербург, Институт информатики и автоматизации РАН,
E-mail: afleg@spiiras.nw.ru
АВТОГЕНЕРАЦИЯ НЕЛИНЕЙНЫХ ДИНАМИЧЕСКИХ МОДЕЛЕЙ
Аннотация. Рассматривается общий подход к построению дифференциального комплекса нелинейных моделей и прогнозирующий алгоритм, основанные на решении обратных задач симметрийного анализа — построении моделей с априорной симметрией. Приводятся примеры полиномиальных многопараметрических моделей и сингулярные структуры в виде специальных функций.
Мощность множества возможных типов дифференциальных операторов больше мощности множества континуума.
Н.Н. Моисеев, “Алгоритмы развития”
Современный этап развития математического моделирования характеризуется стремлением к максимальной регулярности разрабатываемых алгоритмов и процедур с использованием фундаментальных свойств динамических систем, в частности, симметрий и законов сохранения. К настоящему моменту получили распространение и широко внедряются прогнозирующие алгоритмы, основанные на решении обратных задач симметрийного анализа — построении моделей с априорной симметрией.
Порождаемые модели естественным образом отражают изучаемые процессы и явления с помощью введенных формализмов. Динамические минимальные модели (в трактовке Н.Н. Моисеева) описываются, как правило, одним из векторных дифференциальных уравнений
![]() (1)
(1)
где
у — т-мерный фазовый вектор,Формирование таких моделей существенным образом опирается на симметрийный и структурный анализ и синтез, т.к. знание симметрии уравнений (1) приводит к применению групповых операторов и всему многообразию методов современной теории групп Ли-Беклунда. Возникающие, при этом, генераторы групп преобразований (особенно дискретных) и порождают семейства соизмеримых подобных динамических моделей. А структурное подобие, в свою очередь, позволяет выделить класс структурно-устойчивых моделей в виде определенного D - комплекса.
Для заданных многообразий ![]() ,
, ![]() , оператора полного дифференцирования D
и оператора дискретной симметрии
, оператора полного дифференцирования D
и оператора дискретной симметрии ![]() (генератора группы) определим D
-комплекс в виде
(генератора группы) определим D
-комплекс в виде
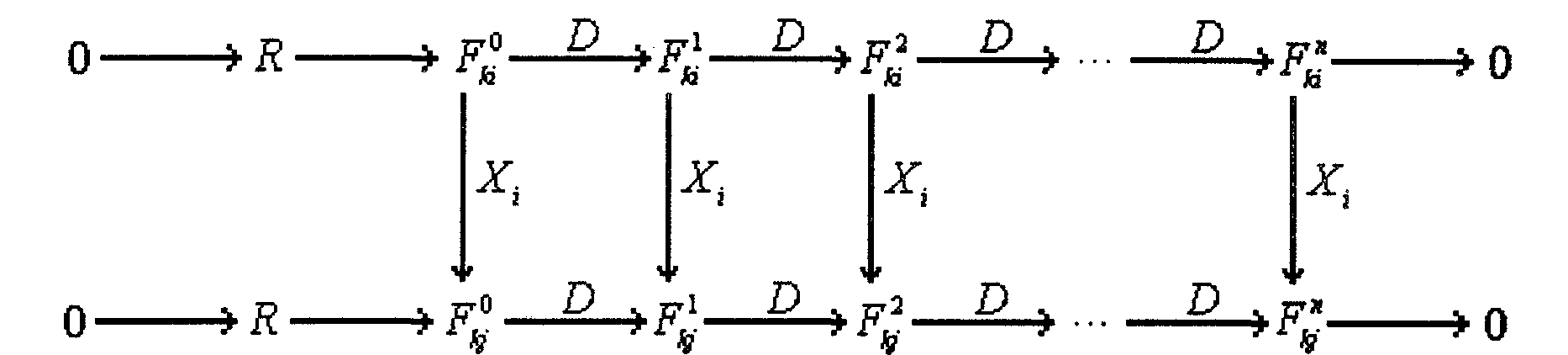
В общем случае введенный комплекс
определяет для ![]()
Последовательное применение операторов полного дифференцирования и симметрии для задач синтеза динамических моделей [3] приводит к следующему алгоритму автогенерации (общий случай):
1. [Представление]. Задание структуры интегрального многообразия над дифференциальным полем алгебраических функций, причем для явной формы достаточно одно образующее соотношений, а для параметрической — два.
2. [Дифференцирование]. Применение оператора полного дифференцирования D к многообразию по независимой переменной или по параметру.
3. [Нормализация]. Исключение произвольных констант. Если задана параметрическая форма представления, то необходимо обратить ее относительно параметра и затем исключить его из системы. Приведение к нормальному виду.
4. [D-генерация]. Построение дифференциальных продолжений и формирование моделей в соответствии с шагами 2 и 3.
5. [![]() -генерация].
Применение генераторов групп
-генерация].
Применение генераторов групп ![]() к полученным моделям и формирование
классов подобных моделей.
к полученным моделям и формирование
классов подобных моделей.
Выполнение шага 4 сохраняет все априорные симметрии для получаемых моделей и порождает новые продолженные для каждого k-продолжения. На 5-ом шаге изменяется структура интегральных многообразий получаемых моделей, порожденная на шаге 1 и определяемая тем же полем.
Пример 1. Пусть структура
интегрального многообразия при ![]() и произвольном
и произвольном ![]() имеет вид:
имеет вид:
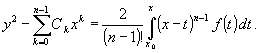 (2)
(2)
Используя соотношение
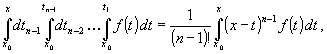
и, применяя цепочку D-генерирующих
отображений, получим последовательность моделей
вида (1) над интегральными многообразиями ![]() , структура которых
порождается одним и тем же базисным
многообразием (2)
, структура которых
порождается одним и тем же базисным
многообразием (2)
![]() (3)
(3)
![]() (4)
(4)
В уравнениях (3) - (4) коэффициенты
функций ![]() согласованны
с константами интегрального многообразия (2), a
согласованны
с константами интегрального многообразия (2), a ![]() — произвольная
функция.
— произвольная
функция.
Т.о., получаем как 4-х параметрический класс дифференциальных уравнений 1-го порядка вида (3), допускающий 4-х параметрическое семейство общих решений в виде (2) с функциональным произволом, так и уравнение 5-го порядка (4), разрешимого в виде (2) (уравнение 5.2.6.1 справочника [2]).
Приведенные в виде (3) - (4) модели легко обобщаются на случай произвольного n с заданной структурой (2).
Рассмотрим некоторое семейство
моделей полиномиального типа, коэффициенты
которых являются полиномами относительно
зависимой и независимой переменных [2]. Такие
модели представляются в виде ![]() , где число свободных параметров в Р
и Q определяется структурой и
соответствующими параметрами интегрального
многообразия. Будем синтезировать такие модели
из голоморфного подмножества в параметрическом
виде
, где число свободных параметров в Р
и Q определяется структурой и
соответствующими параметрами интегрального
многообразия. Будем синтезировать такие модели
из голоморфного подмножества в параметрическом
виде ![]() ,
, ![]() , где
, где
![]()
Применение алгоритма автогенерации приводит к полиномиальным моделям, структура которых отражена в таблице 1.
Пример 2. Рассмотрим некоторые сингулярные структуры интегральных многообразий, к которым приводят особые значения вектора параметров дискретных групп преобразований подкласса обобщенных уравнений Эмдена-Фаулера [1]. Пусть исходная структура интегрального многообразия имеет вид:
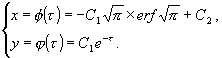 (5)
(5)
Цепочка D -отображений приводит последовательно к уравнениям
![]() (6)
(6)
а при дополнении (5) константами ![]() и выполнении условий гладкости, и к
и выполнении условий гладкости, и к
![]() (7)
(7)
Таблица 1.
№ |
|
|
|
|
1а |
2 |
|
|
|
1b |
2 |
|
|
|
2 |
2 |
|
|
|
3 |
|
|
|
|
4 |
3 |
|
|
|
5 |
4 |
|
|
|
С учетом композиций преобразований сингулярных орбит, в частности вида
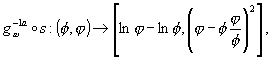 (8)
(8)
получим остальные элементы D-комплекса.
Так, например, для новых переменных ![]() , первое из уравнений (6) перейдет в (9)
, первое из уравнений (6) перейдет в (9)
![]() (9)
(9)
ОУЭФ (второе в (6)) и (7) преобразуются в соответствующие уравнения
![]()
Аналогичными структурами обладают и подклассы уравнений, решения которых выражаются через функции Бесселя и ряд других интегральных выражений.
ЛИТЕРАТУРА
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|