Russia, Moscow, Reacont-Ltd Company, reacont-ltd@mtu-net.ru

The report presented is devoted to the synthesis of the specified field in the bounded region for laboratory-scale plant realization. In general case, this problem is reduced to the linear equations system calculation. As this one is ill-posed, minimal norm method [2] is proposed for the task solution. Besides, special arrangement of the sources is considered. Such arrangement allows to solute the problem by means of DFT method.

Россия, Москва, ЗАО НТП “Реаконт”, reacont-ltd@mtu-net.ru

Представленный доклад посвящен описанию синтеза заданного поля в ограниченной области в лабораторных условиях. В общем случае, эта задача сводится к решению системы линейных уравнений. Поскольку данная система является плохо обусловленной, предлагается метод минимальной нормы [2] для ее решения. Помимо этого, рассматривается особое расположение источников, позволяющее решить задачу с помощью ДПФ.

Во многих отраслях современной науки и техники часто требуется синтезировать в заданной ограниченной области (или на поверхности) поле с определенным амплитудно-фазовым распределением. Это необходимо, например, при отработке приемных антенных систем в гидро- или радиолокации. В большинстве случаев, требуется имитировать поле, создаваемое достаточно удаленными источниками. Поля таких источников суть плоские волны, поэтому задачу можно свести к проблеме синтеза одной плоской волны пришедшей с заданного направления.

Настоящая работа посвящена рассмотрению практически реализуемых алгоритмов алгоритмов, позволяющих решить поставленную задачу в лабораторных условиях.

2.Синтез поля на конечном числе узлов.

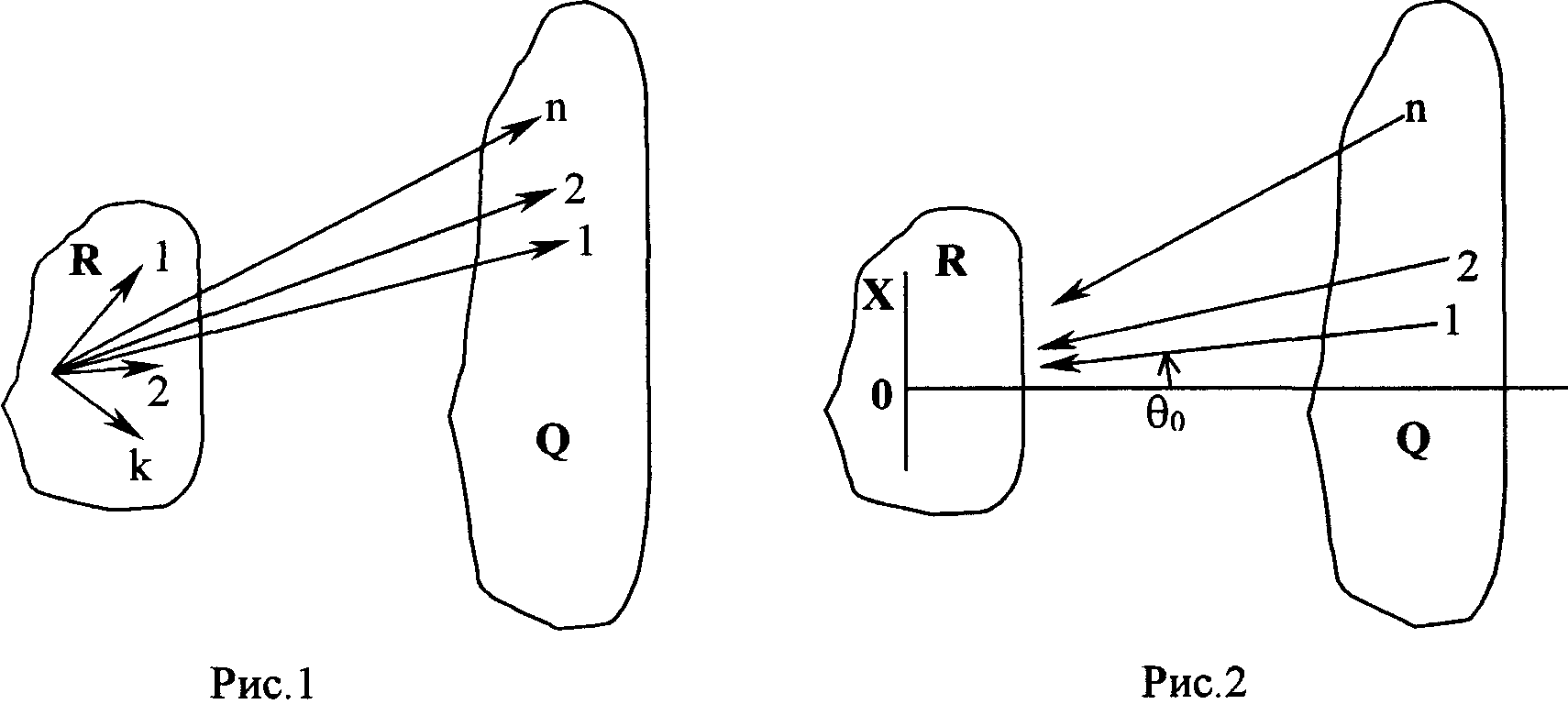
Пусть в некоторой среде (см. Рис.1) с помощью N излучающих точечных элементов необходимо получить в на М узлах, расположенных в области R , поле S_m. Если положение точечных элементов, излучающих поле U_n , в области Q определяется радиус-векторами , а положение узлов — радиус-векторами , то поле в узловых точках можно представить как

(1)

Это соотношение можно представить в матричном виде

S = E? U (2)

где — столбец узловых сигналов;

— столбец сигналов источников;

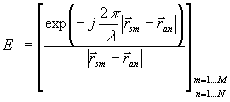— матрица преобразования

Матричное уравнение (2) можно рассматривать как систему линейных уравнений относительно неизвестных U_n . Если М=N, то при det(E)? 0 существует точное и однозначное решение системы (2):

U = E^-1? S (3)

Если число узлов моделирования меньше числа источников (М<N), то существует множество решений системы (2) (требуемое поле можно создать многими способами). В случае, когда M>N (переопределенная система), существует приближенное решение которое можно найти, например, методом наименьших квадратов:

U = (E^+? E)^-1? E^+? S (4)

3. Синтез поля в ограниченной области

Для того чтобы иметь практическую ценность, полученное точное или приближенное решение должно быть устойчиво как по отношению к положению источников и узлов, так и по отношению к излучаемым сигналам. Другими словами, поле моделирования не только на узлах, но и между ними должно мало отличаться от требуемого. Для этого матрицы Е в выражении (3) или E^+? E в выражении (4) должны быть хорошо обусловлены. Это можно рассматривать, как особое требование к расположению как приемных, так и излучающих узлов. Если, например, приемные узлы в области R удалены друг от друга не более чем на l /2, то в случае, когда требуется синтезировать поле S(r) c ограниченным пространственным спектром, то по теореме Котельникова[1] задания поля на таких узлах S_m=S(r_sm) достаточно для решения задачи во всей области R. Погрешность синтеза будет тем ниже, чем больше угловой размер области Q.

Относительная амплитудная погрешность

Если, кроме того, число узлов моделирования M меньше числа источников N (неоднозначность решения), то можно существенно снизить погрешность интерполяции между узлами используя метод минимальной нормы [2], обычно применяемый для решения некорректно поставленных задач.

В этих условиях решение можно определить с помощью псевдообратной матрицы Ep:

U = Ep^-1? S (5)

Ep^-1 = (E^+? E)^-1? E⁺ (6)

При этом в узловых точках получается исходное поле, а в произвольной точке области R поле будет определяться следующим соотношением:

(7)

Соотношение (7) можно переписать с учетом (5) в виде

S’(r) = E’(r)? Ep^-1? S (8)

где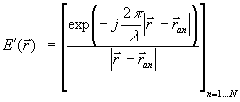

Соотношение (8) представляет, таким образом, матричную форму интерполяционной формулы, которая связывает значение поля в дискретных узлах интерполяции и значение поля в произвольной точке области R.

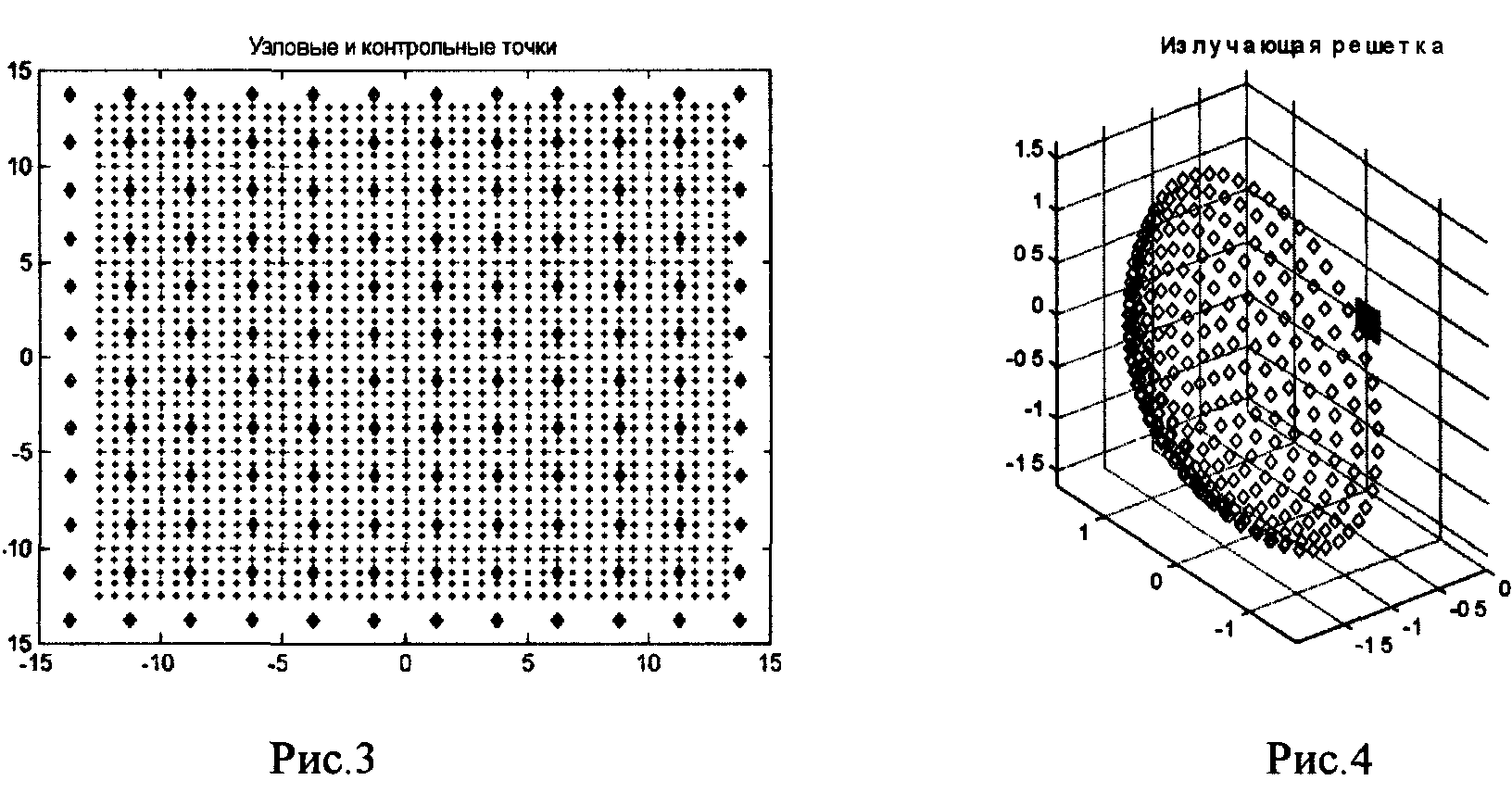
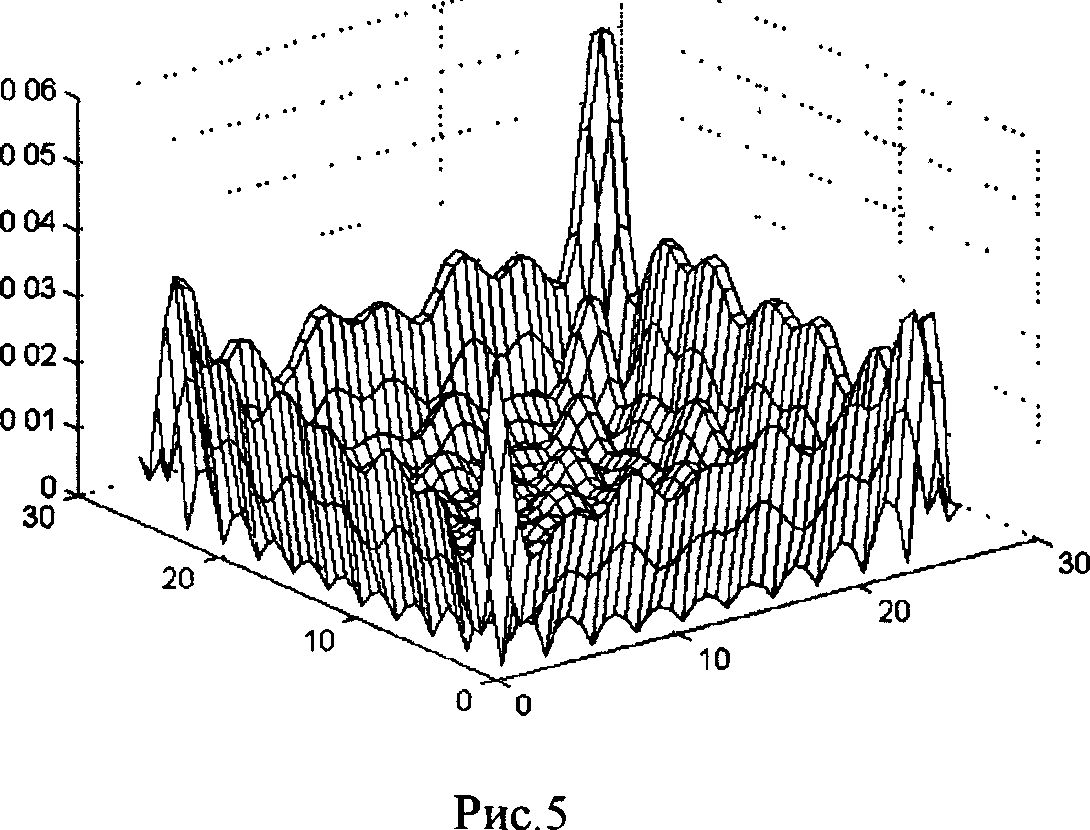
В качестве примера использования такого метода ниже приводятся результаты имитационного моделирования. На Рис.3 показаны расположенные на плоскости узловые точки интерполяции. Их число равно 12? 12=144. Расстояние между узловыми точками составляет половину длины волны (l = 6 см). Кроме того, на этом же рисунке показаны более плотно расположенные контрольные точки, число которых равно 42? 42=1764. Размер плоской области интерполяции равен 27? 27 см. На Рис.4 показано расположение элементов излучающий решетки. Они равномерно заполняют часть сферической поверхности радиусом 2 м с телесным углом 120° . Число излучающих элементов равно 312. Область интерполяции расположена в центре сферы. Имитировалось поле точечного источника в дальней зоне с угловыми координатами: азимут 20° , угол места 20° . На Рис.5 показано распределение относительной погрешности интерполяции плоского фронта источника. Как видно из рисунка, в центральной области погрешность сравнительно мала (около 0.01); по краям области погрешность возрастает( до 0.06).

4. Синтез модельного поля с помощью дискретного преобразования Фурье.

При значительном числе излучающих источников практическая реализация алгоритма минимальной нормы (особенно в задачах реального времени) может быть затруднена. С другой стороны, можно выбрать такое расположение источников, которое может значительно снизить требуемый объем вычислительных затрат.

Рассмотрим двумерную задачу (см. Рис.2). Пусть источники расположены далеко от узлов и n-й источник виден из области Q под углом J _n = arcsin[n? sin(J ₀)]. Тогда поле S(x) вдоль прямой OX в области R имеет вид

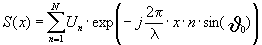(9)

Легко видеть, что задача синтеза требуемого поля сводится к задаче вычисления коэффициентов Фурье функции S(x). Если поле задать на эквидистантных узлах, то массив сигналов источников U_n находится c помощью обратного дискретного преобразования Фурье. Хорошо проработанные алгоритмы быстрого преобразования Фурье позволяют эффективно решить поставленную задачу в реальном времени.

Литература

1. Левин Б.Р. Теоретические основы статистической радиотехники. Т.2, М., 1968

2. Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. М, 1986