Russia, Krasnoyarsk,

Research Institute For Control Systems, Wave Processes and Technologies,

Krasnoyarsk State Regional Power Station-2, Institute of Computing Modeling,

Krasnoyarsk State Technical University,

e-mail: e_agafonov@yahoo .corn

On the report problems of identification and control of the power unit local circuits are represented. The problem of technical condition diagnosis of technological devices and equipment of coal power station also takes place. The basis of algorithmical support of computer control and diagnosis system is the set of non - parametrical algorithms.

Россия, Красноярск,

Научно-исследовательский институт систем управления, волновых процессов и технологий. Красноярская государственная региональная электростанция 2, Институт вычислительного моделирования. Красноярский государственный технический университет,

e-mail: e_agafonov@yahoo. com

В докладе рассматриваются задачи идентификации и управления локальными контурами энергоблока. Так же рассматривается задача диагностики технического состояния технологических установок и оборудования ТЭС. Основу алгоритмического обеспечения разрабатываемой компьютерной системы управления и диагностики составляют непараметрические алгоритмы.

В последнее время в промышленности широкое применение получили информационные технологии моделирования и управления технологическими объектами, которые увеличивают скорость обработки информации, позволяют более эффективно осуществлять управление технологическими процессами. Это ведет к росту уровня автоматизации компьютеризации управления для дискретно непрерывных процессов. Такие процессы доминируют в металлургии, нефтехимии, стройиндустрии, а также в теплоэнергетике и других отраслях.

Ключевым звеном тепловой электростанции (ТЭС) является энергоблок. Который, в свою очередь представляет собой достаточно сложный многоконтурный объект управления и может быть разбит на более простые составляющие компоненты: котел, турбинный парогенератор и др. Данные объекты охвачены контурами автоматического регулирования. На пятом энергоблоке Красноярской ГРЭС-2 установлены шестнадцать типов регуляторов, которые выполнены на аппаратуре серий РПИБ-III, РПИБ-Т, РПИВ-М. Данные устройства являются регуляторами по отклонению и используют стандартные ПИ, ПИД законы регулирования.

Настройка регуляторов производится по переходным (разгонным) характеристикам объектов. На рисунке 1 показана переходная характеристика котла, входом которого является угль, подающийся в топку котла, а выход - давление пара за котлом.

Для построения эффективно действующих локальных систем управления объектами необходимо решение задачи идентификации. Наиболее широко распространенной в настоящее время является задача идентификации в “узком” смысле, то есть когда последняя разбивается на два этапа: первый - состоит в выборе класса модели с точностью до параметров, а второй - последующей оценки этих параметров по наблюдениям ошибки процесса “входа - выхода”. Наименее разработанной является теория идентификации в “широком” смысле, содержание которой состоит в том, что класс параметрических моделей не может быть определен из-за недостатка априорных сведений, но известен класс операторов, описывающих исследуемый процесс.

Суть предлагаемого подхода к решению задачи идентификации рассматриваемого класса объектов изложена в [1]. Непараметрическая модель линейной динамической системы (ЛДС) в дискретном виде выглядит следующим образом:

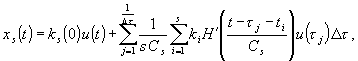(1)

где — оценка переходной характеристики, — входное воздействие, —параметр размытости, — колоколообразная функция, — дискретность интегрирования, — переменная интегрирования, и удовлетворяют условиям сходимости.

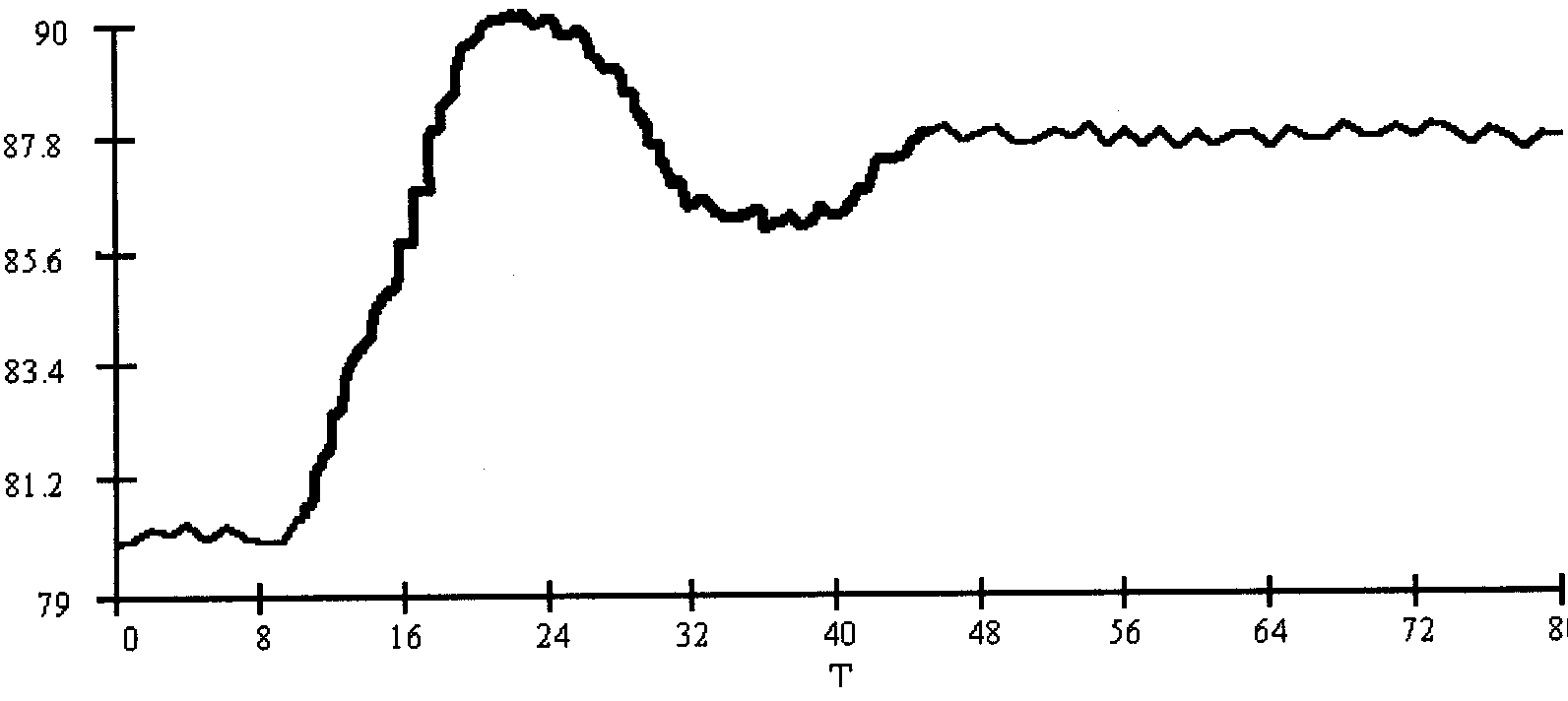
Рис. 1. Разгонная характеристика котла по давлению пара (кг/см ).

Во многих случаях технологические процессы (объекты) могут быть отнесены к классу линейных. На практике для регулирования подобными процессами используется П-, ПИ-законы регулирования и др. Ясно, что широко используемые законы регулирования являются далеко не лучшими.

Изложим подход к синтезу регулятора [2]. Известно, что обратный оператор ЛДС имеет тот же вид, что и прямой оператор ЛДС, с той лишь разницей, что весовая и переходная функции определяются в направлении “выход-вход”. Поскольку на реальном объекте такие реализации получить нельзя, “обратные” характеристики (характеристики снимаемые в направлении “выход-вход”) “снимаются” с модели ЛДС, решая уравнение . Решение данного уравнения — есть алгоритм для отыскания реализации “обратной” переходной функции и выглядит следующим образом:

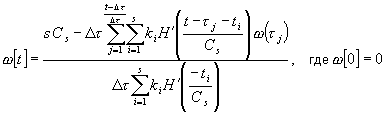(2)

Полученная реализация используется для построения “обратного” оператора ЛДС, оценка которого приведена ниже:

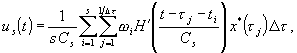
где — оценка “обратного” оператора, — реализация “обратной” переходной, — задающее воздействие, функция и параметр размытости удовлетворяют условиям сходимости.

При обследовании энергоблока №5 Красноярской ГРЭС-2 было зафиксировано 85 контрольных точек, которые можно отнести к температурному, химическому контролю, контролю давления и уровня в различных технологических установках и оборудовании. Контрольные точки можно также разделить на две группы: характеризующие качество технологического процесса (температура и давление острого пара, содержание кислорода в уходящих газах и т.д.) и характеризующие техническое состояние оборудования (температура металла турбины, котла, температура подшипников, содержание водорода в охладительной системе и т.д.). По данным точкам можно судить о качестве технологического процесса и техническому состоянию оборудования. В связи с тем, что оборудование подвержено воздействию различных факторов, таких как износу, эрозии, разрушению рабочих поверхностей, старению, то возникает задача диагностики оборудования.

Эти задачи можно свести к решению задач распознавания образов (РО) и использовать соответствующий математический аппарат. Традиционно задача РО состоит в отнесении предъявляемого объекта к одному из классов. Классы характеризуются тем, что принадлежащие им объекты обладают некоторым сходством. Если существует возможность обозначить общее, что объединяет объекты в классы, в виде векторов признаков, то в общем виде задача сводится к сравнению предъявляемых для опознавания объектов с заранее известными, т.е. элементами обучающей выборки — , где — вектор значений признаков, — "указания учителя" о принадлежности элемента к одному из классов. Этот процесс называют обучением с учителем. Для этого строится некоторая разделяющая поверхность (решающая функция ) и решающее правило, в соответствии с которым по знаку принимается решение о принадлежности предъявляемого для экзамена объекта к тому или иному классу [3], [4]. В вероятностной постановке задачи РО обычно существует одна наилучшая разделяющая поверхность в смысле минимума выбранного критерия оптимальности.

В рамках второго подхода вероятностные характеристики классов заменяются их непараметрическими оценками. Большой популярностью пользуются оценки плотности ядерного типа, введенные Розенблатом и Парзеном [5]. Положив, что элементы платежной матрицы равны нулю при , сходящаяся к байесовой непараметрическая оценка решающей функции в двуальтернативной задаче примет вид

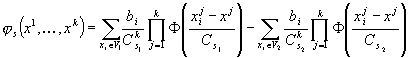(4)

где 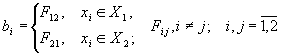— потери при отнесении ситуации из класса i к классу j ; где — вектора признаков элементы — обучающей выборки —1; , — элементы, принадлежащие классу , , — элементы, принадлежащие классу ; — финитная колоколообразная интегрируемая с квадратом функция и параметры размытости , удовлетворяют некоторым условиям.

Знак оценки (4) позволяет различать рассматриваемые области (классы), решающее правило можно сформулировать по аналогии с байесовым [4]:

(5)

Алгоритм оптимизируется по параметрам размытости в ходе скользящего экзамена. Критерием выбора в качестве оптимального является минимальное количество ошибок во время скользящего экзамена на обучающей выборке.

Задачу диагностики оборудования и режимов протекания технологических процессов можно интерпретировать как двуальтернативную задачу распознавания образов. Где состояние исследуемого объекта, описываемое набором характеристик, следует относить к первому классу, если оно соответствует регламентируемому режиму, ко второму классу - если характеристики выходят за рамки заранее предписанного регламента.

Литература

1. Медведева Н.А. Непараметрические модели и регуляторы // Известия Вузов. Физика. Томск 1995. № 9. С. 124-129.
2. Кузнецова О.В. Медведева Н.А. Пупков А.Н. Об исследовании непараметрического регулятора. // Перспективные материалы, технологии, конструкции: Сб. науч. тр. / Под ред. проф. В.В. Стацуры. - Вып. 4. -Красноярск: САА, 1998. - С. 346-351.
3. Медведев А.В. Непараметрические системы адаптации. Новосибирск: Наука, 1983,174с.
4. Цыпкин Я.З. Основы теории обучающихся систем. Москва: Наука, 1970, 251с.
5. Parzen Е. On estimation of probability density function and mode. //Ann. Math. Stat., 1962, Vol.33, P.1065-1076.