 |
||
Rurua A.A., Sesadze V.K., Kekenadze V.M., Gugushvili A.Sh.
Georgia, Tbilisi.
Georgian Technical University.
Email: alik@ gtu.edu.ge
APPLICATION OF A TWO-STEP IDENTIFICATION ALGORITHM AND THE CATASTROPHE THEORY TO FORECAST RESTRICTED ZONES OF THE TECHNOLOGICAL PROCESS CONTROL
This article discusses questions of combined application of the two-step identification algorithm with the methods of the catastrophe theory makes it possible to forecast unstable areas of control, to make necessary corrections of the impact of control and to avoid intrusion into restricted control areas (of defective product manufacturing).
Руруа А. А., Сесадзе В.К., Кекенадзе В.М., Гугушвили А.Ш.
Грузия, Тбилиси
Грузинский технический университет
Email: alik@ gtu.edu.ge
ПРИМЕНЕНИЕ ДВУХШАГОВОГО АЛГОРИТМА ИДЕНТИФИКАЦИИ И ТЕОРИИ КАТАСТРОФ ДЛЯ ПРОГНОЗИРОВАНИЯ ЗАПРЕТНЫХ ЗОН УПРАВЛЕНИЯ ТЕХНОЛОГИЧЕСКИМИ ОБЪЕКТАМИ
В статье рассматриваются вопросы совместного применения двухшагового алгоритма идентификации и методов теории катастроф для прогнозирования неустойчивых областей управления, осуществления необходимой корректировки управляющего воздействия и исключение попадания в запретные зоны управления (выпуска бракованной продукции).
Adaptive methods are widely used for the creation of automated control systems for complex technological processes in order to improve the quality of the manufactured goods. This required introduction of adaptive control systems (ACS) with an identificator in the chain of reverse connection (ACS) [1].
The main element of the ACS is an identificator, the purpose of which is to create a mathematical model of the automated object and to forecast its output value. The purpose of identification with a given structure of the object is to evaluate the parameters of the model. Various identification algorithms have been developed in this direction.
In the ACS introduced at Pervouralsk, Dnepropetrovsk and Rustavi steelworks a single-step identification algorithm -"Kachmazha" has been used [1].
Perfection and latest developments of computer technology used in ACS enable us to utilize more complex but improved parameters of identification algorithm.
Recently, considerable attention has been paid to the development of multi-step algorithms having much better characteristics in comparison with the single-step algorithms.
The present paper considers the issues in connection with the utilization of two-step algorithm in order to extend the ACS functions. As the ACS provides improvement of the qualitative data of the system. (Considerable decrease of the controlled value dispersion) we face a problem to considerably decrease production of defective goods.
In this regard, methods of catastrophe theory are proposed to be used together with the identification algorithm. As is well known, the methods of disaster theory enable us to determine unstable zones of the object (catastrophe zones) which correspond to the emergency situations.
Combined application of the two-step identification algorithm with the methods of the catastrophe theory makes it possible to forecast unstable areas of control, to make necessary corrections of the impact of control and to avoid intrusion into restricted control areas (of defective product manufacturing).
TWO STEP IDENTIFICATION ALGORITHM FOR THE EVALUTION OF LINEAR OBJECT PARAMETERS
Multidimensional linear object comprising a wide class of technological procedures including the pipe-rolling processes has been considered:
![]() (1) Where -
(1) Where - ![]() is output of the object
is output of the object
![]() - Vector of the
parameters of the n dimension object
- Vector of the
parameters of the n dimension object
![]() - Transposition sign
- Transposition sign
![]() -Input vector of the
object, containing n-1 occasional disturbance
-Input vector of the
object, containing n-1 occasional disturbance
![]() -Controlling variable
-Controlling variable
N -discrete time N=1,2,3...
The identificator on the basis of input and output values makes a model of the object according to the equation
![]() (2)
(2)
Where ![]() - is
output;
- is
output; ![]() -vector of the parameter values of
the object at N -1 step.
-vector of the parameter values of
the object at N -1 step.
Parameters are evaluated by two-step algorithm, using the information of "input and output" on two phases of discrete time. Analitical output of the algorithm ireceived from the so called"basic allgorithm [2].
Let's mark N and N-1 time vectors of input of the object by ![]() and
and ![]() and corresponding outputs by
and corresponding outputs by ![]() and
and
![]() .
.
Model of the object this time will be described by the system of these equations
![]()
![]()
In these markings the two- step algorithm looks as
|
(3) |
Where ![]() is a parameter
of the algorithm
is a parameter
of the algorithm ![]() .
.
Evaluation of average input and output values around which the initial parameters are centered, centering and normalization is done by special algorithms [1]
Dispersion of variables is determined by these values - ![]() .
.
Output value ![]() is
defined by
is
defined by ![]() factor and measured input
values. By means of the discovered model of the object the control .impact is calculated.
Implementation of it guarantees equality of output value with the given value of
factor and measured input
values. By means of the discovered model of the object the control .impact is calculated.
Implementation of it guarantees equality of output value with the given value of ![]()
![]() (4)
(4)
All the identification procedures like determination of control impact and its implementation is carried out by the ACS. Average values of output and input as well as their dispersions calculated during the process of identification can be used as initial data to determine the disaster zones.
DETERMINATION OF RESTRICTED CONTROL ZONES BY THE METHOD OF THE DISASTER THEORY
Experiments on the majority of linear objects, namely on pipe rolling devices have shown that input values are distributed in accordance with the regular rule.
Curve of possibility distributions of the pipe-rolling device output
value of the pipe-wall thickness is given on fig.l. Curve 1 corresponds to the manual
control, while curve. 2 corresponds to the automated control, which is carried out by
means of ACS. ![]() and
and ![]() minimum and maximum values of the pipe wall,
according to the Soviet standards;
minimum and maximum values of the pipe wall,
according to the Soviet standards;
![]() - is a given value
of the wall thickness;
- is a given value
of the wall thickness; ![]() - new given
value.
- new given
value.
A and В zones are restricted areas or disaster zones in accordance with the terminology used in theory of disasters.
Control system should function so that values of the wall thickness should not exceed the limits, that means to meet strictly these conditions
![]() (5)
(5)
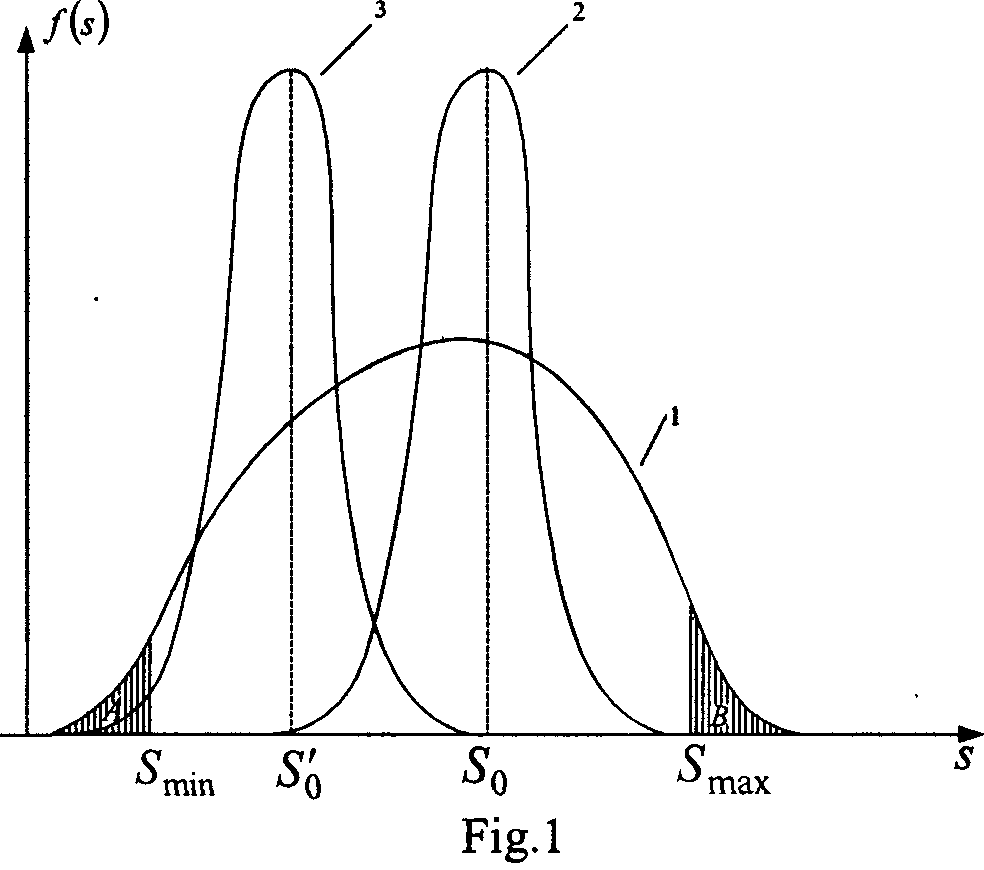
Application of ACS for controlling pipe-rolling device has decreased the dispersion of the average wall thickness of pipes by 35-40%[1]. Utilization of two step algorithm increases accuracy of forecast in comparison with one step algorithm; thus ACS provides more decrease of dispersion [4]. Decrease of this dispersion excludes violation of conditions; namely possibility of defect occurrence is almost zero.
Practically, in order to obtain greater effect, given value of ![]() is substituted by a new
is substituted by a new ![]() value that enables us to produce pipes in
the area of minus possibilities. Meanwhile curve 2 moves to the minimum possible values
(curve 3). This results in considerable increase of pipe- rolling effectiveness,
significant decrease of metal usage due to the decrease of the weight of each linear meter
of the pipe.
value that enables us to produce pipes in
the area of minus possibilities. Meanwhile curve 2 moves to the minimum possible values
(curve 3). This results in considerable increase of pipe- rolling effectiveness,
significant decrease of metal usage due to the decrease of the weight of each linear meter
of the pipe.
However the possibility of intrusion into A zone ![]() increases and the production of defect goods
is relatively higher, namely pipes with walls
increases and the production of defect goods
is relatively higher, namely pipes with walls ![]() thinner than limited.
thinner than limited.
In addition to this, in order to obtain greater effectiveness of the
ASC, zone ![]() can be attained to the
restricted zone in addition to the В area. Though the inrusion into this zone is not a
disaster and doesn't cause production defects, it is not economically reasonable.
can be attained to the
restricted zone in addition to the В area. Though the inrusion into this zone is not a
disaster and doesn't cause production defects, it is not economically reasonable.
Different methods can be used to avoid intrusions into the restricted control zones. However, for the objects ran by the ACS, using two-step identification algorithm together with the method of the catastrophe theory can solve problems of the intrusion forecast into the restricted zone.
R.Tom's theory of catastrophe is based on the investigation of the local behavior of the stationary distribution probability to which the system moves when . Stationary distribution can be viewed with a certain possible surface in the space with parameters and investigate this surface by means of the theory of catastrophe. Sharp changes in the shape of the surface correspond to the sharp qualitative changes in the behavior of the present system- catastrophe [5].
Probability of density distribution is determined as follows:
![]() (6) Where
(6) Where ![]() - is an output value,
- is an output value, ![]() and
and ![]() - are parameters dependent on the average value of
- are parameters dependent on the average value of ![]() dispersion.
dispersion.
This distribution achieves maximum at point у =0, which corresponds to the position of balanced equilibrium. It is known, that potential function is the reverse function of the distribution density, namely
![]() (7)
(7)
This equation, according to![]() . Tom, corresponds to the diaster of assembly type. Catastrophe occur, when
. Tom, corresponds to the diaster of assembly type. Catastrophe occur, when
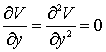 (8)
(8)
Using condition 8 in order to express (7) and exclude Y, we'll get
![]() (9)
(9)
Equation (9) gives semicubic parable, see fig.2.
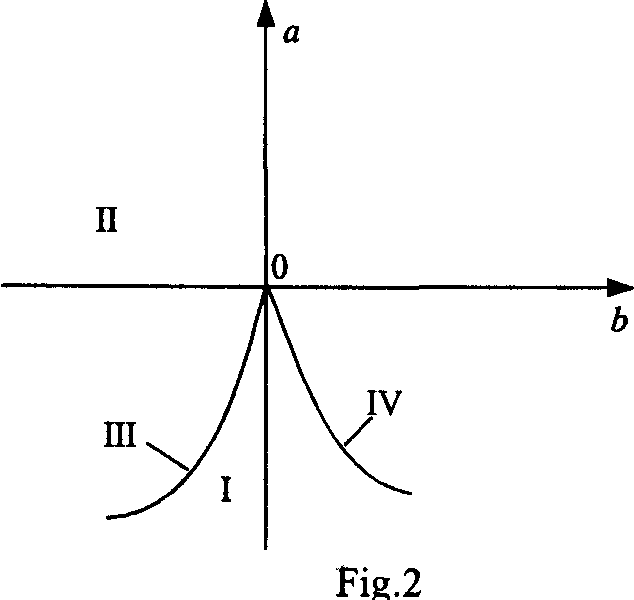
Equation (9) is a D-discriminate for
![]() (10)
(10)
![]() (11)
(11)
If ![]() , equation
(10) has three different substantial roots, when
, equation
(10) has three different substantial roots, when![]() , such root will be one, if
, such root will be one, if![]() , then multiple roots. That's why the equation (9) gives
, then multiple roots. That's why the equation (9) gives ![]() on the surface which is called bifurcation
curve. This curve breaks the surface of
on the surface which is called bifurcation
curve. This curve breaks the surface of ![]() parameter control into five regions (I, II, III, IV and point 0). Critical points are
located in the III and IV regions. That's why, if the parameters get into restricted zone,
it is necessary to correct
parameter control into five regions (I, II, III, IV and point 0). Critical points are
located in the III and IV regions. That's why, if the parameters get into restricted zone,
it is necessary to correct ![]() in order to
get out of the critical areas.
in order to
get out of the critical areas.
When![]() ,
, ![]() and
and ![]() parameters are on semicubic parable and are critical. When
parameters are on semicubic parable and are critical. When![]() ,
, ![]() and
and ![]() parameters get into
region I where the values of
parameters get into
region I where the values of ![]() and
and ![]() parameters are more or less acceptable.
parameters are more or less acceptable.
When![]() ,
, ![]() and
and ![]() parameters get into region II and values of the parameters from this region
give good results.
parameters get into region II and values of the parameters from this region
give good results.
![]() And
And ![]() factors are determined as follows:
factors are determined as follows:
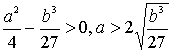 (12)
(12)
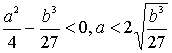 (13)
(13)
We can conclude that combined usage of two-step identification
algorithm and catastrophe theory makes it possible to form the conditions for correcting
control impact, namely, correction is done when ![]() and
and ![]() are in regions III
and IV. Correction is not required when
are in regions III
and IV. Correction is not required when ![]() and
and ![]() are in region II. As for the
region I and point 0, final decision is .made by the operator of the system.
are in region II. As for the
region I and point 0, final decision is .made by the operator of the system.
DETERMINATION OF THE CORRECTED CONTROL IMPACT
In order to avoid intrusion into the restricted control zone, it is necessary to correct control impact determined by equation (4).
Corrected control inpact is determined by equation
![]() (14)
(14)
Where ![]() -is correcting
factor, dependent on the parameters of
-is correcting
factor, dependent on the parameters of ![]() and
and ![]() potential function.
Implementation of the calculated control impact excludes probability of getting into
restricted zone, namely production of defective goods.
potential function.
Implementation of the calculated control impact excludes probability of getting into
restricted zone, namely production of defective goods.
Chart of corrected control impact algorithm implementation
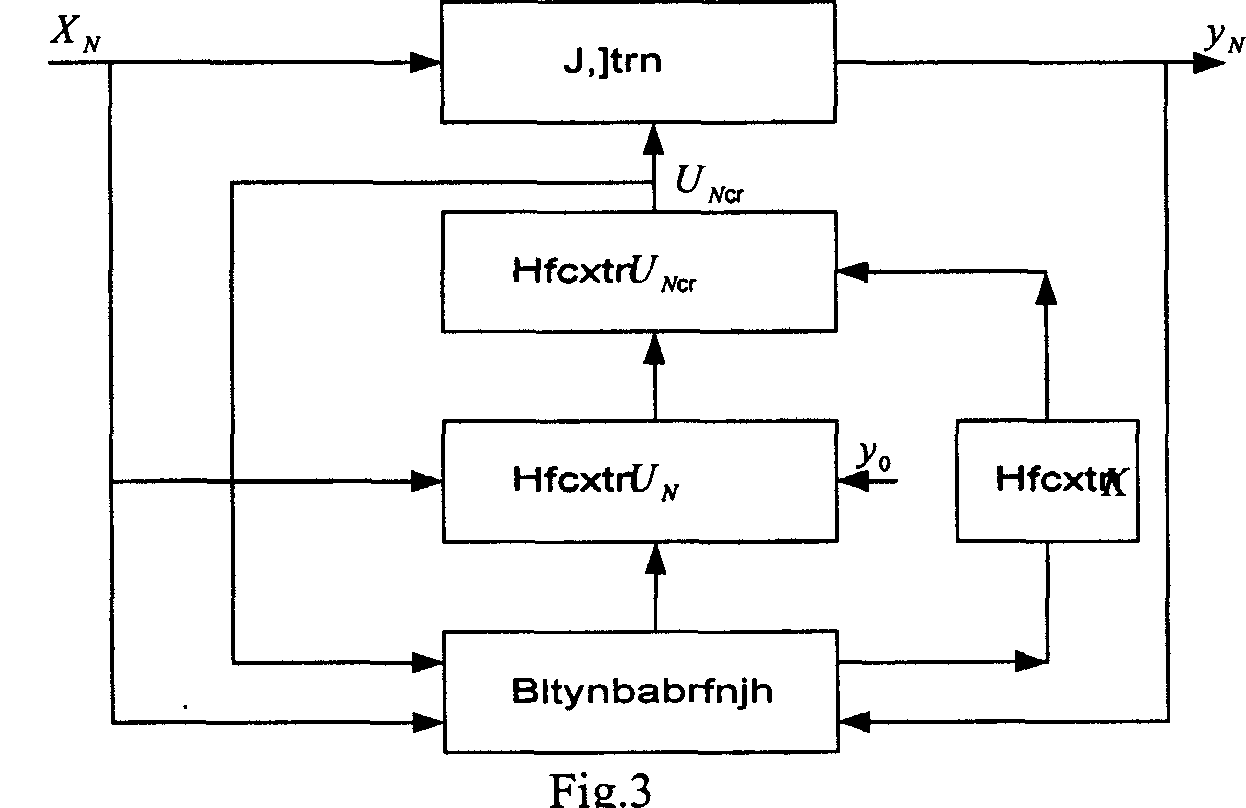
The chart envisages to get information about input and output values, evaluation of model parameters, forecast of output value, determination of correcting factor and calculation of corrected control impact. All the procedures are carried out by ACS.
References:
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|