 |
||
Stankevich L.A., Timakin D.L.
Russia, St. Petersburg, SPbSTU, dtimakin@mail.ru
COGNITIVE CONTROL SYSTEMS
Cognitive systems are a new progressive area that appeared at the intersection of investigations in distributed artificial intelligence, machine learning and neurobiology. In this paper is briefly described a structure of a complex cognitive control system and suggested three possible models of the activator (image processing module in the cell).
–°—В–∞–љ–Ї–µ–≤–Є—З –Ы.–Р., –Ґ–Є–Љ–∞–Ї–Є–љ –Ф.–Ы.
–†–Њ—Б—Б–Є—П, –°–∞–љ–Ї—В-–Я–µ—В–µ—А–±—Г—А–≥, –°–Я–±–У–Ґ–£, dtimakin@mail.ru
–Ъ–Ю–У–Э–Ш–Ґ–Ш–Т–Э–Ђ–Х –°–Ш–°–Ґ–Х–Ь–Ђ –£–Я–†–Р–Т–Ы–Х–Э–Ш–ѓ
–Ъ–Њ–≥–љ–Є—В–Є–≤–љ—Л–µ —Б–Є—Б—В–µ–Љ—Л вАУ —Н—В–Њ –љ–Њ–≤–Њ–µ –њ—А–Њ–≥—А–µ—Б—Б–Є–≤–љ–Њ–µ –љ–∞–њ—А–∞–≤–ї–µ–љ–Є–µ, –≤–Њ–Ј–љ–Є–Ї—И–µ–µ –љ–∞ —Б—В—Л–Ї–µ –Є—Б—Б–ї–µ–і–Њ–≤–∞–љ–Є–є –≤ –Њ–±–ї–∞—Б—В—П—Е —А–∞—Б–њ—А–µ–і–µ–ї–µ–љ–љ–Њ–≥–Њ –Є—Б–Ї—Г—Б—Б—В–≤–µ–љ–љ–Њ–≥–Њ –Є–љ—В–µ–ї–ї–µ–Ї—В–∞, –Љ–∞—И–Є–љ–љ–Њ–≥–Њ –Њ–±—Г—З–µ–љ–Є—П –Є –љ–µ–є—А–Њ–±–Є–Њ–ї–Њ–≥–Є–Є. –Т –і–Њ–Ї–ї–∞–і–µ —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ—В—Б—П –Њ–±–Њ–±—Й–µ–љ–љ–∞—П —Б—В—А—Г–Ї—В—Г—А–∞ —Б–ї–Њ–ґ–љ–Њ –Њ—А–≥–∞–љ–Є–Ј–Њ–≤–∞–љ–љ–Њ–є –Ї–Њ–≥–љ–Є—В–Є–≤–љ–Њ–є —Г–њ—А–∞–≤–ї—П—О—Й–µ–є —Б–Є—Б—В–µ–Љ—Л, –Є –њ—А–µ–і–ї–∞–≥–∞—О—В—Б—П –≤–Њ–Ј–Љ–Њ–ґ–љ—Л–µ –Љ–Њ–і–µ–ї–Є –∞–Ї—В–Є–≤–∞—В–Њ—А–∞ (–≤–љ—Г—В—А–Є–Ї–ї–µ—В–Њ—З–љ–Њ–≥–Њ –Љ–Њ–і—Г–ї—П –њ—А–Њ—Ж–µ—Б—Б–Є—А–Њ–≤–∞–љ–Є—П –Њ–±—А–∞–Ј–∞).
Cognitive control systems (CCS) are a new class of the learning intelligence systems [1]. In general the functional network components of the CCS are realized on neural like elements which form structures with four levels:
Level 1 - project networks consisting of limited sets of cognitive centers like the cells, nucleuses and local networks; they are included in the overlapped networks;
Level 2 - local networks consisting of sets of cognitive centers like the cells and nucleuses; they are included in the project networks;
Level 3 - nucleuses consisting of sets of cognitive centers; they included in the local networks.
Level 4 - cells, which are undivided cognitive centers; the cells included in nucleuses and local networks.
That structure can formally be represented by the relation вАЬconsвАЭ (connect of structure) [2]:
CCSs = (CN1,вА¶, CNi,вА¶, CNI) ;
CNi = cons(вА¶, PNj[1](вА¶, CCk[2](вА¶, CCl[3](вА¶, CCm[4], вА¶)вА¶)вА¶)вА¶) ;
CCm[4] = C ; m=1,вА¶,M ;
CCl[3] = C or N ; l=1,вА¶,L ;
CCk[2] = C or N or LN ; k=1,вА¶,K ;
PNj[1] = C and N and LN ; j=1,вА¶,J , ( 1 )
where CCSS вАУ the structure of the cognitive control systems (CCS); CNi (i=1,вА¶,I) вАУ overlapped networks; CC - cognitive center; C - cell; N - nucleus; LN - local network; PN - projective network.
The upper indexes designate the appropriate nested layer.
It can be offered three variants of CCS topology accordingly to a type of links between cells:
1. The systems with direct images transformation. Transformation of images occurs only in one direction - from inputs to outputs. Once upon a time learned, CCS of direct transformation is stable and can recognize images. There is no dynamic in such systems. Consequently, in such systems doesnвАЩt appear a problem of stability. System with direct transformation is a static non-linear converter.
2. The systems with reconversion of images. ItвАЩs a dynamic system in which recurrent transformation is produced. Such system appears the problem of stability, which in biological analogues solves at the level of independent cells. The dynamic of such system is described by nonlinear differential equations.
3. The systems with nervous-system organization. They are based on the cardinal principles of human nervous system construction. As systems with reconversion of images, this is a dynamic system. The dynamic in such systems is described by complex nonlinear differential equations.
The main unit of all layers of the structure is a cell (informal neuron). The cell is considered to be a minimal element, capable to transform information. An informational model of the cell can be formally represented as the associative fuzzy-logical neural network with layered structure. Formality it can be as:
NM = {X, Hx, St, W, Hy, y}, ( 2 )
where X and y - input vector variables and single output variable; Hx and Hy - hidden variables for activator of the module; St and W - structure and connection weights for the activator of module. This model is executes any vector-vector mapping X ¬Ѓ y on many examples (patterns) with learning.
This informational model is supported by the functional model of the cell
C = (IG, A(a1,вА¶, an, S, W), DG, TC), ( 3 )
where IG - informational granulator forming the set Hx; A(*) - activator consisting of the set of activator's elements ai (i=1,вА¶,N); these elements are doing transformation of the informational granules and composing the set Hy according to the links S and weights W; DG - degranulator, which form the output parameter y; TC - adjuster composing the collection of the links S and weights W under circumstances of the cell tuning for the proper information map X ¬Ѓ y.
In according to this formalization the cell accepts and transforms information at granular mode. That's means that cell compares the current value of the input parameter to a priory defined granules of the parameter. The granule's boundaries can be implicit, fuzzy or random. The estimations of the parameters on suitability input values to granules are transformed in the activator. Activator is the layered associative structure composed of the activator elements, having such basis functions as unity, intersection, inversion and weigh. Using that complete set of operations, it's possible to store associatively and realize any input-output maps.
We can introduce three models of the activator [3].
1. Projection model of the activator. ItвАЩs the simplest from all developed structures.
Let m j(xi) be the value of the j-th membership function of the i-th input signal, m i(y) вАУ the value of the i-th membership function of the output signal. Then, the function, realized by the activator can be represented as:
![]() , (4)
, (4)
where n вАУ the number of inputs; wij вАУweight coefficient; ki вАУ the number of terms on i-th input; l вАУ index corresponding to the first term of the r-th output; p вАУ index corresponding to the first term of the i-th input.
The most effective way of projection model learning is application of a genetic algorithm. The process of the learning consists in tuning of weight coefficients.
This model has serious limitations in the range of application. It canвАЩt be learned to some kinds of image transformation where full information canвАЩt be stored in projections.
Here are the advantages of the structure: (i) low requirements to available memory; (ii) simplicity of the structure; (iii) high ability to generalization.
Here are disadvantages of the structure: (i) applicability to a limited class of problems, in which projections allow to keep full information about input-output transformation; (ii) impossibility of using simple learning algorithms.
2. Grid model of the activator. This model is universal as regards to ability to realize almost any input-output image transformation.
Let m ki(Xi) be the value of the ki membership function of the i-th input signal, m (y) - the value of output membership function. Then, the function, realized by the activator can be presented in the following form:
![]() (5)
(5)
where n вАУ the number of inputs; wiвА¶j вАУ weight coefficient; mi вАУ the number of terms on i-th input. For learning can be used simple algorithm of weight correction.
Here are advantages of the structure: (i) simplicity of the structure and learning algorithm; (ii) versatility of structure, in the sense of abilities to realize practically any continuous function.
Here are disadvantages of the structure: (i) redundancy of internal structure and connected with this high requirements, which object presents to the volume of the memory; (ii) low ability to generalization.
3. Cluster model of the activator. This model does not require the preliminary set of input terms since they are formed dynamically on the base of examples. And what is more when we use cluster model we can manage without degranulator and send output of the activator directly to the output of the cell. In such case we lose on accuracy of transformation, but save on consumed recourses. Thereby, occurs certain departure from standard principles of fuzzy-logical systems building.
Let m j(xi) be the value of the j-th membership function of the i-th input signal. Then, the function, realized by the activator can be represented as:
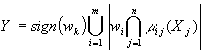 , (6)
, (6)
where n вАУ the number of inputs; m вАУ the number of examples; wi вАУ weight coefficient corresponding to i-th term; k вАУ number of the defining term.
Adjusting of weight coefficients and coordinates and defining bounds and centers of terms are realized during the learning of the activator.
Here are advantages of the structure: (i) simplicity of the structure and learning algorithm; (ii) versatility of structure, in the sense of abilities to realize practically any continuous function; (iii) high ability to generalization; (iiii) low requirements to available memory.
Here are disadvantages of the structure: (i) some difficulties for hardware realization.
The cluster model is the most suitable for using in the CCS. This model combines advantages of grid and projection systems and unites versatility with low memory requirements.
In order to work properly the topology of the CCS must be organized according to preliminarily defined goal of the control in a defined environment. By analogy with natural systems the main principle of topology forming is a self-organization.
The self-organization is a complex process including self-assemblage, self-learning and self-update of the system.
Self-assemblage is the first stage of a self-organization. ItвАЩs a search procedure in the space of possible elements and the links between them.
Self-learning is an optimization procedure. It consists in tuning structure parameters and functions in order to provide adequate behavior of CCS in a continuously changing environment.
Self-update is a process of updating genetic information accumulated in CCS. System uses this information at a self-assemblage and a self-learning phases to direct searching and optimizing procedures.
The process of self-organization can be realized it three ways.
The main purpose of CCS is a multi-channel complex synergetic control, similar to that, which is provided by central nervous system of a human. The range of application of CCS is extremely wide. It varies from synergetic control of an artificial hand, where each finger must work in according to others to provide an execution of a common task, to application in expert systems for forecasting of stock prices.
Reference
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|