Russian Federation,. Pskov, PPI SP STU

Российская Федерация, г. Псков, ППИ СПбГТУ

Решение задач анализа, синтеза и моделирования оптимальных систем управления в условиях неполной априорной информации встречает ряд сложностей.

При исследовании линеаризованных систем не всегда удается найти полное описание условий нестабильности работы системы [1]. Подобные задачи обычно реализуются либо адаптивным, либо робастным подходами.

Плохие динамические свойства контура адаптации часто становятся непреодолимым препятствием использования принципа адаптации. Что касается робастных систем, то они не способны оптимально перестраиваться вслед за изменением случайных возмущений, как со стороны внешних воздействий, так и со стороны собственных параметров системы.

Вместе с тем можно синтезировать систему с постоянными параметрами таким образом, чтобы при действии указанных возмущений качество работы системы оставалось близким к оптимальному. Для этих целей разработан прикладной метод проектирования оптимальных систем по быстродействию [2]. Метод, именуемый методом варьирования свободных функционалов, обладает широкими аналитическими возможностями как для проектирования принципиально нового класса оптимальных конечно-временных регуляторов (КВ-регуляторы) и систем управления, так и моделирования этих систем.

Характер и сложность процесса моделирования оптимальных систем по быстродействию зависит от методов, которые были использованы при построении этих систем. Практическое применение принципа Л.С.Понтрягина и метода динамического программирования Р.Беллмана сталкивается с большими трудностями вычислительного характера из-за того, что процесс построения оптимального управления сводится к решению краевой задачи для обыкновенных дифференциальных уравнений, либо дифференциальных уравнений в частных производных. В связи с этим вычислительная процедура моделирования таких систем в условиях некоторой нестабильности её собственных параметров и характеристик внешних воздействий еще более усложняется.

Более простой и удобной формой моделирования обладает метод варьирования свободных функционалов. Наиболее важной характерной особенностью метода является введенная новая вариация интегрального типа

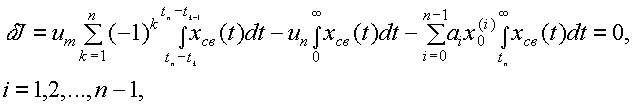(1)

где - номинально заданное управление; - максимально-допустимое варьируемое управление; - свободная составляющая переходного процесса ; - начальные значения управляемой переменной и её производных; - коэффициенты зависящие от параметров объекта управления.

В вариации (1) первый функционал представляет собой закон управления

(2)

Из выражений (1) и (2) следует, что для решения задачи оптимального быстродействия необходимо найти моменты переключения . В принципе максимума Понтрягина проблема моментов переключения управления решается с помощью вспомогательной функции y (t), которая вместе с управлением составляет часть функции Гамильтона

Однако математическая процедура нахождения функции y (t) представляет собой сложную задачу из-за того, что отсутствует начальное условие этой функции. Предложенный подход в виде конечно-временного функционала (2) обладает двумя преимуществами. В нем выделены отдельно переключения , и во-вторых, подынтегральные функции являются свободными составляющими переходного процесса. Интегралы (1) и (2) , как правило, являются типовыми интегралами.

Второй интеграл вариации (1) является исходным функционалом с той же свободной составляющей, но с пределами интегрирования от 0 до для номинально- заданного управления и от до для начальных условий.

Выражения (1) отличается от всех известных вариаций интегрального типа. В ней варьирование функционала осуществляется за счет изменения пределов интегрирования, тогда как в известных вариациях классического вариационного исчисления варьирование функционала выполняется путем изменения подынтегральной функции.

Уравнение (1) используется для построения оптимального программного управления на конечном интервале времени без учета возмущений со стороны изменения параметров объекта и входных воздействий.

Однако реальное движение системы, как правило, будет отличаться от программного по многим причинам: из-за неполной информации о внешних возмущениях, неточности модели объекта и т.д. (рис.1). Поэтому необходимо еще учесть отклонения управляемой переменной и её производных от программного

(3)

и отклонение реального управления от программного

(4)

В результате получаем уравнение возмущенного движения с учетом неточности модели объекта на интервале времени

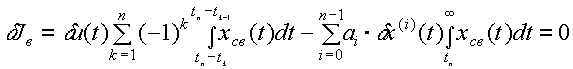(5)

Выражения (1? 5) составляют основу математической модели моделирования линейных оптимальных систем управления по быстродействию. К этим выражениям необходимо еще добавить временные функции переходного процесса и их производные . Причем, учитывая, что моделирование в основном выполняется в цифровом варианте, то следует перейти к решетчатым функциям , где T - период дискретности.

+Графически процесс моделирования представлен на рис.1.

Математическая модель задатчика оптимального программного управления представлена уравнением (1), с помощью которого находятся моменты переключения.

Математическая модель задатчика оптимального или робастного регулирования описывается уравнением (5) с учетом (3,4). Он служит для определения дополнительного сигнала управления с целью обеспечения стабилизирующего движения оптимальной траектории системы.

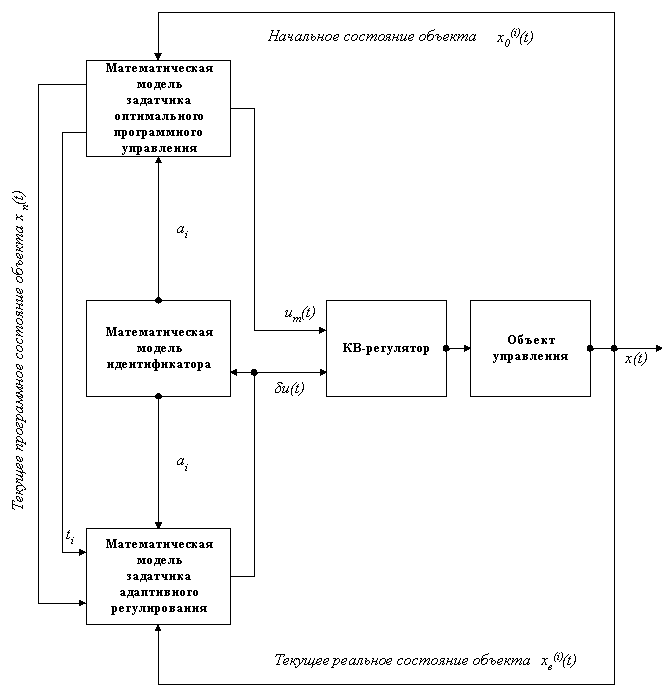
Рис. 1. Функциональная схема интеллектуального процесса моделирования.

Математическая модель идентификатора строится на основе методов планирования экспериментов. Например, с использованием Д- оптимальных планов. С учетом априорных сведений о возможных границах изменения параметров объекта строится план эксперимента. При наличии возмущающего сигнала на задатчики поступают соответствующие значения параметров .

Оценка параметров объекта считается законченной при достижении заданной точности : .

Эта методика применима и для моделирования нестационарных систем если на временном интервале идентификации сохраняется стационарность процесса.

Моделирование оптимальной системы методом варьирования свободных функционалов было проведено в лабораторных условиях с использованием программного пакета Mathcad

Данная методика моделирования позволяет оценивать параметры объекта с высокой степенью точности при условии параметрической неопределенности.

Литература

1. Бесекерский В.А., Ефимов Н.Б. и др. Микропроцессорные системы автоматического управления. / Под ред. В.А.Бесекерского // Л. Машиностроение,1988г.
2. Авдеев О.Н. Метод варьирования свободных функционалов и его применение в задачах оптимального синтеза систем автоматического управления / Под ред. К.А. Пупкова. // СПб. СПбГТУ,1996. 156с.