Russia, St-Petersburg, SPII RAS, alexandr@mail.iias.spb.su

For the purpose of pattern recognition a new Pseudo-Ternary Number System is introduced, which ensures the image representation of filming conditions independently. The variations of filming conditions are simulated within the framework of arbitrary local image transformations, which do not modify the ratios of adjacent intensities ('more', 'equal' or 'less').

Россия, Санкт-Петербург, СПИИРАН, alexandr@mail.iias.spb.su

В докладе вводится понятие псевдотроичной системы счисления и решается проблема автоматического обнаружения и идентификации объектов при изменении условий съёмки. Изменчивые условия моделируются изоморфными преобразованиями изображения, допускающими произвольные изменения перепадов яркости между соседними пикселами без нарушения исходных яркостных соотношений больше/равно/меньше.

1. Введение

Работа относится к области обработки видеоданных и связана с созданием интеллектуального комплекса адаптивного (автоматического, ассоциативного) распознавания изображений ИКАР [1-2], практическая реализация которого начата в 000 “ИстаВидеоТесТ” (Санкт-Петербург).

Формальной основой работы является псевдотроичная система счисления (рис.1), в которой неотрицательные целые числа I₀ раскладываются по степеням 2, как в обычной двоичной системе, но записываются в виде последовательности цифр от 0 до 2, как в троичной системе



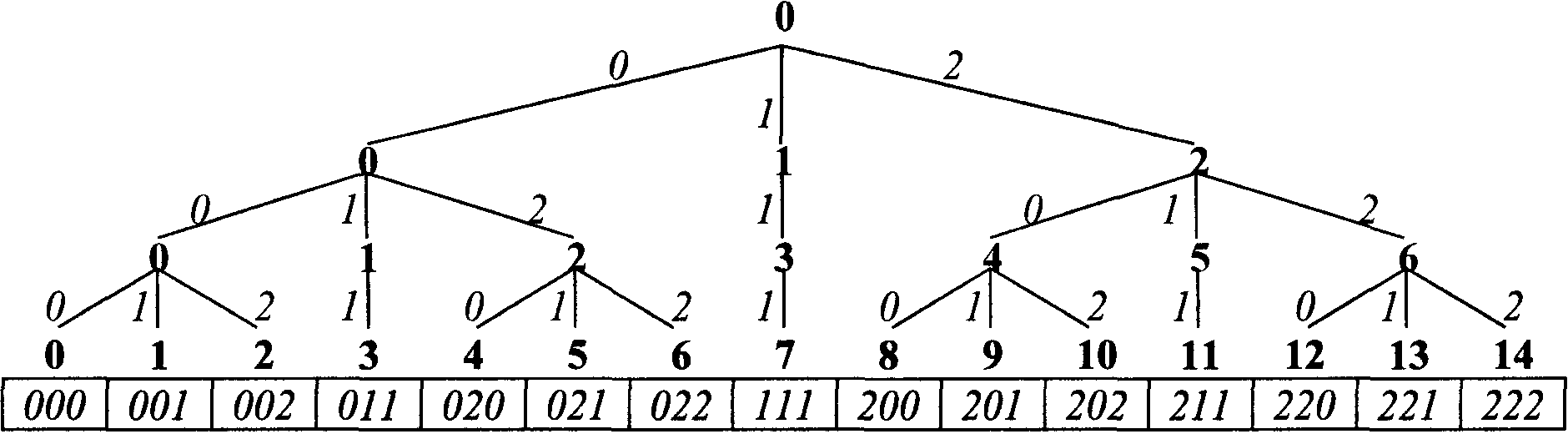
Рис. 1. Псевдотроичная система счисления неотрицательных целых чисел



где при нечётном при чётном квадратные скобки обозначают “целую часть”.

В отличие от классических систем счисления [З], однозначность псевдотроичного представления чисел достигается тем, что допускаются не все сочетания цифр (чётные числа описываются чередованием 0 и 2, а нечётные - чередованием 0 и 2 с заключительной последовательностью из одних 1).

2. Инвариантное псевдотроичное представление изображения

Не зависящее от изоморфных преобразований псевдотроичное представление разбиения изображения на сегменты из пикселов равной яркости вычисляется посредством построения, так называемой, карты минимумов и карты максимумов (рис.2).

Вначале поле искомого инвариантного представления заполняется значениями яркости, равными 0.

При получении карты минимумов исходные локальные минимумы заполняются нулевыми яркостными значениями, затем среди остальных находятся следующие, которые заполняются 1, и далее по порядку до тех пор, пока все точки х,у карты не окажутся помеченными некоторыми номерами b(х,у), показанными на рис.2 (b) соответствующими значениями яркости. Аналогично строится карта максимумов, яркостями которой служат номера локальных максимумов с(х,у), представленные на рис.2 (с) в негативном изображении. Формирование псевдотроичного представления заключается в том, что его яркостные значения d(x,y) удваиваются и увеличиваются на = 0, 1 или 2 при b(х,у) < с(х,у), b(х,у) = c(x,y) или b(х,у) > с(х,у), соответственно.

Процедура циклически повторяется до получения псевдотроичного представления рис.2 (d) с яркостями I₀(х,y), которое изоморфно исходному изображению. При этом каждый яркостный сегмент текущего псевдотроичного представления определяет обработку самостоятельного участка изображения [4], что позволяет при построении ограничиваться сравнением между собой смежных сегментов изображения, которые имеют в псевдотроичном представлении одинаковую чётную яркость.

Преобразование яркостей I₀(x,y) результирующего псевдотроичного представления рис.2 (d) по рекуррентным соотношениям п.1 позволяет в обратном порядке воспроизвести этапы построения и аппроксимировать исходное изображение в ...31, 15, 7 и 3 яркостных градациях. При этом I₀(x,.у) зависит только от знаков перепадов яркости между соседними пикселами исходного изображения I(х,у). Чётными яркостями в псевдотроичном представлении описываются укрупнённые локальные экстремумы, состоящие из нескольких сегментов исходного изображения, а нечётными - отдельные пограничные сегменты, которые находятся между укрупнёнными локальными максимумами и минимумами и имеют промежуточную яркость.





(с) (d)

Рис. 2. Изоморфные изображения: (а) - изображение, (b) - карта минимумов,

(с) - инвертированная карта максимумов, (d) - псевдотроичное представление

3. Компактная адаптивная иерархическая сегментация

Под иерархией (иерархической сегментацией) понимается последовательность разбиений изображения на вложенные сегменты. Компактная иерархия ([4]) определяется ограниченным числом вложенных разбиений (уровней сегментации) изображения. При этом составные сегменты на различных уровнях не повторяются, укрупняясь при переходе с "нижнего" уровня на "верхний". Из возможных иерархий сегментов для представления изображения используются адаптивные, которые обеспечивают точную аппроксимацию объектов минимальным числом частей адекватной формы и размеров.

Для автоматизации обработки изображений наиболее эффективно применение компактной адаптивной иерархической сегментации, которая объединяет достоинства регулярного пирамидального [5] и многоуровневого адаптивного [6] представлений изображения. Её построение достигается в результате относительно небольшого числа итераций, интерактивная процедура аппроксимации объектов при обучении программного комплекса [1] и автоматическое "конструирование" объектов из сегментов с различных уровней в автономном режиме требует выполнения ограниченного числа операций. Для оптимизации вычислений в реальном времени предусмотрены специальные структуры данных [7].

Изоморфное псевдотроичное представление изображения при рекуррентной арифметической редукции яркостных значений по п.1 обеспечивает получение варианта компактной адаптивной иерархии рис.3, который открывает неожиданную возможность выделения объектов. Согласно п.1 с уменьшением градаций число пикселов чётной яркости, очевидно, монотонно растёт. Обычно на изображениях с фоном чётные пикселы на некотором уровне заполняют область объектов (либо фона). В свою очередь внутри выделенных объектов, как на отдельных изображениях, могут обнаружиться новые и т.д., что представляет самостоятельный интерес.



20768 сегментов 34194 сегмента

Рис. 3. Представления изображения в 3, 7,15 и 31 градациях псевдотроичной яркости (контрастированы)

4. Заключение

Алгоритм инвариантного представления двумерного изображения на основе псевдотроичной системы счисления переносится на случай одномерных и многомерных гистограммных распределений [8], которые подобно изображению могут представляться в 3, 7, 15 ... градациях встречаемости для повышения устойчивости традиционных и разработки новых методов выделения объектов в программно-измерительных комплексах анализа изображений.

Замещение значения яркости её встречаемостью или некоторым числовым признаком сегмента (площадью, периметром, интегральными координатными моментами и пр.) порождает различные представления изображения, псевдотроичное кодирование которых обеспечивает наглядную интерпретацию обнаружения объектов и оценку адекватности используемых признаков.

Таким образом, с точки зрения автоматизации распознавания основной смысл получения псевдотроичного представления состоит в наглядном преобразовании двумерного изображения независимо от изоморфных преобразований к некоторому стандартному (каноническому) виду, что упрощает дальнейшую обработку и может использоваться также в системах анализа радио- и аудио- сигналов и других, например, системах когнитивной графики.

С математической точки зрения псевдотроичное представление является арифметической моделью изображения, для которой применим аппарат модулярной арифметики [З]. Самостоятельный интерес представляет экспериментальное исследование и интерпретация арифметических и алгебраических унарных и дуальных операций с изображениями, осуществляемых в рамках изоморфных преобразований.

Для пиктографической интерпретации [2, 9] результатов адаптивной обработки инвариантного представления видеоданных и создания символьного языка управления интеллектуальными комплексами ИКАР с участием человека и при автономном взаимодействии, по-видимому, применим обобщённый аппарат мультипликативного и аддитивного симметрирования [10] матриц, что определяет перспективу дальнейших исследований.

[1] М.В.Харинов Интеллектуальный комплекс автоматического распознавания изображений на базе ПЭВМ (ИКАР) // Компьютерные технологии в науке, проектировании и производстве / Тез. докл. 1 Всерос. научно-технической конф. - Нижний Новгород., 1999.-ч.9.-С.22-23.

[2] М.В.Харинов Перестановочная и скрытая симметрия на примере изоморфных матриц Адамара. Приложения в области искусственного интеллекта // Средства математического моделирования / Труды Второй межд. конф. - С.-П.: изд-во СПбГТУ, 1999. -т.5 - С 247-254. [3] Д.Кнут Искусство программирования для ЭВМ. Получисленные алгоритмы, М.:

Мир, т.2, 726 с.

[4] M.V.Kharinov, M.M.Nesterov "Intelligent Program for Automatic Image Recognition based on Compact Object-Fitting Hierarchical Image Representation in terms of Dynamic Irregular Ramified Trees" / Специальный выпуск межакадемического бюллетеня МАИСУ № 12-С, - С.-П., 1997. -С. 1-35.

[5] V.V.Alexandrov, N.D.Gorsky, "Image Representation and Processing. A Recursive Approach" Dodrecht /Boston/London: Kluwer Academic Publishers, 1993., -157 p.

[6] V.V.Alexandrov, M.V.Kharinov, "Dynamic Adaptive Data Structure in Image Recognition" / Специальный выпуск межакадемического бюллетеня МАИСУ № 12-С, - С.-П., 1997. -С. 36-44.

[7] М.В.Харинов Разработка динамических структур данных системы автоматизированного распознавания изображений . Автореф. Дис. канд.технич.наук.- С.П. 1993. -20с. [8] У.К Прэтт Цифровая обработка изображений. М.: Мир, 1982. T.I.-2. 792 с. [9] В.В.Александров, Р.И.Полонников, Е.И.Трофимов Оптоэлектронные устройства и перспективы их использования в радиоэлектронной аппаратуре/УЭлектронно-лучевые и фотоэлектронные приборы./Труды конф. по электронной технике, Вып.5 (31), изд. ЦНИИ "Электроника", 1971., 1бс.

[10] Н.А.Балонин, Л.А.Мироновский Линейные операторы динамической системы// АиТ, 2000., -15с. (в печати).