Россия, Саратов, СГТУ

Рассмотрена задача моделирования методом реконструкции динамических систем по временным рядам. Отмечены недостатки существующих подходов. Показана возможность и преимущества решения подобной задачи на нейронных сетях. Особенности подхода исследованы на примере реконструкции системы по пульсограммам. Приведены результаты экспериментов на сети Хопфилда.

Многие проблемы управления, прогнозирования, распознавания образов связаны с задачей разработки математических моделей. Можно выделить два подхода к ее решению. Первый подход заключается в разработке модели, исходя из известных физических принципов и законов функционирования моделируемой системы. При втором подходе модель строят по временной реализации некоторой переменной состояния системы. В этом случае предполагается, что математическая модель представляет собой систему обыкновенных дифференциальных уравнений, приближенно описывающую эволюцию переменных состояния системы. Построение модели, или реконструкция динамической системы (ДС), собственно состоит в восстановлении модельных уравнений анализируемой системы, которые с заданной точностью способны воспроизводить экспериментально полученный временной ряд.

Остановимся более подробно на втором подходе, который наиболее применим к исследованию сложных систем, доступных для изучения только по своим реализациям. Наиболее ярким примером здесь являются медико-биологические системы, где достижения теории динамических систем могут находить свое практическое применение. В качестве примера рассмотрим задачу реконструкции динамической системы с целью диагностики и прогнозирования патологий по пульсограммам. Так, имея пульсовый сигнал (пульсограмму) и решая задачу реконструкции, можно оценить состояние здоровья человека, выявить патологии.

В данном случае интерес к пульсограммам обусловлен тремя причинами:

1. пульсовый сигнал является достаточно сложным по форме и обладает некоторыми особенностями, которые выделяют его из реализаций других колебательных систем, демонстрирующих хаотическое поведение;
2. данный сигнал легко доступен и позволяет эффективно проводить диагностику;
3. метод диагностики по пульсограммам системы имеет тысячелетнюю историю, его эффективность проверена веками.

Существующие методы обработки пульсограмм основаны на определении характерных точек, изгибов, величин пиков, спектральном анализе. Однако мозг человека плохо приспособлен для выполнения арифметических операций. Мозг создает на своих нейронных сетях образы и оперирует ими. С достоверностью можно предположить, что, ощущая пальцами пульс, тибетские медики реконструировали в мозгу динамическую модель составляющей человеческого организма.

Следует отметить, что наблюдаемые временные реализации представляют такие установившиеся режимы, которые достигаются в пределе при t ® ? . Это подразумевает наличие в фазовом пространстве системы притягивающего предельного множества точек - аттрактора. Поэтому задача реконструкции подразумевает задание подходящего фазового пространства и формирование предельных множеств, соответствующих исходной временной реализации. Этой задаче посвящено достаточно большое количество публикаций (например, [ 1] и библиография в ней).

Изложенные в [ 1] подходы к проблеме реконструкции ДС характеризуются следующими основными недостатками:

• выбор полиномиальной нелинейности не всегда оправдан
• результирующие уравнения получаются негрубыми, то есть малое изменение их параметров приводит к уходу фазовой траектории в бесконечность;
• небольшое зашумление экспериментальных данных может существенно исказить результаты.

Нейронные сети являются более гибким аппаратом моделирования [2]. Аппроксимация нелинейностей осуществляется нейронными сетями. Каждый нейрон сети реализует простую нелинейную функцию одного аргумента j ( y). Нейрон имеет несколько входов, на которые поступает вектор сигналов X. Значимость входов одного нейрона определяется вектором весов w. Для сети из n нейронов, на входы которых подается вектор сигналов X, будем иметь n векторов w, которые образуют матрицу весовых связей W.

Аргументом нелинейной функции нейрона является скалярное произведение (X,W), т.е. j (y) = j [(X,W)]. Здесь j - это сигмоидная функция активации нейрона, j = 1 ¤ ( 1 + e^-y) . Результат преобразований передается на входы других нейронов. Нелинейное преобразование исходного образа X={x₁,x₂,…,x_n} происходит по правилу

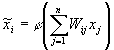Нейронная сеть представляет суперпозиции простых функций одной переменной и их линейные комбинации и производит аппроксимации нелинейных функций [ 3] . Так же, как и в случае с полиномами, матрица W ищется исходя из условия минимизации ошибки аппроксимации. Главное отличие заключается в том, что структура матрицы W (симметрия и знаки элементов) задается первоначально произвольно. На последующих шагах аппроксимации значения элементов определяются, например, методом наименьших квадратов. Избыточность информации в сетевых связях обеспечивает грубость аппроксимации при высокой точности.

Помимо аппроксимации нелинейностей нейронные сети являются универсальным средством представления оператора эволюции. В этом случае правила преобразования образа (1) заменяются системой нелинейных дифференциальных уравнений нейронной динамики

Здесь V_i(t) - состояние i - го нейрона в момент времени t; b_i -усиление; матрица W_ij и функция j имеют тот же смысл, что и раньше. В зависимости от выбора коэффициентов b_i, c_i получаются сети разных типов.

Для динамических систем подобного типа теорема Коэна-Гроссберга гарантирует существование областей притяжения - аттракторов. Эти области формируются в процессе синтеза матрицы W на основе исходных или эталонных образов. Эволюция состояния реконструированной нейронной сети приводит ее в область или точку равновесия. Эта область характеризуется локальным минимумом энергии, координаты которого соответствуют эталонному образу.

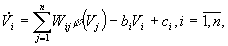Из уравнения (2) можно получить следующее

где b_i - коэффициенты обратной связи, c_i - внешнее воздействие на i - й нейрон. Полученное уравнение описывает сеть Хопфилда. Эта сеть выбрана для реконструкции динамической системы по данным пульсограмм.

Сети Хопфилда используются для запоминания статических образов, которые представляют точки аттракторов в фазовом пространстве нейронной системы.

Временные реализации реконструируемых систем представляют предельные множества другого типа. В простейшем случае - это предельный цикл. Возможны также более сложные образования. Поэтому особенность реконструкции на сетях Хопфилда заключается в формировании не точки равновесия, а предельного цикла. Эта особенность налагает дополнительные условия на правила синтеза матрицы W [4]. В частности, в экспериментальных исследованиях матрица была выбрана несимметричной. Помимо этого, структура сети учитывала то, что исходный сигнал является почти периодическим. Количество нейронов определялось из выражения n = (T/t )+1, где T - период исходной реализации, t - дискретность съема информации.

Были проведены две серии экспериментов. Первая серия экспериментов базировалась на теореме Такенса [ 5] . В качестве эталонных образов выбирались исходная реализация вида

и ее модификации, полученные простой перенумеровкой a_i = a_i+1. Таким образом, сети было представлено n эталонов.

Вторая серия экспериментов основывалась на последовательном дифференцировании исходной временной последовательности. В качестве фазовых переменных использовались значения a(t), a'(t) и a''(t). Поэтому сеть содержала 3n элементов. Выбор трехмерного пространства обусловлен тем, что оценка размерности Хаусдорфа оказалась равна 2,75.

Экспериментально доказана возможность реконструкции ДС на нейронных сетях в обеих сериях экспериментов. Решения реконструированных уравнений модели качественно повторяют основные особенности исходного сигнала, однако сходство в деталях проявляются не всегда. Кроме того, предельные циклы возникали только при определенных численных значениях исходных реализаций. Отметим, что вторая серия экспериментов менее чувствительна к числам.

Дальнейшие исследования необходимо направить на совершенствование методики определения матрицы связи и структуры сети, которые гарантированно приводили к предельным циклам.

Литература

1. Анищенко В.С., Вадивасова Т.Е., Астахов В.В. Нелинейная динамика хаотических и стохастических систем. Фундаментальные основы и избранные проблемы /Под ред. В.С. Анищенко. - Саратов: Изд-во Сарат. Ун-та. - 1999. - 368 с.
2. Булдакова Т.И., Суятинов С.И. Нейрокомпьютерные системы: Учеб. пособие. - Саратов: Изд-во Сарат. Гос. Техн. Ун-та. - 1999.-96 с.
3. Нейроинформатика /А.Н.Горбань, В.Л.Дунин-Барковский, А.Н.Кирдин и др. - Новосибирск: Наука. Сибирское предприятие РАН, 1998. - 296 с.
4. Петрякова Е.А. Нейронные сети Хопфилда с несимметрической матрицей коэффициентов связи между нейронами //Изв.вузов. Приборостроение. - 1994. - Т. 37. - № 3-4. - С.24-32.
5. Takens F. Detecting strange attractors in turbulence // Dynamical Systems and Turbulence / Eds. D. Rang and L.S. Young. Lect. Notes in Math. - 1980.- V. 898. - P. 366-381.