 |
||
ИССЛЕДОВАНИЕМЕТОДОВ ПРОГРАММИРОВАНИЯ ОПТИМАЛЬНОЙ ТРАЕКТОРИИ ДВИЖЕНИЯ ТРАНСПОРТНЫХ СРЕДСТВ
Санкт-Петербургский государственный технический университет
Козлов В.Н., Бугаева Е.В.
Характерной чертой современной эпохи является бурный взрыв исследовательского интереса к экстремальным задачам, т.е. задачам определения наибольшего и наименьшего значений, оптимальных условий протекания процессов и т.д. Следует подчеркнуть, что подобные задачи встречались в истории человечества в том или ином виде начиная ещё со времён античности. Однако именно на современном этапе развития экстремальные задачи заняли доминирующее положение прежде всего вследствие ограниченности природных и материальных ресурсов, необходимости жёсткой экономии энергии и материалов, других причин. На протяжении всего своего существования человечество проявляло интерес к проблеме поиска оптимального маршрута, пытаясь использовать свои знания для решения различных задач навигации. В качестве примеров можно упомянуть задачи: прохождения лабиринта [1], Гамильтона о замкнутом маршруте (кругосветное путешествие) [1, 2], коммивояжера [2] и т. д. С появлением ЭВМ решение данной проблемы приобрело новое качество: стала возможной практическая реализация методов планирования траектории пути в различных областях техники и, в частности, интеллектуальных системах [3-6]. Это послужило толчком к совершенствованию уже известных методов и разработке новых. Поднятая проблематика находит широкое применение в таких современных приложениях, как организация системы управления робототехнических комплексов (планирование маршрута движения автономных транспортных средств, планирование перемещения охвата манипулятора [3-6]), системы управления динамическими объектами (автоматизация судовождения [7], бортовые системы управления полётом [8]).
Рассмотрим задачу программирования оптимальной траектории движения для бортовых систем управления полётом. Оптимальность определяется по следующим параметрам:
- реализация высокой степени безопасности полёта;
- обеспечение максимальной манёвренности летательного аппарата;
- выведение в ранее определённый район посадки с заданной точностью;
- выполнение поставленной перед экипажем задачи за минимальный промежуток времени.
Следует отметить, что указанные вопросы, достаточно успешно решаемые в настоящее время для нормальных условий полёта, применительно к экстремальным режимам и условиям развиты слабо. С технической точки зрения движение по оптимальному маршруту можно достичь путём введения в систему ручного пилотирования устройств, которые автоматически ограничивают отклонение управляемых поверхностей летательного аппарата по сигналам вычислителя, не допуская до критической ситуации при любой манере управления. Дальнейшее усовершенствование бортовых комплексов автоматизированных систем управления полётом позволит экипажу полнее использовать потенциальные возможности самолёта. Аналитически точных методов решения альтернативного управления не существует. Отличительная особенность ранее разработанных процедур поиска оптимального пути заключается в том, что не увеличивается размерность задачи и в свою очередь не может привести к кризисным ситуациям во многих приложениях.
Алгоритм программирования оптимального маршрута построен для решения исследуемой задачи как задачи безусловной оптимизации с использованием метода штрафных функций при постановке задачи и комбинации метода градиентного спуска и теории наилучшего приближения равномерной функции на компактном множестве. Программируемая траектория используется при построении управления эталонной моделью в системе адаптивного управления ТРС.
Разработанный алгоритм программирования оптимального маршрута ТРС характеризуется выбором на карте движения допустимых (безопасных для ТРС и экипажа) траекторий. Идея алгоритма позаимствована из работы Агеева Д.А. и Истратова А.Ю. [9] и развита на случай планирования допустимого "коридора" движения, точек старта и цели соединяются ломаной линией (количество и координаты точек изломов выбираются с учётом координат пунктов посещения). Затем, посредством параллельного и направленного перемещения точек изломов ломаной, используя возможности карты проблемной среды, осуществляется безопасных обход препятствий и строится допустимый "коридор" движения ТРС и в рамках этого "коридора" оптимальная траектории движений ТРС.
При анализе методов решения экстремальных задач и сопоставлении результатов экспериментов, была отмечена необходимость перехода от задачи нелинейного программирования к задаче без ограничений. Известно, что идея метода модифицированных функций Лагранжа и метода штрафных функций состоит в сведении задач оптимизации с ограничениями к задачам без ограничений. К настоящему времени установлены и доказаны условия, благодаря которым метод штрафных функций приводит также как и метод множителей Лагранжа к точке Куна-Таккера, если взять в качестве двойственных переменных частные производные штрафа по фукциям-ограничениям [10 ].
МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ЗАДАЧИ
Пусть карта проблемной среды представлена множеством точек Т = {(xi, ym); i = 1, ..., N;
m=1,...,I},Т![]() R2q1
R2q1![]() P
P![]() T(1=1,…,n) - множество точек (пунктов)
которые необходимо посетить, причём q1 -
точка старта, qn - точка цели, S == {(Ck, Rk
); k = 1, ..., K1} - множество препятствий, где Ck
T(1=1,…,n) - множество точек (пунктов)
которые необходимо посетить, причём q1 -
точка старта, qn - точка цели, S == {(Ck, Rk
); k = 1, ..., K1} - множество препятствий, где Ck![]() Т - центр, а Rk -
радиус окружности, которой аппроксимируется
препятствие. Требуется проложить оптимальный
маршрут из точки старта q1 к точке цели qn,
таким образом, чтобы охватывались все пункты
посещения Р и траектория маршрута и траектория
маршрута не пересекала препятствий S. В качестве
критерия оптимальности предлагается
рассматривать минимум длины проложенной.
Т - центр, а Rk -
радиус окружности, которой аппроксимируется
препятствие. Требуется проложить оптимальный
маршрут из точки старта q1 к точке цели qn,
таким образом, чтобы охватывались все пункты
посещения Р и траектория маршрута и траектория
маршрута не пересекала препятствий S. В качестве
критерия оптимальности предлагается
рассматривать минимум длины проложенной.
Первую компоненту (L) функционала качества можно определить аналогично соответствующей компоненте [9], вид второй (F) и третьей (G) определяется из соотношения пересечения прямой линнии с окружностью в отличие от [9] с помощью элементов векторной алгебры (шаг итерации*). Результаты проведённых исследований позволяют сделать вывод о том, что количество необходимых вычислений сократилось в результате одного шага итерации, с помощью которого определяется и возможность указанного пересечения, и расчет точки изгиба траектории, если пересечение произошло.
МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ЗАДАЧИ КАК ЗАДАЧИ БЕЗУСЛОВНОЙ
ОПТИМИЗАЦИИ
Найти ![]() M(P),
если
M(P),
если
М(Р) = L(P) + ![]() ,
(1.1)
,
(1.1)
где ![]() ,
,![]() - некоторые константы (
- некоторые константы (![]() > 0,
> 0, ![]() > 0), причем
> 0), причем
F(f(P)) == 0, если f(P)![]() 0 для всех k
0 для всех k ![]() К = {1,
2, ..., K1},
К = {1,
2, ..., K1},
F(f(P)) > 0, если f(Р) < 0 хотя бы для одного
k ![]() К;
К;
G(f(Р)) = 0, если f(P)![]() 0 для всех k
0 для всех k ![]() К = {1,
2, ..., K1},
К = {1,
2, ..., K1},
G(f(P)) > 0, если f(P) < 0 хотя бы для одного
k ![]() К;
К;
Первая компонента функционала (2.12) характеризуется величиной
L(M)=![]() , (1.2)
, (1.2)
где |qj – qj+1| - стандартная евклидова метрика в R2
![]() .
.
.
Эта компонента характеризует длину ломаной и минимизируется при сжатии ломаной в точку.
Вторая компонента (1.1) является функцией штрафа на пересечение отрезком ломаной зоны препятствия. Её вид определяется из соотношения пересечения прямой линии с окружностью:
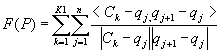 , (1.3)
, (1.3)
где ![]() -
скалярное произведение векторов, которое
вычисляется по формуле
-
скалярное произведение векторов, которое
вычисляется по формуле
![]()
Третья компонента функционала (2.12) - штрафная функция на попадание одной или нескольких точек изломов траектории в зону k-того препятствия:
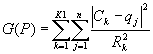 (1.4)
(1.4)
Минимум функционала (1.1) определяет вид ломаной, которая соответствует возможной траектории в рамках выбранных требований. Таким, образом, минимизация длины ломаной производится посредством изменения координат точек
qj для обхода препятствий.СПИСОК ЛИТЕРАТУРЫ
1. Планирование траекторий для мобильных роботов. // Пер. с яп. М.: Всероссийский центр переводов. № Н- 42043, 1987.
2. Кристофидекс Н. Теория графов (алгоритмический подход).//Пер. с англ. М.: Мир, 1978.
3. Автономные мобильные роботы. // Пер. с англ. М.: Всероссийский центр переводов. №Р-4075, 1988.
4. Движущийся робот на Марсе до 2000 года. // Пер. с англ. М. ЦНИИТЭСТРОЙМАШ. №2823,1990.
5. BlidbergD.R. Unmanned Submersible Vechicles. // Workshop on Autonomous Ground Vechicles. Leesburg: VA, 1984.
6. Gilmore J.F. The Autonomous Helicopter Sistem. // SPIE Application of AI. Wachington: D.C., 1983.
7. Чуркин В.И. Оптимальное управление расхождением судов. // Изв. РАН. Теория и системы управления. 1999, №2.
8. Козлов В.Н., Куприянов В.Е., ШашихинВ.Н. и др. Бортовые системы управления полётом. СПб, СПбГТУ, 1999.
9. Агеев Д.А., Истратов А.Ю Нейросетевая реализация задачи поиска оптимального пути. Изв. РАН. Теория и системы управления. 1998. № 1.
10. Карманов В.Г. Математическое программирование. М.: Наука, 1986.
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|