 |
||
|
||
K.A. Pupkov, S. M. Verteshev, O.N. Avdeev, I.O. Avdeev, L.V. Motaylenko, I.A. Poletaev
Russian Federation, Pskov, PPI SP STU
THE APPLIED THEORY And DESIGN TECHNIQUES of NEW CLASSES OPTIMAL, ADAPTIVE, ROBUST And INTELLECTUAL REGULATORS
The new approaches and design techniques of perspective modern classes of regulators, microcontrollers and microcomputers are considered. The variational theory of free functionals and the methods of a design of experiments allow to design systems with an optimal program control, adaptive regulation, active identification and intellectual conversion. |
Пупков К.А., Вертешев С.М., Авдеев О.Н.,Авдеев И.О.,Мотайленко Л.В.,Полетаев И.А.
Российская Федерация, г. Псков, ППИ СПбГТУ
ПРИКЛАДНАЯ ТЕОРИЯ И МЕТОДЫ ПРОЕКТИРОВАНИЯ НОВЫХ КЛАССОВ ОПТИМАЛЬНЫХ, АДАПТИВНЫХ, РОБАСТНЫХ И ИНТЕЛЛЕКТУАЛЬНЫХ РЕГУЛЯТОРОВ
Обсуждаются новые подходы и методы проектирования перспективных современных классов регуляторов, микроконтроллеров и микрокомпьютеров. Вариационная теория свободных функционалов и методы планирования экспериментов позволяют проектировать системы с оптимальным программным управлением, адаптивным регулированием, активной идентификацией и интеллектуальным преобразованием. |
Введение
Вариационная теория свободных функционалов [1] формировалась и продолжает развиваться с учетом концепции построения интеллектуальных систем, сформулированной профессором К.А. Пупковым [2]. Она является прикладной теорией проектирования новых классов оптимальных, адаптивных, робастных и интеллектуальных регуляторов. Ее основной метод варьирования свободных функционалов является аналитическим методом, обладает большими функциональными возможностями решения оптимальных задач. В первоначальном варианте метод варьирования свободных функционалов был ориентирован на построение оптимальных линеаризованных систем управления.
Дальнейшее его развитие показало, что метод позволяет проектировать системы с оптимальным программным управлением, адаптивным регулированием, активной идентификацией и возможностью построения интеллектуальных систем.
На рис.1 представлена функциональная схема научно-исследовательского вычислительного комплекса моделирования и автоматизированного проектирования новых классов оптимальных, адаптивных, робастных и интеллектуальных регуляторов.
В состав комплекса входят: задатчик оптимального программного управления, идентификатор, задатчик адаптивного регулирования, микроконтроллер или микрокомпьютер, интеллектуальный решатель и модель объекта управления.
Методы и модели вариационной теории свободных функционалов
Основным методом проектирования являются метод варьирования свободных функционалов [1,3]. Он обладает относительно простыми и удобными формами математических моделей оптимизации, адаптации и параметрической идентификации.
Модель оптимального программного управления
Для построения модели и алгоритма оптимального программного управления введена система частных вариаций функционалов:
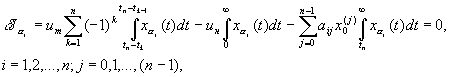(1)
где 
-
номинально-заданное управление; 
- свободная составляющая
переходного процесса, соответствующая корню 
;
- начальные значения управляемой
переменной
и ее
производных; 
-
максимально-допустимое управление; 
- коэффициенты, зависящие от
параметров объекта управления.
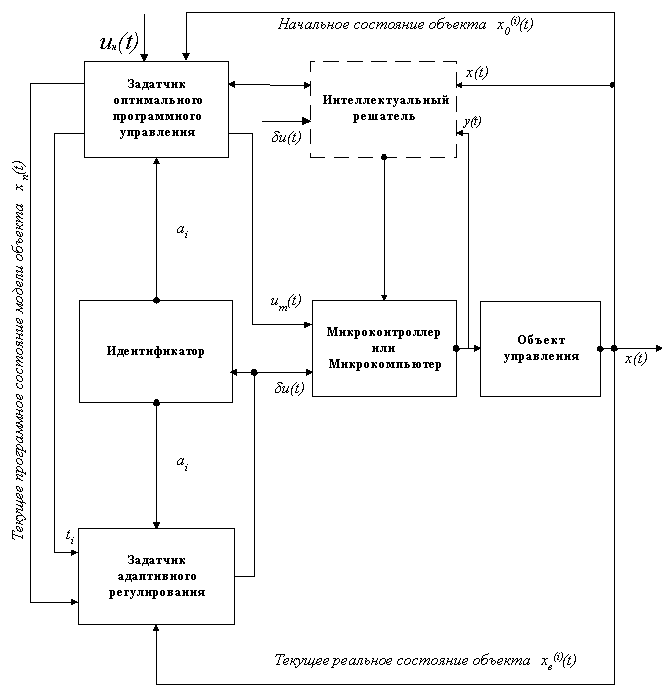
Рис.1 Функциональная схема научно-исследовательского вычислительного комплекса моделирования и автоматизированного проектирования.
Система частных вариаций функционалов
(1) представляет собой систему интегральных
уравнений, которые легко решаются благодаря
тому, что состоят, как правило, из типовых
табличных интегралов. В результате решения
получаем систему уравнений переключения
управления, из которой находятся моменты
переключения 
при
заданных 
и 
.
Модель адаптивного регулирования
Реальное движение системы, как правило, будет отличаться от программного из-за неточности модели объекта, неточной реализации начальных условий и т.п. Поэтому необходимо учесть отклонения реального управления от программного
(2)
(3)
В результате приходим к системе частных вариаций функционала возмущенного движения
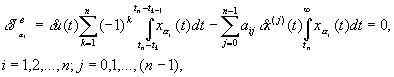(4)
Система уравнений (4) представляет собой модель возмущенного движения, которая используется для проектирования контура адаптивного регулирования с целью обеспечения стабилизирующего движения системы.
Модель активной идентификации
Математическая модель идентификатора строится на основе методов планирования экспериментов и моделей оптимального программного управления и адаптивного регулирования (рис 2).
На данном рисунке показана схема имитации процесса идентификации с применением динамических моделей различных линеаризированных стационарных систем управления в условиях параметрической неопределенности и случайных помех.
Активная идентификация была выполнена с использованием системного интегратора MathConnex программы MathCad.
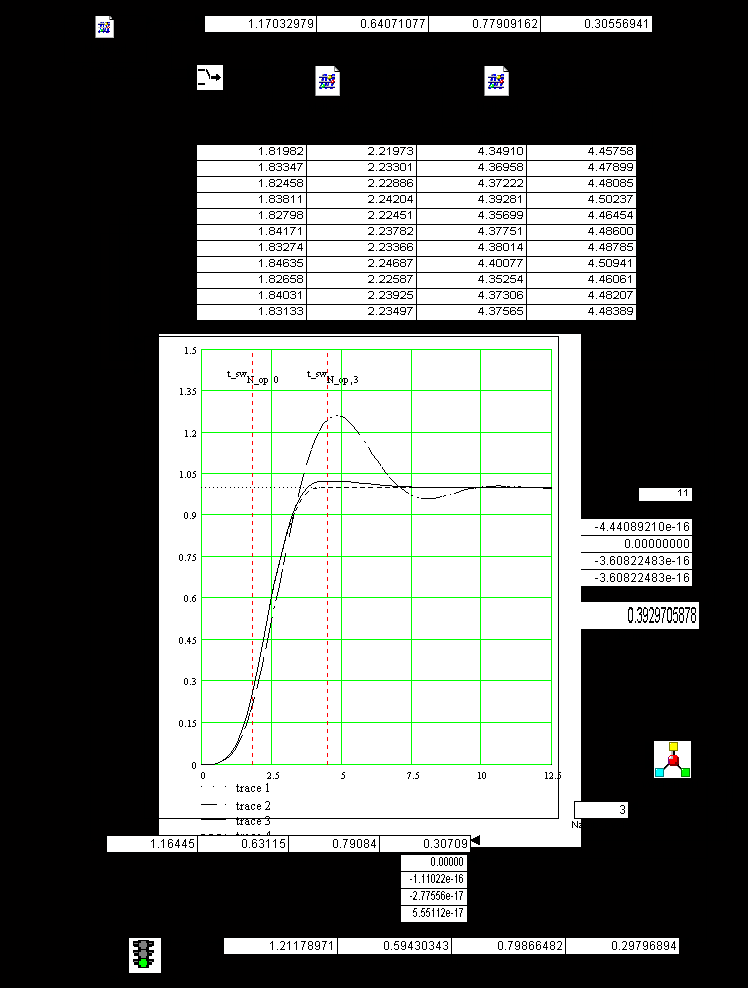Рис. 2. Схема
имитации процесса идентификации с применением
динамических моделей
и отклонения управляемой переменной и ее производных от программного
Литература
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|