 |
||
Mönch, Lars
Germany, Ilmenau, Technische Universität Ilmenau, Institut für Wirtschaftsinformatik,
Lars.Moench@wirtschaft.tu-ilmenau.de
Gmilkowsky, Peter
Germany, Ilmenau, Technische Universität Ilmenau, Institut für Wirtschaftsinformatik,
Peter.Gmilkowsky@wirtschaft.tu-ilmenau.de
PRODUCTION CONTROL OF THE STEPPER EQUIPMENT
IN A SEMICONDUCTOR WAFER
FABRICATION PLANT
Abstract: In this paper we present a concept for the production control of stepper equipment in the photolithography area of a semiconductor wafer fabrication facility. Our concept is based on simulation and heuristic optimization. We describe the conditions of the underlying production process. Then we formulate the corresponding sequencing problem. We develop a suitable objective function and describe the constraints. To solve the sequencing problem we suggest a genetic algorithm.
Резюме: Мы представляем концепцию для контроля продукции стэппэров в области фотолитографии на микроэлектронной фабрике. Наш метод базируетcя на моделировании и эвристической оптимизации. Мы описываем условия процесса производствa. Мы формулируем соответствующую проблему последовательности, развиваем подходящую целевую функцию и описываем ограничительные условия. Для решения проблемы последовательности мы предлагаем генетический алгоритм.
The manufacturing of integrated circuits (IC) on silicon wafers is a complex production process (cp.[1,9]). Between 250-500 process steps on 50-120 different types of equipment are required to produce a medium complexity circuit. Batch processes, expensive equipment and reentrant flows are typical for this type of production. The production of Application Specific Integrated Circuits (ASIC) is additionally characterized by a wide range of product types and the demand to achieve good delivery performance. A product moves through the semiconductor wafer fabrication plant (waferfab) in lots. Each lot consists of several wafers. The photolithography area is a typical example for a bottleneck in a waferfab. The photolithography equipment is very expensive. Every wafer passes through the photolithography area several times because the circuits are made up of layers. Coating, exposure, developing and process control are the main steps of the photolithography process. In a first step the wafer is coated with a thin film of a light sensitive polymer. Then the wafer is exposed by using ultraviolet light. To do this, the light is projected through a mask. The exposure process is finished when all circuits of the wafer have been exposed. The step&repeat equipment for the exposure is called stepper. In this paper we study the problem of stepper scheduling. Problems of this type have been investigated by special consideration of reticle management in [2,5]. Mathematical programming is used for the solution. However, due dates, operators' availability and special constraints for process control are not considered. Simulation experiments for a special photolithography tool are described in [11]. The combination of a genetic algorithm and simulation for the optimization of cluster tools is described in [3].
We model the steppers as parallel machines. Suppose, that n lots queue for processing in front of the steppers. We have to distribute the lots over m steppers. For a single stepper we have to sequence the lots with respect to the following constraints:
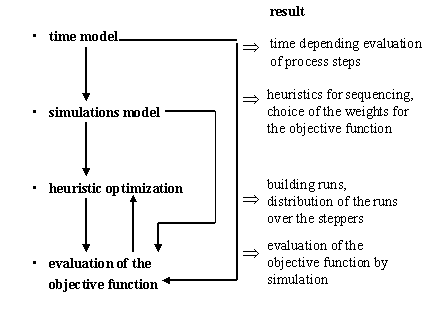
Figure .1 Basic steps of the solution
We denote the set of indices of lots in the queue by ![]() . Let
. Let ![]() be the indices of the runs, which will be completed on the steppers in the
planning period
be the indices of the runs, which will be completed on the steppers in the
planning period ![]() . We denote by
. We denote by ![]() the indices of the corresponding lots. The
endpoint of
the indices of the corresponding lots. The
endpoint of ![]() is
is ![]() . By
. By ![]() we denote the
indices of those runs, which require a send-ahead wafer for process control. Note, that we
distinguish between runs and lots. In fact, we use the run based time model (3.1), but we
have to measure the tardiness for each single lot.
we denote the
indices of those runs, which require a send-ahead wafer for process control. Note, that we
distinguish between runs and lots. In fact, we use the run based time model (3.1), but we
have to measure the tardiness for each single lot.
We denote a distribution of the lot set ![]() over the steppers by
over the steppers by ![]() .
.
We will use the following combined objective function:
(.1) ![]()
with
![]() : full time for
processing run k on a stepper,.
: full time for
processing run k on a stepper,.
![]() ,
,
![]() : finishing time of lot
k on a stepper,
: finishing time of lot
k on a stepper,
![]() : due date of lot k on
a stepper,
: due date of lot k on
a stepper,
![]() : mean time between
starting a send-ahead wafer and processing the successor wafer.
: mean time between
starting a send-ahead wafer and processing the successor wafer.
The first part of the objective function (2.1) measures the throughput
on the steppers, the second term is a penalty term for tardiness, the last part is a
penalty term for send-ahead-wafers. The coefficients ![]() in the objective function (2.1) are weights. The choice of the weights
depends on the desired control strategy.
in the objective function (2.1) are weights. The choice of the weights
depends on the desired control strategy.
We obtain the following optimization problem
subject to the constraints (1), (2) and (3). We show essential steps of the suggested solution in Figure 2.1.
We develop a time model for the time-depending evaluation of process steps on the steppers. The number of steps depends on the product type. The exposure time depends on the product type and on the mask level. Therefore we cannot use the results of [8]. We have derived the following expression for calculating the processing time:
(.1) ![]()
with
![]() : full time for
processing a run on a stepper,
: full time for
processing a run on a stepper,
![]() : time for choosing a
recipe, time for loading a reticle, time for loading and unloading lots on a stepper,
: time for choosing a
recipe, time for loading a reticle, time for loading and unloading lots on a stepper,
![]() : number of wafers in
the run,
: number of wafers in
the run,
![]() : time for loading the
wafer and alignment,
: time for loading the
wafer and alignment,
![]() : number of steps per
wafer,
: number of steps per
wafer,
![]() : exposure time for a
single step,
: exposure time for a
single step,
![]() : time for the
alignment of the stage with the wafer after a step.
: time for the
alignment of the stage with the wafer after a step.
We use the time model (3.1) for mapping the process into a simulation tool. Apart from mask availability we also consider operators’ availability. We incorporate a mechanism for handling send-ahead wafers in our simulation model. First simulation experiments indicate that the strategy for building runs is essential for the quality of the solution. The number of send-ahead wafers is reduced by building runs. The constraint (1) is not so important for ASIC-manufacturing because of the broad range of product types. We can apply the simulation results and expert knowledge to obtain heuristics for solving the optimization problem.
In this section we describe a genetic algorithm to build runs and
to distribute the lots over the steppers. We cannot expect to obtain an optimal solution
with the aid of a genetic algorithm, but it is possible to find near-to-optimal solutions.
For a comprehensive study of the concept of genetic algorithms we refer to [7]. In a first
step we try to find runs in an optimal sense. Therefore we distribute the lots to groups
of the same product type and the same layer. Each element of a group is represented by ![]() . If the group element is 1, a new run will be
started by this lot, otherwise, the corresponding lots are members of the run. We refer to
[6], where a similar method is used to find optimal-sized batches. We obtain for each
element of the population
. If the group element is 1, a new run will be
started by this lot, otherwise, the corresponding lots are members of the run. We refer to
[6], where a similar method is used to find optimal-sized batches. We obtain for each
element of the population ![]() runs as a
result of one iteration of the algorithm. Now, in a second step we distribute the runs
over the steppers by another genetic algorithm (cp.[3] for a similar situation). We use a
list representation for the run set. The list is a permutation of
runs as a
result of one iteration of the algorithm. Now, in a second step we distribute the runs
over the steppers by another genetic algorithm (cp.[3] for a similar situation). We use a
list representation for the run set. The list is a permutation of ![]() . In order to assign runs to the
. In order to assign runs to the ![]() steppers we use an array with entries from
steppers we use an array with entries from ![]() . We use genetic standard operators as
described, for example, in [7]. We consider the objective function (2.1) as the fitness
function for the genetic algorithm. We will use a simple simulation program to evaluate
the fitness function. This program is essentially based on the time model (3.1). We also
have to incorporate the operators’ availability and the mask availability in order to
fulfill the constraints. We will make use of heuristics obtained by expert knowledge and
by simulation in order to build the initial population of the algorithm.
. We use genetic standard operators as
described, for example, in [7]. We consider the objective function (2.1) as the fitness
function for the genetic algorithm. We will use a simple simulation program to evaluate
the fitness function. This program is essentially based on the time model (3.1). We also
have to incorporate the operators’ availability and the mask availability in order to
fulfill the constraints. We will make use of heuristics obtained by expert knowledge and
by simulation in order to build the initial population of the algorithm.
In this paper we present a concept for production control of the stepper equipment in a waferfab. We have described the special production conditions in some detail. Furthermore, we have introduced a suitable time model. The proposed approach for production control uses simulation and heuristic optimization. In the future we will implement the genetic algorithm with the aid of the framework “Galib” (cp. [10]). We expect, that it will be possible to apply some other kind of local search, for example, tabu search within the framework HOTFRAME (cp.[4]), instead of genetic algorithms. However, carrying out the details is part of future research.
[1] Atherton, L.F. and Atherton, R.W.: „Wafer Fabrication: Factory Performance and Analysis“, Kluwer Academic Publishers, Boston, Dordrecht, London, 1995
[2] Carrasco, J., Alptekin, S.E. and Krumme, L.: „Mixed Integer Programming Applied to Stepper Scheduling“, in Proceedings of the 1999 International Conference on Semiconductor Manufacturing Operational Modeling and Simulation, SCS Western Multiconference, San Francisco, CA, January 1999
[3] Dümmler, M.A.: „Using Simulation and Genetic Algorithms to Improve Cluster Tool Performance“, in Proceedings of the 1999 Winter Simulation Conference, 875-879
[4] Fink, A. and Voß, S.: „Generic Metaheuristics Application to Industrial Engineering Problems“, Computers & Industrial Engineering 37 (1999), 281-284
[5] Hickie, M., Fowler, J.W. and Carlyle, W.M.: „Photolithography Reticle Management Through Network Analysis“, in Proceedings of the 1999 International Conference on Semiconductor Manufacturing Operational Modeling and Simulation, SCS Western Multiconference, San Francisco, CA, January 1999
[6] Jordan, C.: „A Two-Phase Genetic Algorithm to Solve Variants of the Batch Sequencing Problem“, Int. J. Prod. Res. 1998, Vol. 36, No.3, 745-760
[7] Michalewicz, Z.: „Genetic Algorithms + Data Structures = Evolution Programs” Springer, Berlin, Heidelberg, New York, Third edition, 1996
[8] Schmalfuß, V., Kämpf, B. and Mönch, G.: „Zeitmodell für die Produktionsplanung
und –steuerung in der Halbleiterfertigung“, ZWF 94 (1999) 10, 601-607
[9] Uzsoy, R., Lee, C.-Y. and Martin-Vega, L.A.: „A Review of Production Planning and Scheduling Models in the Semiconductor Industry, Part I: System Characteristics, Performance Evaluation and Production Planning“, IIE Transactions on Scheduling and Logistics, 24, 1992, 47-61
[10] Wall, M.: „Galib. A C++ Library of Genetic Algorithm Components“, http://lancet.mit.edu/ga/, 1995
[11] White, K.P. and Trybula, W.J.: „Operational Simulation of an EUV Lithography Cell“, in Proceedings of the 1999 International Conference on Semiconductor Manufacturing Operational Modeling and Simulation, SCS Western Multiconference, San Francisco, CA, January 1999
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|