 |
||
Yeremeyev V., Matveyev A., Anufriyeva A.
Latvia, Riga, Transport and Communications Institute,
e-mails: yerem@mailbox.riga.lv, kuzq13@mail.lv
HIGH-PERFORMANCE DIGITAL FILTERING
This paper describes a new method for design of high selective narrow-band lowpass digital filters with exactly linear phase. Synthesized filters have unified structure components and even high order filters provide wide dynamic range of processing data. There is possibility of the passband fast adjustment of the high selective narrow-band lowpass filters, the main advantage of which is not only a miss of transient behavior, but also high computational efficiency.
еремеев В.П., Матвеев А.Г., Ануфриева А.В.
Латвия, Рига, Институт Транспорта и Связи,
e-mails: yerem@mailbox.riga.lv, kuzq13@mail.lv
ВЫСОКОПРОИЗВОДИТЕЛЬНАЯ ЦИФРОВАЯ ФИЛЬТРАЦИЯ
Рассмотрен новый метод проектирования узкополосных фильтров нижних частот (ФНЧ) с линейными фазочастотными характеристиками, имеющих унифицированные структурные компоненты и обеспечивающих при любых порядках широкий динамический диапазон. Предложена методика быстрой перестройки полосы пропускания, позволяющая синтезировать перестраиваемые высокоэффективные ФНЧ.
Обычно важным практическим критерием является объем вычислений, требуемый для выполнения фильтрации, зачастую определяющий принципиальную возможность обработки данных в реальном времени [1]. Независимо от реализации операции умножения требуют наибольших затрат времени и объема оборудования. Иными словами, сокращение вычислений обусловлено в первую очередь степенью минимизации общего числа умножений.
Известная альтернатива – использование рекурсивных структур для уменьшения требуемого числа умножений. Однако коэффициенты, на которые умножаются выборки при рекурсивной высококачественной фильтрации, приходится задавать с очень высокой точностью. Последнее обусловлено тем, что даже небольшая погрешность в значениях коэффициентов может привести к неустойчивости фильтра.
Считается, что фильтры, реализуемые без умножений, практически неосуществимы, поскольку именно умножителями обычно и формируют частотные характеристики. Известные реализации - однородные и триангулярные [1,2] не обеспечивают высокую избирательность и малую неравномерность амплитудно-частотных характеристик (АЧХ) в полосе задерживания. Кроме того, рекурсивная структура по существу неустойчива, а нерекурсивная реализация однородных фильтров высокого порядка крайне избыточна по числу сумматоров [2]. Покажем сначала, что количество сумматоров в однородной структуре (рис. 1) может быть минимизировано.
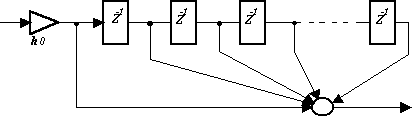
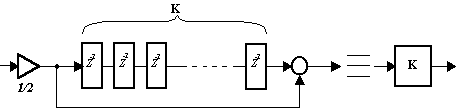
Рисунок 1. Однородная структура. |
Рисунок 2. Универсальное звено. |
Ее передаточную функцию можно представить в виде:
![]()
Если принять N = 2n-1, то при реализации однородного фильтра N–го порядка не потребуется выполнять единственную операцию умножения, так как умножение на 2–n сводится в системах с фиксированной точкой к тривиальным сдвигам разрядов множимого. Уровень наибольшего бокового лепестка таких фильтров составляет примерно 20% от главного. Формулу (1) при N = 2n-1 можно записать иначе:
H(z) = 1/(N+1) · (1+z-1)· (1+z-2)· (1+z-4)· (1+z-8) ... (2)
В этом случае фильтр реализуется каскадной структурой (рис. 3) с минимальным числом сумматоров. Выбор параметров и структуры отдельных блоков очевиден и будет показан ниже.
В частности, при N = 255, классический однородный нерекурсивный фильтр имеет S = 255 сумматоров, в то время как в новой структуре мы имеем всего S = log2(N+1), то есть только 8 сумматоров. Ясно, что теперь скорость обработки данных будет гораздо выше. А поскольку триангулярный фильтр можно представить каскадным соединением двух идентичных однородных – указанная возможность минимизации числа сумматоров и здесь остается в силе. Еще более важным является возможность значительного уменьшения уровня боковых и ширины главного лепестка за счет рациональной интерференции АЧХ в общем случае неидентичных, но унифицированных каскадно включаемых звеньев (рис. 2).
Рассмотрим вначале простой пример N = 15. По предлагаемой ниже методике синтезирован фильтр, представленный на рис. 4, а АЧХ соответствующего однородного и синтезированного фильтров показаны на рис. 5. Таким образом, уровень максимального бокового лепестка снизился с 0.2222 до 0.07655, что соответствует изменению в 2.9 раза.
![]()
![]()
Рисунок 3. Каскадная структура. |
Рисунок 4. Синтезированный фильтр. |
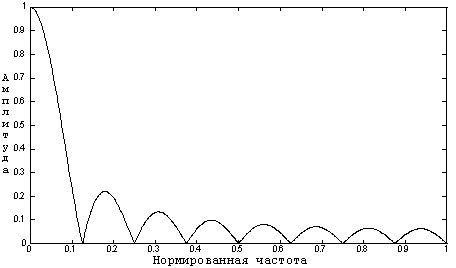
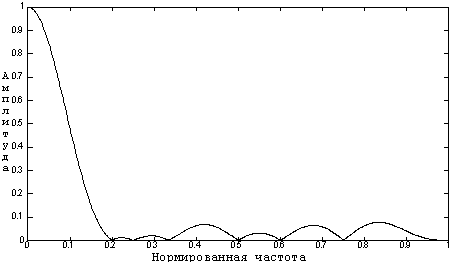
Рис. 5,а. АЧХ однородного фильтра N=15. |
Рис. 5,б. АЧХ синтезированного фильтра. |
Для нахождения параметров табулированных ниже фильтров была составлена программа, осуществляющая отбор фильтров, определяемых разбиениями числа N (порядок фильтра). Фиксировались наборы (паспорт фильтра), обеспечивающие наилучшие передаточные характеристики по двум критериям: минимум максимума передаточной функции в полосе задерживания (для максимального подавления помех) и минимум контрольной частоты (для обеспечения максимальной узкополосности фильтра). С целью уменьшения времени поиска паспорта использовался специальный эвристический алгоритм, так как полный перебор всевозможных комбинаций требует чрезмерных временных затрат. Использована следующая процедура: находятся все разбиения (с возможностью повторения элементов) порядка фильтра N, то есть все последовательности чисел, сумма которых равна N. Полученная последовательность является паспортом фильтра, расчет которого и производится. Перебор завершается после рассмотрения всех возможных разбиений числа N. Если фильтр имеет более качественные показатели по указанным выше критериям - его паспорт и параметры записываются на место наилучшего из фиксированных ранее.
Результатом произведенного исследования является таблица значимых параметров найденных фильтров, состоящая из 1000 вариантов и содержащая фильтры порядков от 15 до 128, краткая выборка из которых приведена в таблице 1.
Таблица 1.
Номер, № |
Порядок фильтра, N |
Паспорт фильтра |
Макс. уровень бокового лепестка |
Норм. граница полосы задерживания |
1 |
64 |
1 1 1 2 3 4 6 8 9 13 16 |
0.0100770 |
0.059339 |
2 |
65 |
1 1 2 2 3 5 6 7 10 12 16 |
0.00911214 |
0.059872 |
3 |
66 |
1 2 2 3 4 6 8 10 13 17 |
0.0103458 |
0.056227 |
4 |
67 |
1 1 2 2 3 4 6 8 10 13 17 |
0.00972134 |
0.056349 |
5 |
68 |
1 2 2 3 4 6 8 10 14 18 |
0.0124752 |
0.052869 |
Для еще более высоких порядков процедура поиска наилучших фильтров требует экспоненциально нарастающих временных затрат. Это связано еще и с тем, что анализ каждой из все более "изрезанных" частотных характеристик требуется выполнять в большем числе точек. Но процедуры поиска можно вообще избежать, используя каскадное соединение полученных фильтров. Практика показывает, что получаемые реализации мало в чем уступают наилучшим. Рассмотрим фильтр порядка N=48, паспорт которого 1 1 1 1 2 3 4 5 5 7 8 10, уровень максимальных пульсаций в полосе задерживания a=0.00320069 и нормированная граничная частота полосы задерживания w s=0.096612. Фильтр данного порядка можно получить путем каскадного соединения нескольких фильтров. Рассмотрим для примера соединение фильтров 21 и 27 порядков с паспортами 1 1 1 2 3 5 8 и 1 1 2 3 4 6 10 соответственно, параметры комбинированного фильтра при этом составляют a=0.00463247 и w s=0.0905.
Выше описанные ФНЧ имеют монотонные в полосе пропускания АЧХ и являются неперестраиваемыми. В ряде приложений необходимы фильтры с возможностью оперативной перестройки полосы пропускания. Предлагается методика реализации перестраиваемых без переходных процессов ФНЧ с конечными импульсными характеристиками (КИХ) высокого порядка, причем перестройка ширины полосы пропускания осуществляется единственным изменяемым умножителем.
Из набора оптимальных неперестраиваемых ФНЧ выбираем два фильтра ФНЧ1 и ФНЧ2 с паспортами P1 и P2, передаточными функциями которых являются H1 и H2, определяющие граничные характеристики, в пределах которых будет осуществляться перестройка, а коэффициент a, изменяющийся в интервале от 0 до 1, определяет положение получающейся характеристики фильтра в пределах этих границ (рис. 6). В частности, при a=0 передаточная функция фильтра равна H2, а при a=1, соответственно, H1.
Для примера возьмем фильтры с паспортами P1 = [1 1 1 2 2 3 5] и P2 = [1 1 1 2 3 4 5 7]. Блок-диаграмма проектируемого фильтра и его АЧХ при некоторых значениях изменяемого коэффициента a представлены на рисунках 8 и 7 соответственно.
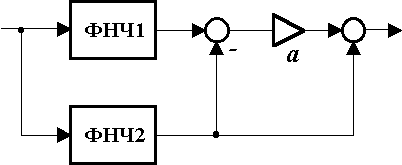
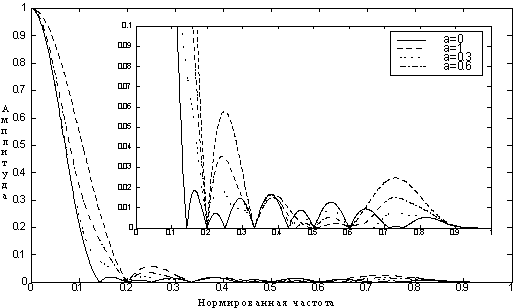
Рис. 6. Общая структура перестраиваемого фильтра. |
Рис. 7. АЧХ синтезированного фильтра. |
Рассмотрим специальный случай, когда оба фильтра содержат одинаковые структурные блоки. Это позволяет сгруппировать такие компоненты впереди и сократить общее количество элементов, необходимых для реализации фильтра, что повышает его вычислительную эффективность. Более того будем рассматривать в дальнейшем только такие пары фильтров, когда один целиком содержит фрагменты другого. Обозначим общую часть (она же является паспортом фильтра меньшего порядка P1) через NI , а дополняющую часть второго фильтра - через NII. Краткая выборка из набора рациональных комбинаций фильтров с хорошими характеристиками в полном диапазоне перестройки приводится в таблице 2.
Таблица 2.
? |
NI |
NII |
Порядок фильтра 1 |
Порядок фильтра 2 |
Уровень максимальной пульсации |
Минимальная полоса при перестройке |
Максимальная полоса при перестройке |
Изменение полосы пропускания |
1 |
1 1 2 3 4 5 8 10 |
1 6 12 |
34 |
53 |
0.0342504 |
0.026113 |
0.035086 |
0.008973 |
2 |
1 2 3 4 5 8 11 |
1 7 13 |
34 |
55 |
0.0423375 |
0.024393 |
0.033529 |
0.009136 |
3 |
1 1 2 3 4 6 8 10 |
1 5 12 |
35 |
53 |
0.0339614 |
0.026113 |
0.034274 |
0.008161 |
4 |
1 1 2 3 4 5 8 11 |
7 13 |
35 |
55 |
0.0398142 |
0.024393 |
0.033465 |
0.009072 |
5 |
1 1 2 2 3 4 4 5 7 8 |
1 1 5 9 |
37 |
53 |
0.00439070 |
0.030452 |
0.038067 |
0.007615 |
Кроме этого, при добавлении определенного числа задержек каскадно в первый фильтр, можно добиться уменьшения уровня боковых лепестков в полосе задерживания при перестройке. Однако, прямое добавление элементов задержки ведет к нежелательному усложнению структуры и уменьшению быстродействия, что можно избежать следующим образом. В начале ветви NII ставится первым унифицированный блок с наибольшим числом элементов задержки, а выход NI снимается с необходимой задержкой уже из этого блока. В частности, выбрав например из таблицы 2 фильтр с порядковым номером 3, получим реализацию, приведенную на рис. 9.

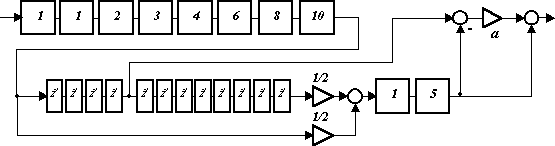
Рис. 8. Реализация синтезированного фильтра. |
Рис. 9. Эффективная реализация фильтра. |
Для рассмотренных фильтров оптимальное количество дополнительных задержек приведено в таблице 3. Отметим, что наилучшее число добавочных элементов задержки в принципе зависит от диапазона перестройки. Для максимального диапазона это число определяется при значениях а, близких к единице.
Таблица 3.
? |
Оптимальное количество дополнительных задержек |
Cнижение наибольшей пульсации (%) при a <= 0.7 |
Снижение наибольшей пульсации (%) при a <= 0.8 |
Снижение наибольшей пульсации (%) при a <= 0.9 |
1 |
9 |
2.7039 |
1.6319 |
0.7229 |
2 |
2 |
0.6158 |
0.3553 |
0.1579 |
3 |
4 |
2.1788 |
1.2632 |
0.5823 |
4 |
4 |
7.3036 |
4.3062 |
1.9350 |
5 |
7 |
1.1323 |
0.6563 |
0.2903 |
При решении практических задач необязательно использовать полный диапазон изменения параметра а от 0 до 1. При заданном диапазоне перестройки, удовлетворяющим условиям конкретной задачи, можно детально исследовать параметры характеристик фильтра в зависимости от числа дополнительно включаемой задержки. Сужение диапазона перестройки часто приводит к существенному уменьшению уровня максимальной пульсации в полосе задерживания. Для рассмотренного примера при изменении коэффициента a от 0.38 до 0.70 оптимальное число дополнительных задержек – 4. Этому соответствует перестройка полосы пропускания в интервале от 0.027664 до 0.030276 и снижение максимального бокового лепестка с уровня 0.0339614 до 0.0235278 (т.е. в 1.44 раза).
Ссылки
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|