 |
||
Truhachev V.V., Spunitis A.A.
Latvia, Riga, Transport and Telecommunication Institute, e-мail: eugene@mail.eunet.lv
DIGITAL FILTERS WITHOUT MULTIPLIERS SYNTHESIS
Abstract. The synthesis of recursive digital filters without multipliers is described in this article. The offered algorithm gives the possibility to decrease the number of adders up to minimum, satisfying the ordered for filter characteristic.
Трухачев В.В., Спунитис А.А.
Латвия, Рига, Институт транспорта и связи, e-мail: eugene@mail.eunet.lv
Синтез цифровых фильтров без умножителей
Аннотация. В статье рассматривается синтез рекурсивных цифровых фильтров без умножителей. Предлагаемый алгоритм сводит количество сумматоров для фильтра заданного порядка до минимума, обусловленного требованиями к его характеристикам.
Один из способов повышения быстродействия и (или) уменьшения шумов цифровых фильтров заключается в замене операции умножения на несколько операций сложения [1-3]. Например, операция 0.74609375 * X может быть выполнена как X*2-1 + X*2-2 – X*2-8, т. е. за два суммирования и 3 сдвига. Поскольку время выполнения операции сдвига намного меньше операции сложения, можно сказать, что умножение в приведенном примере может быть выполнено за 2 сложения. В данной статье приводится метод уменьшения количества сумматоров в цифровых фильтрах без умножителей за счет рационального укорачивания коэффициентов как для задаваемого пользователем начального приближения, так и при совместном решении задач аппроксимации передаточной функции цепи, удовлетворяющей заданным требованиям, и реализации фильтра с минимальным числом сумматоров.
Рациональное укорачивание коэффициентов
Пусть, например, при заданных требованиях к характеристикам фильтра получена аппроксимация его передаточной характеристики в виде каскадного соединения биквадных блоков (и апериодического блока для нечетных порядков)
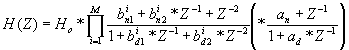
Представим каждый из коэффициентов биквада в базисе:
b = аk1*2k1 + аk2*2k2 + ... +аkn*2kn , (1)
где аki может принимать одно из значений {-1,0,+1}, а ki - целые числа.
Укорачивание коэффициентов заключается в отбрасывании некоторого числа младших элементов разложения (1) при обязательном удовлетворении требований на характеристики фильтров. Возможность такого подхода обуславливается как имеющимся обычно запасом на выполнение требований к характеристикам в силу выбора целого порядка фильтра, так и специально задаваемыми для этой цели более жесткими требованиями (с запасом) к этим характеристикам на этапе аппроксимации H(z).
Иллюстрация 3-х возможных способов укорачивания коэффициентов (по 1, по 2 и по 3 элементам разложения) биквада приведена в табл. 1. Каждой ячейке таблицы соответствует количество сокращаемых младших ненулевых значений элементов коэффициента при представлении его в базисе (1). Так, например, 1 означает отбрасывание последнего слагаемого. Для каждой комбинации укороченных коэффициентов ищется значение целевой функции фильтра и выбирается та комбинация, которая соответствует наилучшему значению целевой функции. Для выбранной комбинации повторяют процедуру сокращения коэффициентов. Так продолжается до тех пор, пока характеристики фильтра вписываются в отведенные коридоры.
Таблица 1
| bn1 | bn2 | bd1 | bd2 | bn1 | bn2 | bd1 | bd2 | bn1 | bn2 | bd1 | bd2 |
| 1 | 2 | 3 | |||||||||
| 1 | 1 | 1 | 1 | 2 | |||||||
| 1 | 2 | 2 | 1 | ||||||||
| 1 | 1 | 1 | 3 | ||||||||
| 1 | 1 | 1 | 2 | ||||||||
| 2 | 1 | 1 | 1 | ||||||||
| 1 | 1 | 1 | 2 | ||||||||
| 1 | 1 | 2 | 1 | ||||||||
| 1 | 1 | 2 | 1 | ||||||||
| 2 | 3 | ||||||||||
| 1 | 2 | ||||||||||
| 1 | 1 | 1 | |||||||||
| 1 | 2 | ||||||||||
| 1 | 1 | 1 | |||||||||
| 1 | 1 | 1 | |||||||||
| 1 | 2 | ||||||||||
| 2 | 1 | ||||||||||
| 2 | 1 | ||||||||||
| 3 |
Для уменьшения числа возможных вариантов перебора коэффициентов биквадов предлагается следующая процедура укорочения коэффициентов:
В качестве примера возьмем низкочастотный эллиптический цифровой фильтр 6-го порядка с нормализованной полосой пропускания до 0.2, с затуханием в ней не более 0.25 дБ (допустимое 0.725 дБ); с полосой подавления от 0.4 и затуханием не менее 75 дБ (допустимое 65 дБ). Следует отметить, что хотя полученный фильтр после процедуры укорочения имеет в полосе затухания 68.81 дБ не следует уменьшать допустимый коридор приемлемых значений передаточной функции фильтра, поскольку в этом случае возможна ситуация, когда на следующем этапе укорочения АЧХ может улучшиться по сравнению с предыдущей итерацией укорочения. Передаточная характеристика этого фильтра в Z-области
![]() , (2)
, (2)
что соответствует 77 сумматорам в случае реализации фильтра без умножителей ( в квадратных скобках указано количество элементов в базисе (1)).
Ниже приведена таблица для шага 1 (последовательное сокращение по одному элементу )
т.е. количество сумматоров уменьшилось до 25.
Таблица для шага 2, N = 9, k = 4 ( сокращение по 13 элементов ) имеет вид
- 21 сумматор.
Фильтр без умножителей будет иметь передаточную характеристику вида:
![]()
![]()
Каноническая биквадная реализация фильтра без умножителей состоит из 21 сумматора и ни одного умножителя, а классическая реализация фильтра с умножителями будет иметь 9 умножителей и 12 сумматоров.
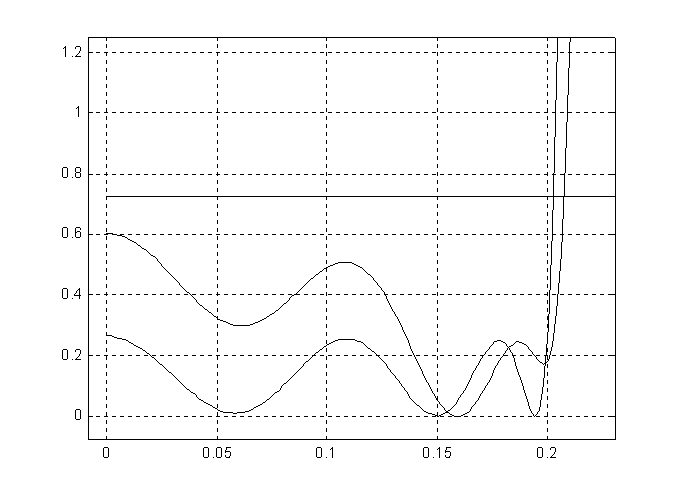
Совместное решение задач аппроксимации и укорачивания коэффициентов
Одним из возможных способов улучшения алгоритма синтеза цифровых фильтров без умножителей является подключение процедуры рационального укорачивания коэффициентов для каждого пройденного локального минимума, удовлетворяющего заданным требованиям на характеристики фильтра, в системах проектирования фильтров с использованием методов квазиглобальной оптимизации [4].
Рассмотрим применение данного подхода, если в качестве начальной точки квазиглобальной оптимизации взят рассмотренный ранее прототип эллиптического фильтра 6-го порядка. В результате оптимизации амплитудно-частотной характеристики фильтра удалось уменьшить количество сумматоров до 19 (применение процедуры укорочения коэффициентов фильтра к прототипу дало 21 сумматор). Всего было пройдено 20 локальных минимумов.
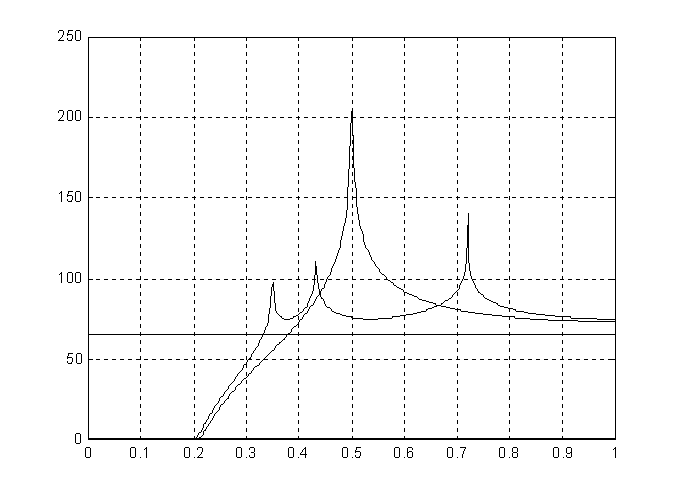
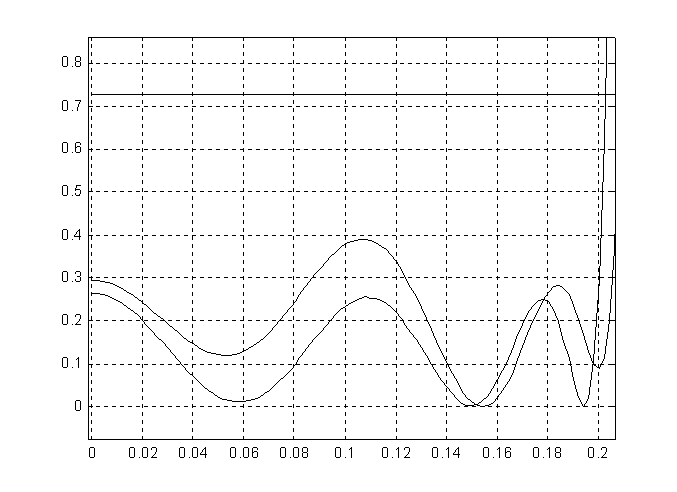
У полученного фильтра 19 сумматоров
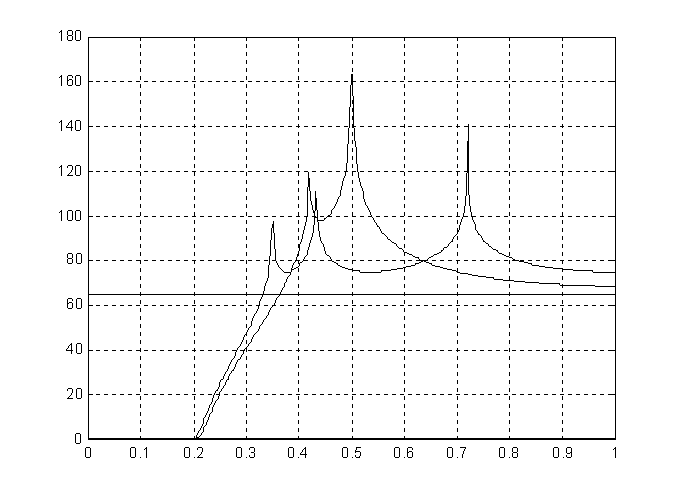
Поскольку укорачивание коэффициентов приводит, как правило, к ухудшению АЧХ фильтра в полосе пропускания, разумно в качестве начального приближения выбирать фильтр требуемого порядка с минимально возможным уровнем неравномерности в полосе пропускания. Этот же подход целесообразен и в случае применения только лишь процедуры укорачивания коэффициентов.
Выберем, например, за исходный вариант эллиптический фильтр шестого порядка с
минимально возможной для заданных требований неравномерностью в полосе 0.002 дБ. Характеристики фильтра после укорачивания коэффициентов имеют вид:
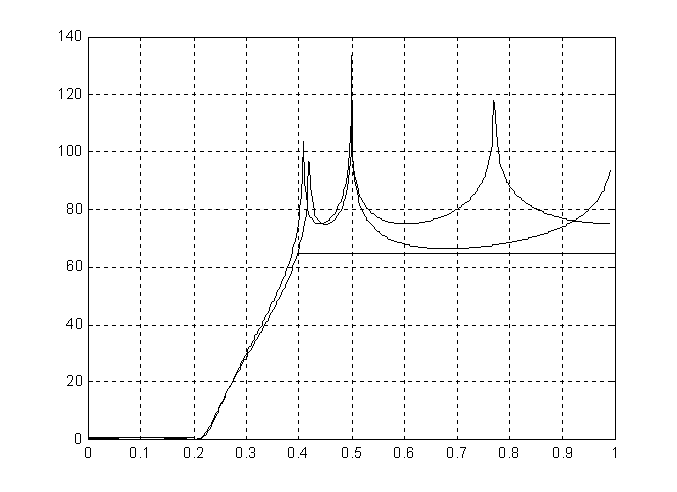
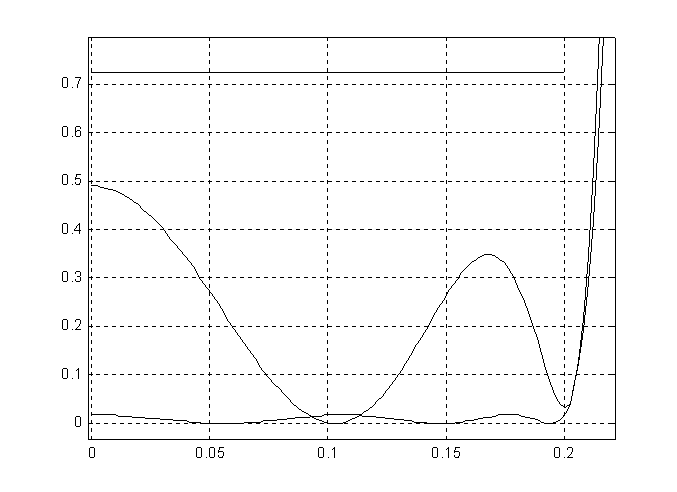
У полученного фильтра 17 сумматоров и коэффициенты при степенях Z-1 в (2) равны
Ниже приведены стандартная реализация цифрового фильтра c умножителями на канонических биквадах, имеющая 12 сумматоров и 12 умножителей,
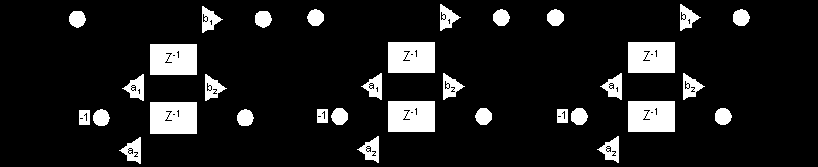
и схема фильтра без умножителей, имеющая 17 сумматоров и ни одного умножителя.
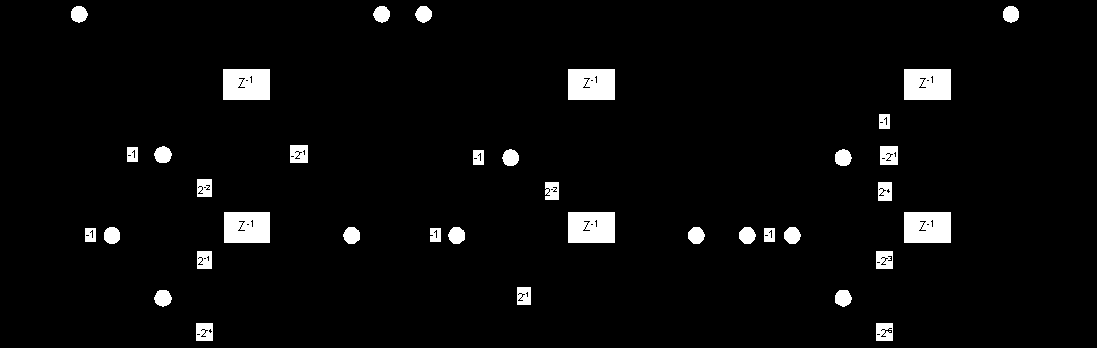
Использование квазиглобальной оптимизации в данном случае не приводит к уменьшению числа сумматоров, что указывает на получение при заданных требованиях цифрового фильтра без умножителей, близкого к оптимальному. В общем случае, при требованиях, заданных не только к АЧХ, но и к иным характеристикам ЦФ, без использования процедуры квазиглобальной оптимизации для совместного решения задач аппроксимации и укорачивания коэффициентов, вероятно, не обойтись.
Литература:
1. Каппелини В., Константинидис А.Дж., Эмилиани П. Цифровые фильтры и их применение. М. Энергоатомиздат. 1983.
2. Мингазин А.Т. Уменьшение разрядности коэффициентов цифровых фильтров введением кратности полюсов и нулей. Известия вузов. Радиоэлектроника. -1987.-12.
3. Kodek D., Steiglitz K. Filter-length word-length tradeoffs in FIR digital filter design. IEEE Trans.; ASSP-28.-1980.-No.6-p.739-744.
4. Трухачёв В.В. Адаптация алгоритма оптимизации многоэкстремальных целевых функций Растригина-Букашкина. Электроника и связь.вып. 2.-Киев. 1998.
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|