Latvia, Riga, Transport and Telecommunications Institute. E-mail: k_andre76@mail.lv

Abstract. Ways of construction of "intelligent" cell (framework) as rectangular parallelepiped with built - in locus are considered. Locus is the intermediary, due to the unique code is put in the conformity which to each specific figure. The reception of information is provided by association of processing of code of figure with management of memory.

Латвия, Рига, Институт транспорта и связи.E-mail: k_andre76@mail.lv

Аннотация. Рассматриваются способы построения ''интеллектуальной'' ячейки (фрейма) в виде прямоугольного параллелепипеда с встроенной извилиной. Извилина является посредником, благодаря которой каждой конкретной фигуре ставится в соответствие свой уникальный код. Рецепция (восприятие) информации обеспечивается объединением обработки кода фигуры с управлением памятью.

Этимологически, фрейм для представления сигналов (от англ. frame – structural skeleton) означает ''интеллектуальную'' ячейку для запоминания и распознавания образца или узнавания стереотипной ситуации. В основе синтезируемых ячеек используется теоретико – категорное представление сигнала [1], суть которого заключается в том, что один математический объект определяется с помощью другого математического объекта.

В прикладных интеллектуальных системах (ПИС) единицей обработки является кадр ( еще одно этимологическое значение для фрейма). Здесь сигнал определяется как геометрический объект, т.е. расположенная в кадре фигура. Более конкретно, это множество точек внутри выпуклой области. В основу построения фреймов в морфологии сигналов кладут открытие Георга Кантора (1877г.), которое состоит в установлении того факта, что мощность множества всех точек квадрата равна мощности всех точек отрезка. Взаимно однозначное соответствие между точками осуществляется с помощью пространственной кривой – извилины.

Задачей синтеза фрейма является выбор извилин (разверток) и построение кода для конкретных графических образов, подлежащих распознаванию.

Конструкция фрейма состоит из прямоугольного параллелепипеда с встроенной извилиной. Извилина – это пространственная кривая, расположенная внутри параллелепипеда, представляющая жестко сочлененную цепь (рис.1). Узловые точки (узлы) извилины – это места соединения звеньев цепи, через которые проходят параллельные основанию плоскости (слои). Между каждым узлом извилины и каждой точкой основания параллелепипеда (кадра) устанавливается взаимно однозначное соответствие. Действительно, если ''шагать'' по плоской кривой, расположенной в основании параллелепипеда, то каждому шагу соответствует построение слоя. Число слоев совпадает с количеством шагов по кривой. Эта плоская кривая называется разверткой. Если по ходу развертка пересекает фигуру, то на соответствующем слое (или в соответствующем узле извилины) устанавливается значение единица; иначе – нуль. В конце хода для бинарного (черно-белого) изображения получаем конечный набор нулей и единиц. Соответствие между извилиной и разверткой приводит к тому, что при смене фигуры в кадре изменится комбинация нулей и единиц в конечном наборе (форма извилины и число узлов не изменяются). Этот набор нулей и единиц имеет смысл только при определенной развертке и фигуре. Другими словами, все элементы структуры (фрейма) взаимосвязаны и не могут рассматриваться отдельно друг от друга. Следовательно, любая подлежащая рецепции фигура в кадре будет однозначно отображаться на заранее построенную извилину. В ПИС фреймы используются как структуры данных для представления образцов или стереотипных ситуаций. Образец принадлежит некоторому классу (например, буквы алфавита, почтовый адрес, элементы некоторых схем, чертежей, фотопортреты, отпечатки пальцев и др.), число элементов которого всегда конечно.

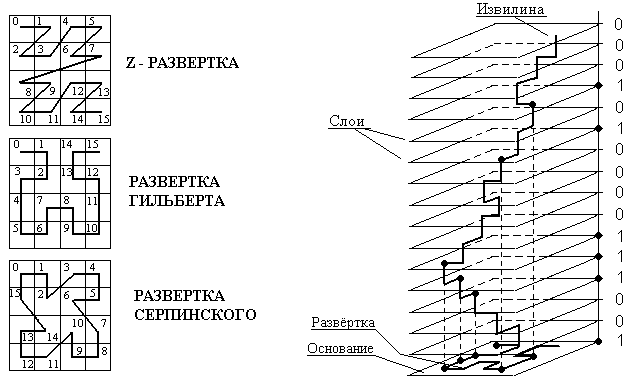
Рис. 1. Пространственная конфигурация на основе одной развертки

В другой интерпретации фрейм это пространственная конфигурация, с помощью которой двумерное изображение можно представить в виде целого числа в двоичной системе. В [2] в качестве способа построения пространственной конфигурации использовались рекурсивные развертки типа кривых Гильберта - Пеано (рис. 1). Рекурсивный подход [3] на основе разверток, сохраняющих двумерные топологические связи, позволяет увеличить сжатие изображений, используя стандартные алгоритмы.

Построение иерархических структур (тетрарных деревьев) оказывается весьма полезным приемом при реализации поэтапной передачи, т. е. использования сжатия изображений в передатчике с постепенным воспроизведением кадра на приемном конце. Такая конфигурация учитывает лишь взаимную связь между близлежащими элементами изображения в восьмиместной окрестности (8-окрестности). Это дает возможность получить выигрыш при сжатии информации. Более результативным фреймом является пространственная конфигурация на основе двух разных разверток (рис.2). При этом одна развертка учитывает ''ближний порядок'', т.е. в 8-окрестности, а другая – ''дальний порядок'' , т.е. взаимосвязь между удаленными участками изображения.

Рис.2. Рекурсивное отображение образца на основе двух разверток

Это составное отображение дает возможность конструировать и использовать разнообразные клики, т.е. системы окрестностей. Для наложения (суперпозиции) двух разверток справедливо следующее утверждение. Если каждая развертка порождает возрастающую последовательность, то их сумма и произведение располагается в счетную возрастающую последовательность попарно различных точек. С каждой конкретной разверткой связано разбиение плоскости на плитки (см. квадратики или прямоугольники на рис.1).Развертка указывает порядок обхода плиток. Множество плиток составляет покрытие кадра. На каждой плитке для всех точек принимается постоянное значение (0 или 1 для бинарного изображения). Наложение двух покрытий будет означать совместное рассмотрение (в смысле теории множеств) попарно различных плиток.

Решение задачи кодирования образца приводит к реализации механизма сопряжения нумераций плиток (или гиперкубов всех разбиений). Заметим, что каждому покрытию кадра плитками соответствует разбиение отрезка в определённом порядке. В [4] показано, что отображения типа кривой Гильберта – Пеано удовлетворяют условию Гельдера и обеспечивают непрерывность однозначного отображения отрезка в гиперкуб.

На рис. 3 в качестве ''образца'' показана точка на соответствующей плитке (конкретный гиперкуб), которая кодируется на отрезке своим “штрих-кодом”. Здесь разбиение и нумерация гиперкубов (плиток) соответствует развертке Гильберта.

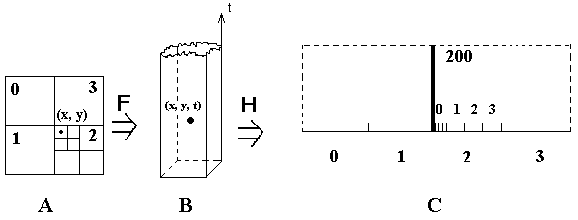
Рис.3. Кодирование образца на основе развертки Гильберта

Информационной точке в квадрате ставится в соответствие узел на извилине (на рис.3 извилина не изображена). Согласно алгоритму сопряжения нумераций, этому узлу ставится в соответствие точка на отрезке, положение которой отмечено “штрихом” или кодом 200. Заметим, что при другой развертке “штрих” будет располагаться в другом месте этого же отрезка. Если образцы представлены множеством точек, то каждому образцу будет соответствовать свой штрих-код. Обоснованием этому утверждению являются теоремы о возможности отображения точек квадрата на отрезок прямой и о разрывности (дискретности) такого отображения.

Практическая полезность представления сигналов фреймами заключается в том, что форма графического образца (паттерна) воспринимается как целостная структура, т.е. без анализа частей. Кадр обрабатывается в “целом”. Рекурсивный подход к представлению изображений обеспечивает реализацию идеи объединения обработки кода фигуры (набора нулей и единиц) с управлением памятью.

1. Александров А.И.,Граковский А.В.,Хейфец Е.М.Морфология сигналов и ее применение // Системы обработки и моделирования сигналов: Тр. научно-техн.семинара СОМ'99, 28 июня…1 июля 1999 г.- Псков,1999.- с.17-22.
2. Александров А. И., Козлов А. М. Представление сигналов фреймами // Системы обработки и моделирования сигналов: Тр. научно-техн.семинара СОМ'99, 28 июня…1 июля 1999 г.- Псков,1999.- с.24-27.
3. Александров В.В., Горский Н.Д. Представление и обработка изображений. Рекурсивный подход. – Л.: Наука, 1985. – 192с.
4. Стронгин Р.Г. Численные методы в многоэкстремальных задачах.-М.:Наука,1978.-240с.