Abstract. The practical realization of the morphologic analysis of radio-location signals and two-dimensional graphic images as the processing of input digital data is presented here. The classification of the dots (samples of signal) takes place in known geometrical figure and singularities of signal construction as locally in the neighborhood of each dot, as globally in the records of signal on final interval.

Аннотация. Представлена практическая реализация морфологического анализа радиолокационных сигналов и двумерных графических изображений как обработка поступающих цифровых данных, при которой происходит классификация отсчетов сигнала в известной геометрической фигуре и особенностей строения как локально в окрестности каждой точки, так и глобально в записи сигнала на конечном интервале.

Альтернативная цифровая обработка сигналов в системах реального времени основана на алгоритмах, использующих теорию особенностей дифференцируемых отображений. При этом исходный сигнал представляется как геометрический объект (многообразие коразмерности 1), а основной метод обработки состоит в сравнении “куска” заданной кривой с другой кривой, строение которой локально известно.

Считается, что особенности формы (очертания, вида, образа сигнала) находятся в прямой зависимости от наблюдаемого явления. Понятия “строение сигнала” и “особенности” его формы означают, что на поверхности - прообразе и на плоскости - образе можно выбрать локальные координаты так, что в этих координатах отображение поверхности на плоскость запишется в виде нормальных форм [1]. Таким образом, запись физического процесса (исходный сигнал) будет состоять из “стандартных кусков” и мест их “склейки”.

Основная идея морфологического анализа сигналов [2] георадара сводится к тому, что вместо формальных уравнений, описывающих деформацию сигнала, используются методы вычислительной геометрии. Аксиома однородности и изотропности пространства утверждает, что совокупность решений уравнения, определяющая распространение возмущения в среде, имеет одну и ту же форму для всех координатных систем, полученных одна из другой переносом и вращением осей. С другой стороны, согласно принципу Кюри, электрическое поле в среде имеет характеристическую симметрию, которая есть подгруппа цилиндричской группы преобразований. Нарушение однородности и изотропности приводит к дисимметрии, т.е. к характерной деформации формы сигнала.

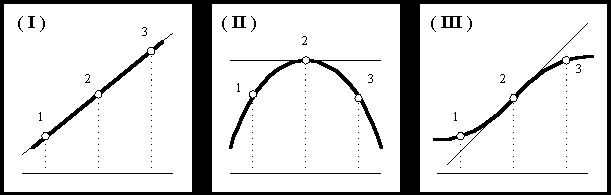
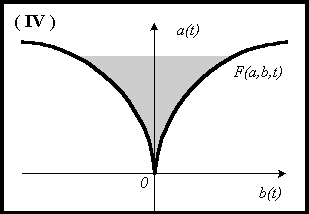
Рис.1. Классификация точек сигнала. Выход точки за границы

заштрихованной области (IV) является признаком цели

Если сигнал – гладкая кривая, то основная задача заключается в классификации характерных точек на кривой, число которых всегда конечно. “Гладкая” означает, что в каждой точке существует производная и, следовательно, можно всегда провести касательную и нормаль в каждой точке этой кривой, т.е. ввести локальную систему координат. Три случая взаимного расположения точек (отсчетов сигнала) относительно локальной системы координат (Рис.1) соответствуют линейной форме (I), квадрике (II) и кубике (III). Других типов точек для сигнала, заданного на конечном интервале, быть не может. Соотношение между числом точек каждого типа будет меняться в зависимости от зондируемой среды, причем с отражениями от радиолокационных целей связывается кубический тип точки. Действительно, согласно принципу Ньютона, сила, деформирующая кривую, пропорциональна второй производной, а этому условию удовлетворяет кубика (Рис.1(III)).

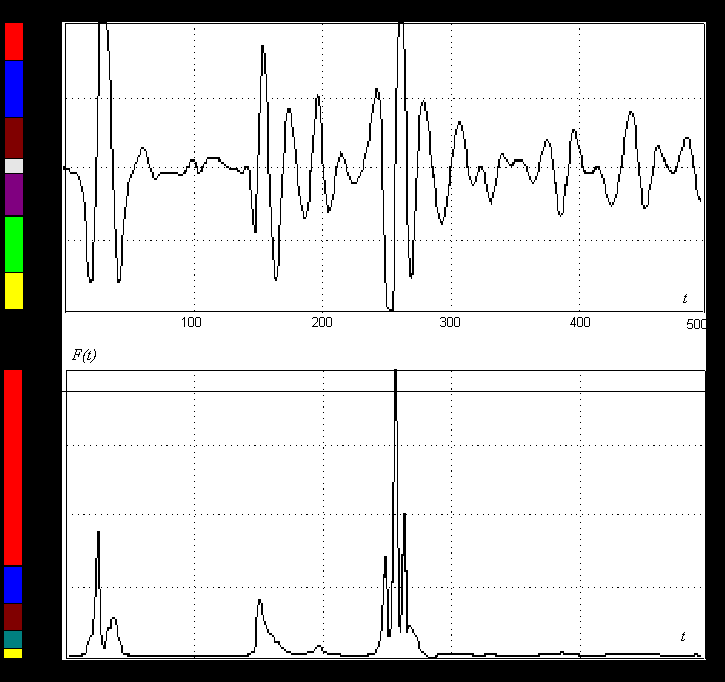
Рис.2. Пример обработки отдельных трасс (реализаций) локационного профиля (см. Рис. 4)

Рассмотрим отображение отдельной реализации зондирующего импульса (Рис.2) на пространственную кривую в виде комплексного аналитического сигнала

где - огибающая, а - мгновенная фаза на интервале одной развертки по длительности . В [2] установлено, что анализируемый процесс описывается при помощи трех параметров: двух внешних

(2)

и одного внутреннего - , а состояния равновесия образуют поверхность

(3)

соответствующего числа измерений. Проекция этой поверхности на плоскость внешних параметров может иметь особенности, связанные с отражениями от целей. Физическая интерпретация особенностей [2] заключается в том, что группа отражений всегда порождает сборку – катастрофу [1] (Рис.1(IV)). Тогда параметры формы описывают функцию с дважды вырожденными особыми точками, позволяющими определять положение целей при подповерхностном зондировании.

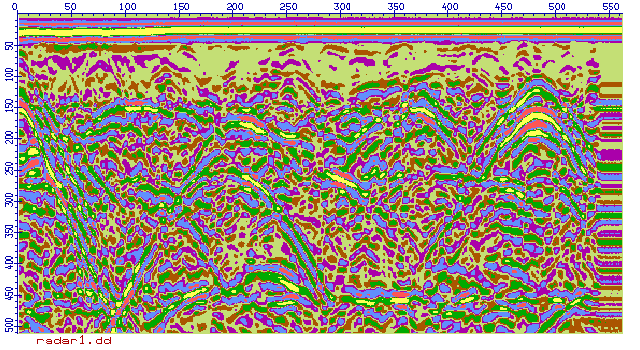
Рис.3. Профиль, построенный по исходным данным георадара (слева)

и по результатам морфологической обработки (справа)

В качестве примера представлены результаты амплитудной регистрации сигналов, полученные в ходе экспериментов по подповерхностному зондированию малоразмерных целей на испытательном полигоне. Реализация сигнала и результат обработки представлены на Рис.2.

Индикация результатов зондирования по исходным сигналам (Рис.3) в значительной мере затруднена сложным характером взаимного наложения радиолокационных профилей отдельных объектов зондирования.

В то же время использование для обработки данных зондирования описанного выше метода (Рис.3) дает возможность непосредственной фиксации во вмещающей среде местоположения зондируемых объектов, что существенно повышает информативность получаемых результатов при решении инженерно-геологических задач с помощью радиолокационной аппаратуры подповерхностного зондирования.

Задача дескрипции (распознавания) двумерных графических образов, в отличие от сигналов георадара, предусматривает использование для морфологического анализа и сравнения фрактальных или “колючих” кривых [4]. При вычерчивании кривой, заполняющей квадрат, возможны только два случая: если кривая развертки пересекает графический образ, то значению переменной присваивается 1, а если нет – то 0. Тогда результат преобразования двумерного изображения есть последовательность нулей и единиц (Рис.4), образующая длинное двоичное число. Это число всегда будет целым. Оно является первичным дескриптором формы, например, в задачах медицинской диагностики или автоматизированном микроскопическом исследовании состава крови.

Рис.4. Преобразование двумерного графического изображения

(рентгеноскопия грудной клетки человека) в двоичное число

Естественно, это число имеет смысл только при определенной развертке (телевизионной, Гильберта, Пеано, Серпинского или др.) [3]. Поэтому в данной задаче важен удачный выбор развертки и построение подходящей арифметики или алгебры для дальнейшего анализа такого отображения. Существенно здесь то, что отображение наследует все свойства исходного образа, т.е. обработка ведется по кадрам.

Преобразование изображения в число зависит не только от формы и размеров фигуры, но и от положения фигуры внутри выпуклой области. Меняя изображение по форме, размерам и положению внутри квадрата, будем получать различные числовые значения для заданного графического изображения.

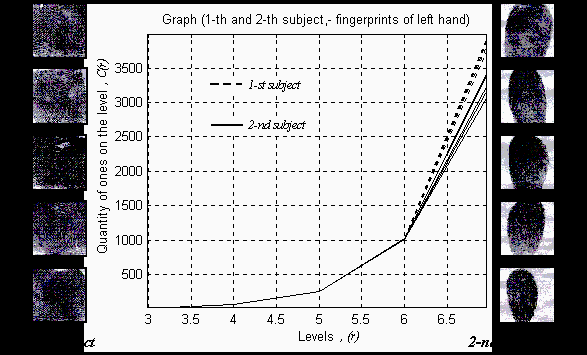
Рис.5. Сравнительный анализ отпечатков пальцев левой руки двух разных людей

По этим данным определяется сигнатура, которая учитывает только признаки, не зависящие от положения и размера объекта. Они связаны с определенной интерпретацией исследуемого объекта.

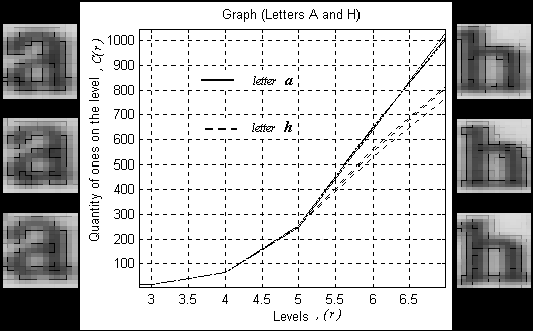
С другой стороны, для анализа и сравнения длинного двоичного числа, в которое отображается графический образ (Рис.4), возможно использовать емкостную меру – фрактальную размерность [5], измеряемую при сканировании графического образа развертками разных порядков. Результаты сравнительного анализа отпечатков разных пальцев левой руки двух разных людей приведены на рис.5. Образы близких по структуре и содержанию объектов (отпечатки пальцев) классифицируются и разделяются при вычислении их фрактальной размерности. Тот же результат получается при сравнительном анализе изображений букв (Рис.6), где несмотря на различия в элементах фона все исследуемые образы классифицируются на две группы.

Рис.6. Сравнительный анализ различных вариантов образов двух букв латинского алфавита

Общим и наиглавнейшим моментом при решении всех этих задач является выбор и построение такого геометрического объекта (или каркаса, или фрейма), при отображении на который исходных данных или сигнала вся искомая информация выделяется в явном виде.

Литература

1. Арнольд В.И., Варченко А.Н., Гусейн-Заде С.М. Особенности дифференцируемых отображений. Классификация критических точек, каустик и волновых фронтов. Т.1,2 - М.: Наука, 1982.
2. Александров А.И., Граковский А.В., Кутев В.А., Строителев В.Г. Цифровая обработка данных георадара на основе анализа структурных особенностей отраженных сигналов. - Сборник научных трудов факультета радиоэлектроники и вычислительных систем.- Рига, РАУ, 1995, с.24-31
3. Александров А.И., Козлов А.М. Представление сигналов фреймами. “Системы обработки и моделирования сигналов СОМ-99”, Труды научно-технического семинара, 28 июня – 1 июля 1999 г., Псков, с. 24-27.
4. Mandelbrot B.B. The Fractal Geometry of Nature. Freeman, New York, 1982.
5. Мун Ф. Хаотические колебания. М. : Мир, 1990.