Russia, Saint-Petersburg, The Saint-Petersburg state university

Abstract. The main aim of this paper is to show probability of group analysis on the easiest level. There are definition of algebraic operation, looking for it's properties and margins on therepresented matrix for each property in the paper for it. Matrix representation can be used for the records of differential equations with analytical right sides in dimentionless form. So it's applied area sufficient in order to include Telemedcine.

Россия, Санкт-Петербург, Санкт-Петербургский государственный университет

Аннотация. Основная преследуемая цель настоящей работы - показать на предельно простом уровне возможности группового анализа. Для достижения поставленной цели соответствующим образом вводится алгебраическая операция, рассматриваются её основные свойства и выясняются ограничения, накладываемые ими на структуру матрицы, представляющей первый сомножитель. Матричное представление позволяет записывать правые части дифференциальных уравнений с аналитическими правыми частями в безразмерной форме. Таким образом область применения развиваемых методов достаточно широкая, чтобы включать в себя и вопросы, связанные с Телемедециной.

There are a lot of calculus defined on the vectors of multidimensional spaces. Put the A[x](y) as a multiplier x· y by two 2D or 3D vectors x and y, where A[x] - a number of set of matrixes

Mnn with a fixed structure. May be n=2 or n=3.

The first question which is attract our attention is next: what kind of structure of A[x] may be in such case:

1) associative;

2) commutative;

3) conversionative;

4) existing of unit element;

5) existing of inverted element.

But At first, we must know what are these in mathematics language.

The associative is property: (x· y)· z=x· (y· z). We have got two expressions for each side of the latest equation:

(x· y)· z = A[(x· y)](z) = A[A[x](y)](z)

and

x· (y· z) = A[x](A[y](z)) = (A[x]A[y])(z).

The result is next: A[A[x](y)]=A[x]A[y]. In general case A[x]A[y] is matrix A[Z(x, y)], where Z(x,y) - the form by the components of two vectors - x and y.

The commutative is property: x· y=y· x. In another words A[x](y)=A[y](x), which in case of associative of operation is mean that commutator

[A[x], A[y]] = A[x]A[y]-A[y]A[x] = 0.

The group unit is defined as the element e which is: A[e]=E. For the2D vectors it is equivalent solvability of the next equations: A1x=e1 and A2x=e2. It is true (for the 2D spaces). And we’ve got one expression which links A1 and A2: A1=TA1, where T - a matrix: TT = -E [ e2 = Te1 ]. Promise that the elements of A[x] - the linear forms of components of vector x, i.e.

A[x] = [A1 x, A2 x],

where

A1 =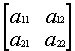 , A2 = .

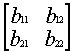Then

A[x] = x1[A1[1],A2[1]] + x2[A1[2],A2[2]] = x1B1 + x2B2 ,

and

A[x](y) = x1y1A1[1] + x1y2A2[1] + x2y1A1[2] + x2y2A2[2] .

Therefore the commutative is equivalent by A2[1]=A1[2]. We have:

(1) A[A[x](y)] = x1y1(a11B+a21B2)+x1y2(b11B1+b21B2)+x2y1(a12B1+a22B2)+x2y2(b12B1+b22B2).

(2) A[x]A[y] = (x1B1+x2B2)(y1B1+y2B2) = x1y1B1B1+x1y2B1B2+x2y1B2B1+x2y2B2B2.

In summary there are four properties of components of matrix A[x]:

a11B1+a21B2 = B1B1,

b11B1+b21B2 = B1B2,

a12B1+a22B2 = B2B1,

b12B1+b22B22 = B2B2.

Matrixes representation of algebraically structures can by apply to modelling processes of control in several path. For example we can write polynomial right side of differential equations as a multiplier with some operations.