A.V.Solomonov, V.I.Zubkov

E-mail: zubkov@fvleff.etu.spb.ru

Deep level transient spectroscopy (DLTS) is widely used in the last 20 years to characterise impurities and defects with deep levels in forbidden energy gap of semiconductors. Its specific features are extremely high sensiti vity (up to 10¹² electrons/cm³) and relative simplicity of hardware.

Unfortunately, there is no often one - to - one mathematical correspondence between the distribution of deep levels in forbidden energy gap of semiconductor and DLTS - spectrum; in a number of cases (semiconductor alloys, for example) it is possible to propose a lot of essentially different solutions, which match the measured spectrum within the bounds of experimental noise. Therefore methods of fitting by several parameters [1], used in modern measuring information DLTS - systems and based on subjective propositions, need some preliminary information about the object under treatment [2,3] and can lead to unstable results. Moreover, sometimes because of the quite broad apparatus function of DLTS - spectrometer one can not determine h ow many deep centers have formed the spectrum observed, and, thus, how many fitting parameters are needed.

We have proposed the algorithm of correct interpretation of complicated DLTS - spectra of semiconductor solid solutions. The algorithm is based on the method of Tikhonov regularization and allows to avoid the subjectivity in determinat ion of deep centers characteristics.

In general the temperature-dependent DLTS spectrum in semi-conductor alloy may be described

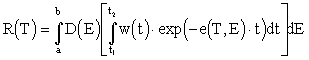, (1)

as where D(E) is the deep center density of states function (DSF) to be found, e(T,E) is the deep center thermal emission rate, w(t) is the weighting function of the DLTS - spectrometer, and (t₁, t2) is the rate window of the spectrometer. One can consider (1) as Fredholm equation of the first kind with the expression in the square brackets as the kernel of the equation.

The solution of the Fredholm equation concerning the function D(E) on the obtained DLTS spectrum is unstable because of the experimental noise. We will solve it with the help of Tikhonov's regularization of ill-posed inverse problems [ 4]. According to it one should minimise the square of deviation of the calculated spectrum from the experimental one using the certain stabilising corrections

,

Obviously, among all existing solutions the most stable solution is the one that is most smooth. So we will find the approximate (regularized) solution D(E) as the most smooth of all solutions matching given error of the experimentally measured R(T). As a smoothness measure of the virtual approximate decisions it is possible to accept the value of a functional W :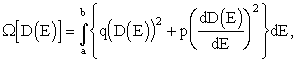

where q and p are non - negative numbers (we have restricted the conditions with a demand of a continuity of the first order derivative).

To get the minimum of the functional Ma it is necessary to equate its first variation to zero:

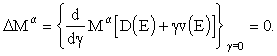
Thus, the problem of obtaining of a stable solution of (1) is reduced to finding of the extremal of the Euler's integro - differential equation:

(2)

The parameter of regularization a , in accordance with the discrepancy principle [5], is determined by the equality of the discrepancies of the experimental and simulated spectra.

For practical computation we made a discretization of Euler equation (2) on an uniform mesh energy-temperature in the region [a < E_i < b; c < T_i < d].

As a result we have got a set of linear algebraic equations:

,

where B_a is the quadratic and symmetrical matrix with a positive determinant; C is a three - diagonal matrix.

The resulting set of linear equations was solved by square root method [4] with the task dimension of 512*512 points.

The suggested algorithm has been used successfully for the resolution of two neighbouring deep centers, having the density of states function of an arbitrary form. Thе solving of this proble m is very important for the interpretation of DLTS data.