 |
||
ГЕНЕТИЧЕСКИЙ ПОДХОД К ОПТИМИЗАЦИИ ВХОДНОГО СИГНАЛА ДИНАМИЧЕСКОЙ СИСТЕМЫ
Л.А Мироновский, К.Ю. Петрова
Санкт-Петербургский государственный университет аэрокосмического приборостроения
Abstract — This paper proposes genetic and combined algorithms for evaluation of operator norms of dynamic systems and the corresponding optimal input signals. These algorithms are compared with each other, with von-Mizes iterative procedure and with method of steepest descent.
Постановка задачи
В ряде прикладных областей (Теория управления, идентификация, метрология, техническая диагностика) возникают задачи определения формы входного сигнала, приводящего к максимальному отклику на выходе системы. Далее предполагается, что входной сигнал ограничен по амплитуде
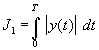
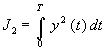 . Тем самым речь
идет об отыскании входных сигналов
. Тем самым речь
идет об отыскании входных сигналовДетерминированные алгоритмы
Можно выделить три подхода к отысканию оптимальных сигналов: а) прямой поиск; б) итерационный подход; в) генетический подход.
Ниже дается краткое описание соответствующих алгоритмов и приводится их сравнение с точки зрения вычислительной сложности, надежности полученных результатов и области применения.
Процедура прямого поиска состоит в следующем. Сначала вычисляется значение критерия J
1 или J2 для постоянного входного сигналаСуть итерационного подхода, предложенного в [1], иллюстрируется рис.1. Согласно нему отыскание оптимального сигнала производится с помощью структурной схемы, содержащей исходную S и сопряженную S* динамические системы, а также одно или два звена с релейной характеристикой. При произвольном выборе начальной функции форма входных сигналов, получаемых на последующих итерациях, сходятся к оптимальной в смысле критерия J
1 (рис. 1, а) или J2 (рис. 1, б).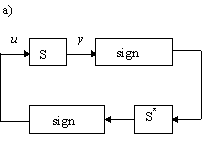

Рис. 1. Итерационный принцип получения оптимальных сигналов
К сожалению, при неудачном выборе начальной функции итерационный алгоритм не гарантирован от зацикливания, поэтому при его использовании нужно перебирать несколько инициализирующих функций.
Генетические алгоритмы
Рассматриваемая задача относится к числу многоэкстремальных задач, не имеющих однозначного решения. Для того чтобы избежать недостатков детерминированных алгоритмов, был исследован генетический подход [2]. В его рамках были разработаны чисто генетический и гибридный алгоритмы. Программная реализация алгоритмов выполнена в системе Matlab 5.2 и Simulink. Такой выбор был обусловлен наличием в пакете мощных возможностей по моделированию динамических систем, а также наличием необходимых возможностей для программирования и отладки.
Благодаря специфике задачи, при построении чисто генетического алгоритма из его структуры удалось исключить шаги кодирования и декодирования. В качестве хромосомы было взято естественное представление релейного управляющего сигнала (сигнатурной
функции) в виде массива, состоящего из чисел 1 и –1, равного по длине дискретному вектору времени (рис 2,а). Операции кроссовера и мутации получили при этом прозрачную физическую интерпретацию. Были использованы одноточечный кроссовер (рис 2, б) и две разновидности двухточечного кроссовера (рис 2, в, г).
|
|
|
|
Рис. 2. Интерпретация хромосомы (а), одноточечного (б) и двухточечных (в, г) кроссоверов
Мутация интерпретировалась как сдвиг отдельной точки переключения (рис.1,а), либо всей функции сразу вправо или влево на случайное количество позиций.
Алгоритм был опробован на небольших временных интервалах, когда количество точек переключения было невелико (одна, две) и можно было бы получить достоверный результат другими методами. Использование чисто генетического алгоритма оказалось малоэффективным, поэтому был разработан гибридный алгоритм, включающий элементы прямого поиска. В целях экономии вычислительных ресурсов процедура прямого поиска в этом алгоритме применяется только к лучшим особям, т.е. особям, доставляющим максимальную норму выходного сигнала. На каждой итерации проводится проверка, изменились ли сигнатурные функции, доставляющие максимум критерия. Если это так, то запускается описанная процедура "тонкой подстройки" и вносятся соответствующие коррективы в массив флагов, который хранит данные о том, к каким особям уже была применена эта процедура.
При выборе параметров гибридного алгоритма требовалось решить следующие вопросы:
Выбор типа кроссовера (пункт 2) не оказал существенного влияния на работу алгоритма. Наиболее существенными для работы алгоритма оказались пункты 3 и 4.
В качестве возможных процедур инициализации (п. 3) рассматривалась генерация сигнатурных функций следующего типа:
При выборе родителей (п.4) для размножения были опробованы следующие стратегии:
Наихудшим по эффективности оказался второй вариант, а наилучшим– третий.
В алгоритме отсева (п. 5) использовались три различные процедуры:
На каждой итерации отсеивалось от 5 до 15% популяции, либо поддерживалась постоянная популяция.
Для предотвращения зацикливания (п.7) при длительном отсутствии прогресса (если значение критерия не улучшается в течение трех последовательных итераций) задействовался механизм, подобный макромутации: в популяцию добавлялись новые особи, в соответствии с тем же алгоритмом инициализации, который использовался при запуске алгоритма. При этом алгоритм предусматривает у новых особей большее число точек переключения.
Сопоставление алгоритмов
Правильность работы алгоритмов была проверена на задаче Булгакова, для которой известен вид оптимального сигнала – сигнатура весовой функции, развернутой во времени.
Самой трудоемкой операцией в описываемых алгоритмах является моделирование реакции динамической системы на входной сигнал, поэтому их сложность оценивалась именно с точки зрения количества обращений к функциям MATLAB lsim или sim, без учета остальных затрат.
Эксперименты показали, что для относительно небольших интервалов времени, на которых оптимальный входной сигнал имеет небольшое число точек переключения, целесообразно применять алгоритм прямого поиска, либо итерационный алгоритм. На больших временных интервалах лучшим оказался гибридный алгоритм.
Пример
Проиллюстрируем свойства гибридного алгоритма на примере системы, заданной передаточной функцией четвертого порядка
![]()
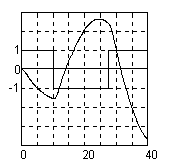
На рис. 3 приведены графики выходных сигналов, полученных с использованием итерационного и гибридного алгоритмов. С помощью итерационного алгоритма был получен входной сигнал с двумя точками переключений и значением критерия
а
)
б
)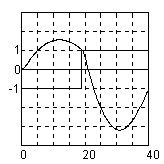
Рис.3. Сравнение результатов итерационного и гибридного алгоритмов.
Гибридный алгоритм нашел входной сигнал с одной ТП и значением критерия
Сходимость гибридного алгоритма для первых десяти поколений и вычислительные затраты, измеряемые количеством операций lsim для той же задачи при Т = 100с. показаны в таблице.
Сходимость гибридного алгоритма
Таблица 1.
Поколение |
1 |
3 |
5 |
7 |
9 |
10 |
||||||
Значение критерия |
264.8 |
265.8 |
268.7 |
269.0 |
269.1 |
269.1 |
||||||
Число операций |
193 |
456 |
587 |
731 |
862 |
921 |
||||||
Заключение
Разработанный гибридный алгоритм требует значительно больших вычислительных затрат, чем метод прямого поиска или итерационный метод, но обладает большей надежностью и универсальностью. Его применение оправдано при большой длине интервала, когда оптимальная функция имеет большое число переключений, которое трудно оценить заранее, а также при рассмотрении нелинейных динамических систем. Универсальность гибридного алгоритма обеспечивается благодаря заложенным в него средствам случайного поиска, а точность получаемых результатов – благодаря механизму "тонкой подстройки".
Литература
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|