Сайт Информационных Технологий

Решение многокритериальных задач оптимизации и принятия решений в нечеткой постановке

Н.П. Деменков

МГТУ им.Н.Э.Баумана, тел./факс: (095) 263-67-27/ 433-64-35.

E-mail: demenkov@ics.bmstu.ru.

Abstract – The decision of multicriteria optimization tasks and decision making in indistinct statement. The article is devoted to consideration of an opportunity of the decision non-formalizable general multicriteria optimization task by the analytic hierarchy process (AHP). The general problem of optimization is understood as a problem with indistinctly expressed criteria and alternatives.

При решении ряда практически важных задач возникают ситуации, когда либо отсутствуют необходимые датчики первичной информации, либо существующие средства измерений не обеспечивают получение требуемой информации в темпе с процессом, либо в наличии имеется лишь качественная информация об объекте управления. В таких ситуациях необходимо иметь информационные технологии, которые позволяют на основе компьютерной обработки качественной или нечеткой информации об объекте и целях управления получить требуемую информацию для управления.

Рассмотрим задачу многокритериальной оптимизации в постановке, когда цели, альтернативы (действия) и исходы заданы нечетко, но для которой отношения предпочтения, т.е. функция полезности, заданы четко.

Для решения поставленной задачи оптимизации нужно определить и максимизировать функцию полезности рассматриваемых альтернатив:

  1. max{U( z1, z2 , . . ., zk )},

где zi = fi(xО S) , i= 1 . . . k, - составлящие вектора критериев, S - множество допустимых решений.

Основной трудностью, возникающей при решении поставленной задачи, является проблема получения математического описания функции полезности U[1]. В теории полезности функция полезности U рассматривается и рассчитывается как вероятностная величина, однако, для многих сложных неформализованных задач принятия решений оценить многомерное распределение вероятности очень сложно и даже неразрешимо.

В данной работе функция полезности рассматривается не как вероятностная, а как нечеткая величина, причем функции принадлежности нечетких множеств рассматриваются как субъективные измерения лиц, принимающих решения (ЛПР).

Многокритериальную задачу оптимизации можно представить в виде иерархической декомпозиции (рис.1), где множество целей обозначено G, а множество альтернатив - X.

Если цели представляются слишком сложными понятиями, их можно представить в виде иерархии более простых понятий.

Элементы иерархии, т.е. цели и альтернативы, являются нечеткими множествами, обозначаемыми на рисунке Gj , j=1. . .m, где m - количество целей и Xr, где r = 1, . . .,l , l - количество альтернатив.

Метод анализа иерархий (МАИ), являясь методом решения многокритериальных задач в сложной обстановке с иерархическими структурами, включающими неформализованные элементы[2], используется в работе как косвенный метод определения функций принадлежности нечетких множеств [3].

Пусть требуется определить функцию принадлежности m D(x) нечеткого множества D’, определяющего некоторое качественное понятие. Для этого ЛПР предлагается сравнить количественные элементы универсального множества X между собой по степени их соответствия этому качественному понятию и заполнить матрицу попарных сравнений A={aij}, элементы которой aij являются оценками степени принадлежности элементов ai О X нечеткому множеству D’ по сравнению с элементами aj О X . Функция принадлежности находится как собственный вектор w матрицы A, соответствующий ее максимальному собственному значению l max

A*w = l max*w .

При анализе сложных свойств, представляемых в виде иерархической системы, описанный подход используется при сравнении составляющих свойства на степень соответствия этому сложному свойству. Для иерархического случая Т.Саати доказана следующая теорема [2]:

Теорема. Пусть H - полная иерархия с элементом b на верхнем 0-м уровне и h уровнями. Пусть Bn - матрица приоритетов n-го уровня, n =1,...,h. Если W’- вектор приоритетов p-го уровня относительно некоторого элемента z в (p-1)-м уровне, то вектор приоритетов W q-го уровня (p<q) относительно z определяется как

(2 ) W= Bq* Bq-1. . .Bp+1* W’.

Таким образом, вектор приоритетов самого нижнего уровня относительно элемента b определяется следующим выражением

(3 ) W = Bh* Bh-1. . . B2* W’.

Решение (2) не может считаться решением задачи (1), т.е. полученное ранжирование не может рассматриваться как функция полезности. Кроме того, технические задачи, требующие формализации качественных характеристик физических величин, не могут решаться методом анализа иерархий в его классической постановке.

Докажем справедливость данной теоремы для случая, когда не вся иерархия рассматривается как нечеткое множество с его универсальным множеством на нижнем уровне, а нечеткими множествами являются элементы иерархии.

Функцию полезности альтернатив можно рассматривать как функцию принадлежности глобальной цели на множестве альтернатив, причем функция принадлежности рассматривается как субъективная, а не как вероятностная величина. Функции принадлежности нечетких множеств, формализующих каждый критерий (сложный, представляемый в виде иерархии или простой) определяются на множестве альтернатив, при этом множество альтернатив является базовым для нечетких множеств критериев. На каждом уровне мы имеем различные четкие упорядоченные множества, которые состоят из элементов, являющихся нечеткими (качественными) и определяются каждый своей функцией принадлежности. Элементы каждого уровня являются нечеткими подмножествами четкого упорядоченного множества и определяются именно в этом смысле.

Пусть иерархия является совокупностью уровней Ln, n=1,...,h.

Любой n-й уровень иерархии является совокупностью отдельных элементов lkj , где j=1,. . .,m, m-количество элементов данного уровня.

Набор элементов lnj является “нечеткими свойствами” для элементов нижнего n+1-го уровня, т.е. lnj - это набор нечетких множеств, универсальными множествами этих нечетких множеств являются множества элементов нижних уровней.

Распишем элементы каждого уровня

Уровень L n-1 : l 1n-1 l2n-1 l3n-1 . . . lm( n-1)n-1

Уровень L n : l 1n l2n l3n . . . lm( n)n

Уровень L n+1 : l 1n+1 l2n+1 l3n+1 . . . lm( n+1)n+1.

Связь соседних уровней иерархии определяется матрицей собственных векторов, т.е матрицей приоритетов B

 

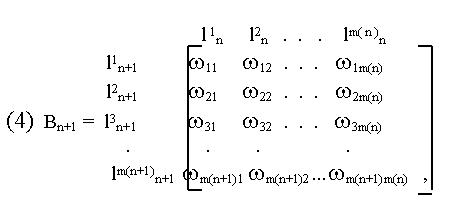
где Bn+1 - матрица собственных векторов уровня Ln+1, m(n+1) - число элементов уровня n+1, m(n) - число элементов уровня n.

Степень принадлежности элемента нечеткому множеству, являющемуся элементом

(5) = w 11 = .

Функция принадлежности нечеткого множества, являющегося элементом l 1n+1,

(6) = [ w 11 w 12 w 13 . . . w 1 m(n) ] т

- функция принадлежности 1-го элемента n+1 уровня, определенная на базовом множестве уровня L n (строка матрицы) .

Функция принадлежности нечеткого множества, являющегося элементом l1n,

(7) =[w 11 w 21 w 31 . . . w m(n+1)1] т

- функция принадлежности 1-го элемента n-го уровня, определенная на базовом множестве уровня L n+1 (столбец) .

Очевидно, что матрица Bn+1 задает бинарное нечеткое отношение между нечеткими множествами, принадлежащих уровням n и n+1

(8) Bn+1є Rn+1, n : L n+1° L n ® [0, 1].

Задача анализа иерархий сводится к нахождению (Ln+1), т.е. к нахождению функции принадлежности нечеткого множества элемента 1-го уровня иерархии, определяемого на базовом множестве уровня n+1. Считаем, что уровень L1 состоит из одного элемента и в иерархии n+1 уровней.

Необходимо найти отношение между нечетким множеством l1 верхнего уровня и нечеткими множествами, принадлежащими уровню Ln+1

(9) R (L n+1, L 1) : L n+1 ° L 1 ® [0,1].

Bn+1 есть матрица нечетких отношений нечетких множеств уровней Ln и Ln+1

(10) Bn+1 =R(Ln+1 , Ln).

Функция принадлежности (Ln+1) определяется как композиция нечетких отношений следующим образом

(11) R(Ln-1)=(Ln+1)=R(Ln+1,Ln)° (Ln).

Иначе эту композицию можно записать следующим образом

(12) (Ln+1) =,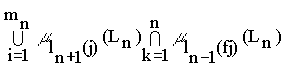

где i= 1...mn - количество элементов n-го уровня, j=1....mn+1-количество элементов n+1-го уровня.

Эта запись эквивалентна выражению (2).

Следовательно, доказана справедливость рассмотрения глобального вектора приоритетов альтернатив (вектора приоритетов) последнего уровня как функции принадлежности глобальной цели решения задачи, которая, в свою очередь, может рассматриваться как функция полезности при решении многокритериальных задач в нечеткой постановке.

Данное утверждение позволяет применять МАИ для решения таких многокритериальных задач, как оценка нечетких моделей сложных систем, где требуется формализация качественных значений физических величин на количественных шкалах.

Таким образом, МАИ может эффективно использоваться не только для принятия решений в неформализованных сферах и решения задач ранжирования конечного множества сложных объектов, представленных в виде иерархической структуры, но и для принятия решений в технических задачах, где требуется формализация всех нечетких понятий с помощью нечетких множеств [4,5]. Это открывает дополнительные возможности для внедрения новых информационных технологий, например, для замены операторов при управления технологическими процессами, улучшения качества управления, позволит строить интеллектуальные системы, способные принимать решения и адекватно реагировать на изменения ситуации на основе знаний человека.

Разработаны методика и программное обеспечение для разработки модели нечеткого логического регулятора (НЛР) для управления сложными техническими объектами, у которых основная часть информации, необходимая для построения модели, является качественной или нечеткой. Информация представлена в виде правил, выраженных на качественном языке естественных понятий и называемых лингвистическими правилами управления (ЛПУ).

В качестве импликации используется операция минимума, если правило формулируется в виде если-то, или операция максимума, если используется правило если-иначе. В качестве правила вывода используется композиционное правило, при котором композиция рассчитывается как максиминная.

Для выбора четкого значения функции управления применяется метод весов, по которому в качестве единственного значения для управления выбирается значение, имеющее максимальную функцию принадлежности.

Модель получения управления, т.е. модель регулятора, представлена в виде иерархической структуры, элементами которой являются влияющие на процесс входные лингвистические переменные, лингвистические правила управления, в которых задействованы эти переменные, и качественные значения этих лингвистических переменных.

Методика позволяет оценить значимость входных ЛП, важность и достоверность ЛПУ, поэтому разработанный НЛР вырабатывает управляющее воздействие с учетом различных параметров и действует адекватно текущей ситуации.

Литература

  1. Штойер Р. Многокритериальная оптимизация. Теория, расчет и приложения. Пер. с англ. М.: Радио и связь, 1992.
  2. Т. Саати, Принятие решений. Метод анализа иерархий. Пер. с англ. -М.: Радио и связь,1993.
  3. Заде Л. Понятие лингвистической переменной и его применение к принятию приближенных решений. М.: Мир, 1976.
  4. Грунина Г.С., Деменков Н.П., Пакет программ, реализующий метод анализа иерархий, Приборы и системы управления, 1996, №6.
  5. Грунина Г.С., Деменков Н.П., Программный комплекс для проектирования нечеткого логического регулятора, Приборы и системы управления, 1997, №8.
Site of Information Technologies
Designed by  inftech@webservis.ru.