Сайт Информационных Технологий

НЕЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ В УСЛОВИЯХ ИНТЕРВАЛЬНОЙ НЕОПРЕДЕЛЕННОСТИ

В.И. Левин

Пензенский технологический институт

Abstract – The problem of Nonlinear Programming with interval Coefficients is presented. Solution of the problem, based on the comparison of interval Numbers, is given.

Известно множество работ по нелинейному программированию (оптимизации) в условиях точно известных параметров оптимизируемой системы. Однако на практике параметры систем обычно известны неточно и заданы, скажем, в форме интервалов. В статье изложены результаты, которые обобщают основополагающие положения нелинейной условной оптимизации (включая выпуклое программирование) на интервальный случай.

Общая задача нелинейного интервального программирования имеет вид

(1)

где - вектор, а функции цели и ограничений - интервальные

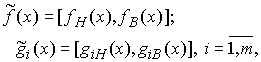(2)

с нелинейными детерминированными нижними и верхними граничными функциями. Для решения задач надо уметь сравнивать интервальные значения ее целевой функции при различных аргументах x и выбирать максимальное (минимальное) значения. Сравнение интервалов выполним согласно правилу [1]: сдвинутый вправо (влево) интервал - больший (меньший), совпадающие интервалы равны, накрывающие друг друга интервалы несравнимы. На основе этого положения доказывается следующая базовая теорема.

Теорема 1. Для того чтобы интервальная функция принимала максимальное (минимальное) значение в точке x* ее допустимой области, необходимо и достаточно, чтобы в этой точке принимали максимальное (минимальное) значения ее нижняя и верхняя граничные функции.

Теорема 1 позволяет сводить интервальные задачи нелинейного математического программирования к двум обычным задачам. Для этого введем две детерминированные задачи нелинейного программирования: нижнюю граничную задачу

(3)

и верхнюю граничную задачу

.(4)

Теорема 2. Для того чтобы интервальная задача нелинейного программирования (1),(2) имела решение x* , необходимо и достаточно, чтобы это же решение имели ее нижняя и верхняя граничные задачи (3),(4).

Теорема 2 сводит решение интервальной задачи нелинейного программирования к решению ее нижней и верхней граничных задач.

Рассмотрим теперь общую выпуклую задачу нелинейного программирования

(5)

-вектор с интервальными функциями цели и ограничений

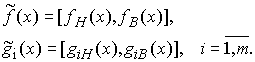(6)

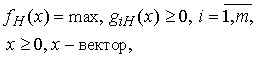В этой задаче по определению все граничные функции вогнутые,а сравнение интервалов выполняется уже упомянутому выше правилу [1]. Пусть А и В - две детерминированные задачи нелинейного выпуклого программирования одинаковой размерности с регулярной допустимой областью. Назовем функцию Лагранжа этих задач согласованными, если они имеют хотя бы одну пару согласованных седловых точек вида c одинаковой первой компонентной . Введем для задачи (5),(6) две детерминированные выпуклые задачи нелинейного программирования: нижнюю граничную

(7)

и верхнюю граничную

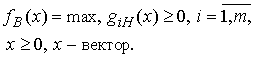(8)

Теорема 1. Для того, чтобы выпуклая интервальная задача нелинейного программирования (1),(2) с регулярной областью допустимых решений граничных задач (3),(4) имела решение , необходимо и достаточно, чтобы ее нижняя и верхняя граничные задачи имели согласованные функции Лагранжа, с согласованной парой седловых точек вида .

Теорема 1 сводит решение выпуклой интервальной задачи нелинейного программирования к отысканию седловых точек функций Лагранжа ее нижней и верхней граничных задач.

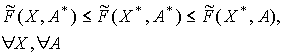Введем интервальную функцию Лагранжа задачи (1),(2) в виде где нижняя (верхняя) граница интервала есть функция Лагранжа нижней (верхней) граничной задачи. Определим седловую точку (X*,A*) интервальной функции Лагранжа в виде

(9)

Теорема 2. В выпуклой интервальной задаче нелинейного программирования (5),(6) с регулярной областью допустимых решений граничных задач (3),(4) точка является решением тогда и только тогда, когда существует точка , такая, что (Х*,А*) - седловая точка интервальной функции Лагранжа задачи.

Теорема 2 имеет для выпуклых интервальных задач нелинейного программирования такое же фундаментальное значение, как и теорема Куна-Таккера для детерминированных задач нелинейного программирования: позволяет свести оптимальную задачу с ограничениями к задаче без ограничений.

Литература

1. Левин В.И. Дискретная оптимизация в условиях интервальной неопределенности // Автоматика и телемеханика 1992.№7.

2. Левин В.И. Нелинейная оптимизация в условиях интервальной неопределенности //Кибернетика и системный анализ. 1999. № 2.

Site of Information Technologies
Designed by  inftech@webservis.ru.