Сайт Информационных Технологий

ОРГАНИЗАЦИЯ И ИСПОЛЬЗОВАНИЕ ГИБРИДНЫХ ЭКСПЕРТНЫХ СИСТЕМ ПОДДЕРЖКИ ПРИНЯТИЯ РЕШЕНИЙ В УСЛОВИЯХ НЕОПРЕДЕЛЕННОСТИ

о. и. шеховцов1, б. м. шифрин2

1СПбГЭТУ “ЛЭТИ”, 2ЛТА

Abstract. The main topic of the paper is an investigation of decision making procedure under condition of uncertainty of information by using hybrid expert systems. The special attention is drawn to the following questions: choice of a model for representing and combining the fuzzy numbers; estimation of the belief degree and prior information impact on accuracy of the obtained results; development of a model for the preference decision maker system and of an algorithm for choice on its basis the optimality criterion.

Основной темой статьи является подход к проектированию современных интеллектуальных средств поддержки принятия управленческих решений.

Многофункциональность разрабатываемых систем обработки интеллектуальной информации может быть обеспечена за счет современного подхода к хранению и использованию знаний проектировщиков [1]. Основной принцип данного подхода заключается в том, что задачи решаются на основе не просто данных, а знаний. Последние являются существенно более мощными и позволяют решать на их основе сложные задачи.

Традиционные экспертные системы (ЭС) имеют лишь один механизм поддержки принятия решений – логический вывод, и лишь одно средство представления знаний – правила. В последнее время активно развивается новое поколение ЭС – гибридные экспертные системы (ГЭС). Для использования ГЭС в качестве средства поддержки принятия управленческих решений необходимо предусмотреть возможность учета характеристик лица, принимающего решения (ЛПР). Предлагается не использовать в системе единую жесткую схему логического вывода, а поддержку принятия решений осуществлять в соответствии с конкретной аналитической моделью пользователя.

При реализации подобных систем наиболее существенными являются следующие проблемы.

1. Экспертные знания, а также информация, которой оперирует ЛПР в процессе принятия решения, часто носят нечеткий характер. Поэтому при проектировании современных интеллектуальных систем необходимо выбрать модель для представления и комбинирования нечетких величин.

2. Разумеется, качество процесса принятия решения зависит от степени доверия к экспертной информации. Необходимо связать достоверность получаемых результатов со степенью доверия к исходной информации.

3. Так как использование ГЭС предусматривает возможность использования предпочтений ЛПР, необходимо разработать модель для анализа и настройки на характеристики конкретного пользователя.

4. Выходом аналитической модели системы предпочтений ЛПР является решающее правило, согласно которому происходит определение наилучшего варианта действий. Для этого необходимо использовать алгоритмы сопоставления предпочтениям ЛПР, в общем случае нечетко определенным, критерия оптимальности.

Для разрешения первой проблемы необходимо выбрать способ представления нечеткой величины.

Нечеткий интервал S можно определить следующим образом [2]:

,

где [,] – ядро; и – нижнее и верхнее модальные значения нечеткого интервала S; l – неубывающая функция, удовлетворяющая условию l-1(1) = ; r – невозрастающая функция, удовлетворяющая условию r-1(1) = ; l-1(1) - l-1(0) = a , где a - левый коэффициент нечеткости; r-1(0) - r-1(1) = b , где b - правый коэффициент нечеткости.

На основании подобного представления возможно обрабатывать нечеткие оценки на основе использования обратных функций, что позволяет в ряде случаев получать результаты в аналитическом виде:

,

, где *О {+, -, Ч , /},

В частности, для наиболее часто использующихся при принятии решений операций сложения и умножения, получаем:

,

.

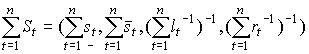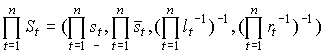Рассмотрим вторую проблему. Перед использованием ЛПР экспертной информации ее необходимо откорректировать в зависимости от уровня противоречивости источника этой информации. Чем выше уровень противоречивости, тем меньше можно доверять экспертной оценке, поэтому ее расплывчатость должна возрастать по мере увеличения противоречивости. Очевидно, если непротиворечивость максимальна (равна единице), то оценка не должна изменяться, а если минимальна (равна нулю) – оценка должна быть полностью неопределенной, одинаковой на всем базовом множестве. Необходимо найти такое преобразование исходной функции принадлежности в зависимости от функции принадлежности ее истинности , чтобы оно адекватно отражало зависимость оценки от степени доверия к ней. Можно использовать следующее преобразование [3]:

.

Третья проблема связана с формализацией предпочтений ЛПР в услових неопределенности. Для этого предлагается использовать двухуровневую модель системы предпочтений ЛПР [4], адаптированную к условиям неопределенности [5]. На верхнем уровне модель представляется совокупностью структурных и функциональных характеристик, где структурные характеристики определяют возможность и условия использования математической модели для описания предпочтений ЛПР, а функциональные характеристики определяют конкретный вид и оценки параметров аналитической модели. К структурным характеристикам отнесены полнота, устойчивость и непротиворечивость. К качестве функциональных используются следующие характеристики: предпочтения на множестве критериев; зависимость критериев; способность оценки объектов по всему множеству критериев или только по частным критериям; способ оценивания элементов задачи принятия решений. Особое внимание уделено непротиворечивости, так как, в основном, именно она определяет способность исследуемого субъекта выступать в качестве эксперта, т.е. его уровень компетентности в данной предметной области. В [5] использовались понятия внешней и внутренней непротиворечивости, где под внешней непротиворечивостью подразумевалась степень соответствия субъективных оценок объектов, данных ЛПР, их достоверным оценкам, а под внутренней непротиворечивостью – степень выполнения основных свойств отношений предпочтения. Нижним уровнем системы предпочтений ЛПР является аналитическая модель.

Для разрешения наиболее существенной четвертой проблемы, связанной с разработкой аналитической модели предпочтений ЛПР, необходимо сопоставить предпочтениям ЛПР, в общем случае нечетко определенным, критерии оптимальности. Разработанный алгоритм выглядит следующим образом.

Исходными данными для алгоритма являются решающие правила , выражающие различные стратегии поведения ЛПР, и априорные полезности альтернатив . В данной постановке можно считать аналогом “обучающей выборки”, относительно которой ЛПР может сформулировать свои предпочтения с тем, чтобы впоследствии обобщить их на все множество объектов [6, 7]. В результате работы алгоритма необходимо получить номер оптимального решающего правила .

1. Оценки полезностей частных критериев для альтернатив , ), подставляются в :

.

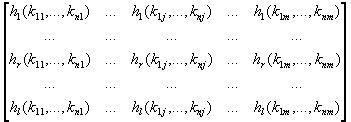2. Имея информационные гранулы: <Априорная полезность j-ой альтернативы равна ,<Полезность j-ой альтернативы по -ой свертке равна > можно получить - степень доверия к оценке j-ой альтернативы по -ой свертке.

3. - степень доверия к -ой свертке.

4. .

Успешное разрешение четырех изложенных проблем позволяет разрабатывать современные интеллектуальные средства поддержки принятия управленческих решений в условиях неопределенности информации, позволяющие учитывать экспертные характеристики и предпочтения ЛПР.

Литература

  1. Интеллектуальные системы принятия проектных решений / А. В. Алексеев, А. Н. Борисов, Э. Р. Вилюмс и др. Рига: Зинатне, 1997.
  2. Дюбуа Д., Прад А. Теория возможностей. Приложения к представлению знаний в информатике. М.: Радио и связь, 1990.
  3. Батыршин И.З. К анализу предпочтений в системах принятия решений // Тр. МЭИ. М., 1981. Вып. 533. Вопросы оптимизации больших систем.
  4. Шеховцов О.И., Клюкин А.И. Деловые игры в автоматизированном проектировании АСУ: Учеб. пособие / ЛЭТИ, Л., 1983.
  5. Шифрин Б.М. Исследование и разработка моделей и средств поддержки принятия организационных решений в нечетком аспекте: Дис…. канд. техн. наук / СПбГЭТУ. СПб, 1999.
  6. Шеховцов О. И., Шифрин Б. М. Прогнозирование состояний объектов на основе методов классификации в нечетком аспекте // Cб. тр. ХV Международной межвузовской школы-семинара. Йошкар-Ола, МарГУ, 1998 г. С. 10-14.
  7. Шеховцов О. И., Шифрин Б. М. Метод классификации на основе нечетких множеств // Управление, информатика и вычислительная техника. СПб, 1998 г. С. 68-71. (Изв. СПбГЭТУ “ЛЭТИ”. Вып. 1).
Site of Information Technologies
Designed by  inftech@webservis.ru.