 |
||
Хаотическое поведение в простой модели управления общим банковским капиталом
R. Mosdorf, J. Nazarko, N. Siemieniuk
Bысшая Школа Финансов и Управления в
Белостоке, Польша
Кафедра Прикладной Информатики
Abstract – Money markets are subject of many analysis and investigations all over the world. They are supported by different methods and research tools. One of the newest concepts of money market description is theory of chaos. This is an attempt to more versatile view of mechanisms governing them. The specific features of markets – unbalance states and feedback mechanism in time dimension – find their expression in description by means of dynamic non-linear systems. The paper presents a simple conceptual model of total banking capital. The simulation calculations were made for two different strategies of total banking capital management. It was shown that apparently simple rules of banking system performance can lead to a very complicated money market behaviour.
1. Введение
Рыночная экономика основана на механизмах и институтах, гарантирующих свободное передвижение капитала. Условием ее развития является четко действующая банковская система. В современной экономике, характеризирующейся разделением труда, обмен продуктами между субъектами производится посредством денег. Для успешного снабжения субъектов средствами платежа, а также правильного функционирования денежного обращения, нужны финансовые посредники. Финансовые посредники это такие институты, главной целью которых является уравновешивание спроса на финансовые вложения одних субъектов с заявленными другими субъектами потребностями в использовании денежных средств. Это осуществляется посредством приема финансовых средств от субъектов, имеющих их излишки, и предоставления их затем в качестве кредитов в распоряжение субъектов, характеризирующихся временным дефицитом средств. Здесь можно говорить о так называемой сделочной функции банков. Кроме этого банки выполняют трансформационную функцию, которая сводится к трансформации размера средств, трансформации сроков, трансформации риска, а также трансформации пространственной алокации средств и трансформации информации [ 1] . С макроэкономической точки зрения банки выполняют роль финансовых посредников, предоставляя в распоряжение услуги связанные с приемом и предоставлением капитала и соединяя таким образом предложение и спрос на капиталовложения.
Во всем мире денежные рынки являются предметом многочисленных анализ и исследований. В них используются различные методы и исследовательские инструменты. Одной с новейших концепций описания рынков является теория хаоса. Это попытка более универсального видения механизмов управляющих денежными рынками. Характерные черты – состояния неравновесия а также механизм возвратного сопряжения во временном измерении – находят свое отражение в описании при помощи динамических нелинейных систем.
В работе [ 4] разработана простая модель симуляции управления общим капиталом банков с использованием теории детерминистического хаоса [ 5, 6] . Показано, что простые с виду правила функционирования банковской системы могут привести к очень сложному поведению банковского рынка.
2. Управление общим капиталом банков
Рациональное функционирование банка детерминировано такой величиной капитала, которая уравновешивает предоставленные кредиты. Это осуществляется посредством определенных принципов управления общим банковским капиталом.
В экономике, находящейся в процессе перемен, принципы свободного рынка сосуществуют с оставшимися от прежнего периода принципами центрального управления экономикой. В случае если вводимые принципы свободного рынка являются нестабильными, управляющие прибегают к принципам центрального управления (в работе называемым целенаправленным управлением), что можно наблюдать в некоторых послекоммунистических странах.
В работе [
4] предложена следующая система уравнений к моделированию изменений общего капитала банка:![]() для
для ![]() (1)
(1)
![]() для
для ![]()
а также
где:
n – очередное рассматриваемое (фиксированное) время,
cn – величина общего капитала банка в период n,
cM, cm – соответственно максимальная и минимальная величина общего капитала банка,
cz – желательная (заданная) величина общего капитала банка,
?, ? –
соответственно коэффициенты динамики падения и увеличения общего капитала банка, зависящие в частности от норм процента.Система уравнений описывает ситуацию, в которой начисление процентов на капитал и кредиты переменно так, чтобы величина общего банковского капитала колебалась вокруг величины
cz. В работе [ 6] к моделированию величины капитала в банке, использующем принцип самоограничивающегося начисления процентов, использовано следующее логистическое уравнение (2):![]()
где: r описывает динамику общего капитала банка
Сценарий возникновения хаоса в уравнении (1) такой же, как в логистическом уравнении (2), к которому можно относиться как к описывающему поведение общего банковского капитала в том случае, когда правление банком модифицирует нормы процента кредитов и вложений таким образом, чтобы величина общего капитала колебалась около
cz. На рисунке 1 показаны примерные изменения очередных итераций уравнения (1) и логистического уравнения (2).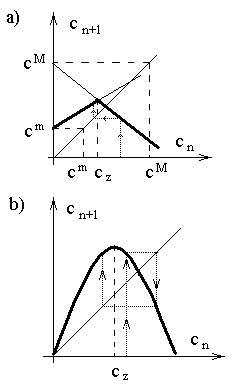
Рис. 1. Примерные изменения итераций:
(а) уравнения (1); (b ) логистического
уравнения (2)
Временной ряд, производимый отображением (2), получается через вычерчивание соответствующей параболы и генерируя очередные точки, начиная с некоторой начальной величины.
В представленной работе проанализирован был анализирован случай, когда правление банка использует две стратегии. Одну агрессивную, характеризирующуюся коэффициентом r
(1), и другой, менее агрессивной, характеризирующуюся коэффициентом r (2). Принимается, что правление банка выбирает более агрессивную стратегию, когда сn упадет ниже величины сz. Когда же величина сn возрастет выше сz, тогда правление банка принимает менее агрессивную стратегию управления общим банковским капиталом. В анализированном случае r(1) > r(2). Уравнение, описывающее изменение общего капитала банка принимает вид:![]()
(3)
![]()
Уравнение (3) является адаптацией метода воздействия фракталов, предложенного в работе [2].
График уравнения (3) показывает рис. 2. В зависимости от последующих значений величины с происходит переход на разные параболы, соответствующие двум значениям коэффициента
r.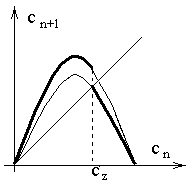
Рис. 2. Изменение итерации функции, описанной уравнением (3)
На рисунке 3 представлены итерации логистического отображения (3). Картина постоянных точек итерации в функции с для принятых значений
r(1) и r(2) показана на рисунке 3(a). На рис. 3(b ) показаны изменения коэффициента Ляпунова в процессе смешивания двух схем итерации.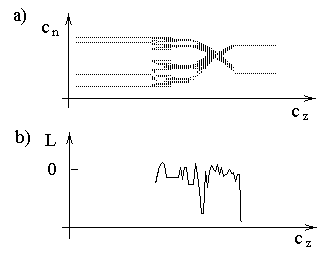
Рис. 3. Итерация логистического отображения (3)
:Положительные значения коэффициента Ляпунова свидетельствуют о чувствительности системы к исходным условиям, т.е. указывают на хаотический характер изменений для некоторых заданных значений величины общего капитала банка.
Результаты вычислений показывают, что две периодических схемы итерации (характеризирующие разные стратегии) создают хаотические итерации
Характеристики промежуточного пространства видны на графике вероятности появления отдельных схем итерации в функции начальной величины вложения сбережений
c (рис. 4).Шкала под рисунком позволяет определить вероятность появления расстановки, которая реализуется для c
n? cz. Это вероятность использования правлением банка второй, менее агрессивной стратегии управления общим капиталом банка.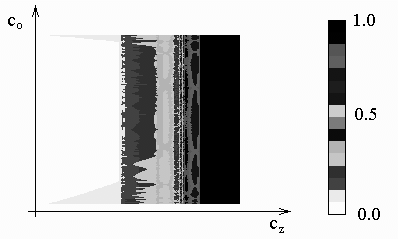
Рис. 4. Картина вероятности появления второго отображения в уравнении (3).
3. Итоги
Предлагаемая модель симулирует изменения общего банковского капитала, которые происходят в экономике, находящейся в процессе трансформации.
Предложенные в работе уравнения, описывающие поведение банковского рынка, а также управляющих, очень просты, поэтому к этой модели надо относиться как к качественной модели.
Итоги симуляционного эксперимента показывают, что банк, вместе с происходящими в нем процессами, может для некоторых описывающих их параметров, проявлять черты характерные для хаотических поведений.
Полученный результат показывает, что даже очень простая схема функционирования экономики в период трансформации может привести к очень сложным поведениям банковского рынка. Это значит, что классические стратегии управления во многих случаях должны быть пересмотрены.
Фрактальный анализ может являться полезным инструментом, позволяющим оценивать вероятность определенных поведений на рынке, а также моделировать альтернативные сценарии его развития.
Литература
1. Buschgen H. E., Przedsiebiorstwo bankowe, Poltex, Warszawa 1997.
2.
Janeczko S., Jastrzebski P., On interaction of classical fractals, Preprint IMPW 1996.3. Levy H., Sarnat M. Capital investment and financial decisions, Prentice Hall, NY 1990.
4. Mosdorf R., Siemieniuk N., Modelowanie wybranych aspektow zarzadzania kapitalem calkowitym banku z zastosowaniem teorii chaosu
deterministycznego. Miedzynarodowa konferencja naukowa nt. Zmiany w systemie finansowym w latach 90-ych na przykladzie wybranych krajow Europy. Wyzsza Szkola Finansow i Zarzadzania, Bialystok 20-21 maja 1999.5. Peters E. E., Chaos and Order in the Capital Markets. A New View of Cycle. Prices and Market Volatility, New York 1996.
6. Shuster H. G., Determinic Chaos: An Introduction. VCH, Weinheim 1989.
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|