1. Введение

В настоящее время можно выделить два основных подхода к теории систем (греч. s u s t h m a - состав). Первый - эмпирический подход основан на анализе и математическом моделировании эмпирических взаимосвязей между элементами реальных систем. Обзор и современное развитие такого подхода можно найти в работе [1]. Второй - логический подход основан на анализе и прикладной интерпретации логических взаимосвязей между элементами категорно-топосных систем математики. Типичный представитель такого подхода - работа [2].

Все это приводит к необходимости разработки нового - холистического (англ. whole - целый) подхода к теории систем.

Рассмотрим произвольный объект x=б Set(x), Org(x)с состоящий из N-численного множества Set(x)=А={ а₁…а_N} некоторых элементов а_iО А и имеющий собственную организацию Org(x).

Определение 1. Подмножество A_iН А элементов объекта x назовем его частью.

Объект x имеет 2^N-численное множество A={ A₁…A₂^N} своих частей.

Определение 2. Кортеж m_i=б A_i, r(A_i)с , состоящий из множества A_{i Н} A частей объекта x и множества (k,i)-местных отношений r(A_i) между ними в сигнатуре R_i^(k,i), назовем моделью этого объекта.

Модель m_i=б А, r(А)с является базовой моделью объекта x.

Модели m_i объекта x следует отличать от организации объекта x - абстрактной категории, независящей от частей A_i и отношений r(A_i) между ними.

Определение 3. Множество Org(x) моделей m_iО Org(x) объекта x, связанных между собой изоморфизмами, назовем организацией этого объекта, а сами модели m_i - элементарными представлениями (элементами) этой организации.

Требование наличия изоморфизмов между моделями накладывает два ограничения на модели m_i:

1) равночисленность множеств A_i;

2) общность сигнатур R_i^(k,i) = R^(k).

Определение 4. Кортеж M(Org(x))=б A, r(A)с , состоящий из 2^N-численного множества A частей объекта x и k-местных отношений r(A) между ними в сигнатуре R^(k), связанный с компонентами моделей m_i множества Org(x) соотношениями A_iМ A и r(A_i)М r(A), назовем моделью организации этого объекта.

Модели m_i являются подмоделями модели M(Org(x)) и получаются из нее "стиранием" некоторых элементов A_i и связей r(A_i) между ними.

Любое k-местное отношение r(A_i) может быть редуцировано к одноместным (унарным) и двухместным (бинарным) отношениям [3]. Унарные отношения r(A_i)=A являются частями объекта (его свойствами [4]).

Определение 5. Подмножество Org_intН Org(x), представленное моделями объекта x с унарными отношениями, назовем внутренней организацией этого объекта.

Моделью М_int внутренней организации Org_int объекта x является множество его частей: М_int =A.

Бинарное отношение r(A)Н A² (подмножество декартового квадрата множества A) отражает свойства (взаимодействие, причинно-следственные взаимосвязи) отдельных частей объекта x.

Определение 6. Подмножество Org_extН Org(x), представленное моделями объекта x с бинарными отношениями, назовем внешней организацией этого объекта.

Моделью М_ext внешней организации Org_ext объекта x является кортеж: М_ext=б A, r(A)с в сигнатуре R⁽²⁾.

3. Целостная организация объекта

Определение 7. Организацию Org(x) объекта x, удовлетворяющую условиям:

1) r(A) =A;

2) A№ А,

назовем целостной организацией Who(x) этого объекта.

Первое условие равносильно требованию совпадения моделей М_int=М_ext внутренней и внешней организации (свойств частей объекта и свойств самого объекта). Оно возможно только при числе элементов объекта NЈ 3 и означает отсутствие взаимодействия между частями объекта, их непричинно-следственные взаимосвязи.

Второе условие целостности организации равносильно требованию мновариантной неразличимости элементов объекта x, возможности выделения в нем нетривиальных частей. Неразличимость является превосходной степенью сходства [5]. Она отличается от одинаковости (эквивалентности) элементов их нечеткой индивидуальностью и моделируется рефлексивными симметричными отношениями, которые называются толерантными [6]. Красивыми иллюстрациями толерантных отношений в моделях трех- и N-элементных объектов являются изображенные на рис.1 композиции голландского художника М.К.Эшера [7].

Мновариантная неразличимость элементов объекта может быть реализована при числе элементов NЈ 3.

Единственное число элементов объекта x, удовлетворяющее двум противоречивым условиям целостности его организации - N=3.

Построим модель M(Who(x)) целостной организации Who(x) объекта x, состоящего из множества А={а₁, а₂. а₃} трех элементов.

Такой объект имеет 8-численное множество A своих частей А_i. Распространяя принцип трехэлементности (триадности) состава на носитель каждой модели m_i объекта x, в соответствии с первым ограничением изоморфизмов (раздел 2), представим эти части в виде: АЖ ={ Ж ,Ж ,Ж } , А₁={ а₁,Ж ,Ж } , А₂={ Ж ,а₂,Ж } , А₃={ Ж ,Ж ,а_3} , А₄={ а₁,а₂,Ж } , А₅={ Ж ,а₂,а_3} , А₆={ а₁,Ж ,а_3} , А₇=А.

Общее число N_m моделей m_i объекта x определяется по формуле:

N_m = С₈³ + С₈¹ = 8!/5!/3! + 8!/7! = 56 + 8 = 64,

где С₈³ и С₈¹ - количества сочетаний из 8 подмножеств A, соответственно, по 3 и 1 подмножеству.

В соответствии со вторым условием целостности (раздел 3), отношение r(A_i) в каждой триадной модели m_i является толерантным в сигнатуре R_T⁽²⁾. Характерные для толерантных отношений симметричные стрелки и петли видны на графе базовой триадной толерантной (ТТ) модели m_i=б А, r(A)с , изображенном на рис.2-а.

Построим остальные ТТ-модели объекта x и убедимся в существовании между ними морфизмов. Для начала построим симплекс множества А (рис.2-б), заменив симметричные стрелки отношения R_T⁽²⁾ неориентированными отрезками, а петли - связями с множеством А. Ребра симплекса (части A_i объекта x) имеют общие элементы множества А и, поэтому, также как сами элементы, связаны толерантным отношением r(A) в сигнатуре R_T⁽²⁾. Граф отношения r(A) на множестве A изображен сплошными линиями на рис.2-в. Он состоит из 64 фигур: 35 треугольников, 21 отрезков и 8 точек (вершин) - образующих искомые ТТ-модели m_i. Существование морфизмов между этими моделями следует из одноименности отношений на множествах А и A.

Модель М(Who(x)) целостной организации Who(x) триадного объекта x в форме графа изображена на рис.2-г (симметричные стрелки и петли для простоты опущены). В такой модели неразличимы не только элементы триадного объекта, но и отношения между его частями. Это доказывает, что целостность - принципиально новое (комплексное) свойство организации триадного объекта, отличающееся от свойств его частных моделей.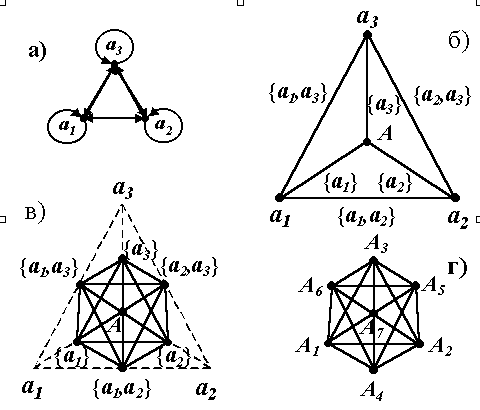

5. Система объекта

Рассмотрим задачу, когда каждый из элементов а_i триадного объекта является, в свою очередь, также триадным объектом а_i=б Set(а_i), Who(а_i)с , который состоит из множества Set(а_i)={ а_i1, а_i1, а_i3} своих элементов а_ij и имеет собственную целостную организацию Who(а_i), модель М(Who(а_i)) которой включает 64 ТТ-модели m_i(а_i) элемента а_i.

Определим какую организацию Org(X) в этом случае имеет сложный триадный объект X=б Set(X), Org(X)с .

Как самостоятельный объект Org(X)=б Set(Org(X)), Org(Org(X))с , такая организация состоит из множества Set(Org(X))={ Who(а₁), Who(а₂), Who(а₃)} своих элементов - целостных организаций Who(а_i) элементов а_i объекта X, и имеет собственную организацию Org(Org(X)).

Модель организации Org(Org(X)) объекта Org(X), с помощью обозначений x=Org(X), а_i=Who(а_i) и А={ а₁, а₂, а_3} , сводится к модели организации Org(x) объекта x, рассмотренной в разделе 2 настоящей работы. Триадность множества А элементов а_i объекта x доказывает целостность организации Org(x)=Who(x). Ее модель М(Who(x)) совпадает с моделью М(Who(x)) (рис. 2-с) при замене подмножеств А на А.

Сложнее выглядит модель М(Org(X)) организации самого объекта X, изображенная в форме графа на рис.3.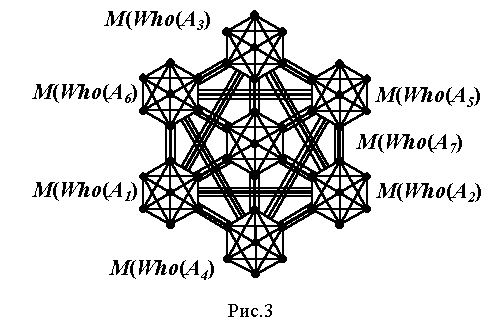

Она представляет собой семь одинаковых по форме семиугольников, все вершины которых связанны между собой толерантными отношениями в сигнатуре R_T⁽²⁾, условно обозначенных на рисунке тройными линиями. Семиугольники расположенны в семи непустых вершинах А_i модели М(Who(x)) и представляют собой графы моделей М(Who(А_i)) целостных организаций семи соответствующих непустых частей А_i объекта Х. Целостность организаций Who(А_i) следует из триадности частей А_i (раздел 4).

Граф каждой модели М(Who(А_i)) состоит из 64 фигур - ТТ-моделей m_i(А_i) части А_i объекта Х. Для одноэлементных частей А₁, А₂ и А₃, состоящих из триадных объектов, соответственно, а₁, а₂ и а₃, формулы расчета числа ТТ-моделей приведены в разделе 4. Для остальных частей А₄ - А₇, состоящих из двух и трех триадных объектов, число ТТ-моделей расчитывается по формуле числа выборок (размещений) с повторением объема N (число элементов) из N+1 (число элементов плюс пропуск): N_m = (N + 1)^N=(3 + 1)³=64.

Модели М(Who(А_i)) целостных организаций частей А_i объекта Х, будем отличать от системы целостных организаций объекта Х - абстрактной категории, независящей от организаций Who(А_i) и отношений между ними.

Определение 8. Множество S(x) моделей М(Who(А_i))О S(x) целостных организаций частей А_i объекта Х, связанных между собой изоморфизмами, назовем системой целостных организаций этого объекта (системой объекта), а сами модели М(Who(А_i)) - представлениями системы.

1. Волкова В.Н., Денисов А.А. Основы теории систем и системного анализа. СПб.: Издательство СПбГТУ, 1999. - 512 с.