 |
||
АДАПТИВНЫЕ МЕТОДЫ ПОДАВЛЕНИЯ МЕШАЮЩИХ СИГНАЛОВ НА ОСНОВЕ
WAVELET-ПРЕОБРАЗОВАНИЯ ПРИМЕНИТЕЛЬНО К ЗАДАЧАМ ГЕОЛОКАЦИИВ.В. Геппенер, М.А. Соколов
Санкт-Петербургский государственный электротехнический университет
“ЛЭТИ” им. В.И.Ульянова (Ленина)Abstract – The task of processing ultrawideband ground probing radar (UWB GPR) signals with the aim of clutter suppression is rather actual for many relevant applications such as, for example, road covering control. Conventional processing techniques use the Fourier transform, which assumes that the signal is stationary. In this paper, the application of a filtering based on wavelet transform to ground roll and high frequency noise suppression is considered.
В настоящее время задача обработки сигналов геолокатора с целью подавления мешающих компонентов является достаточно актуальной при проведении исследования состояния дорожных покрытий, строительных работах и т.п. Обычно для решения этой задачи используется преобразование Фурье, применение которого подразумевает стационарность исследуемого сигнала, в то время как сигналы сверхширокополосного геолокатора являются существенно нестационарными. В данной статье рассматривается применение
wavelet-преобразования для решения указанной задачи, т.к. оно не предполагает стационарности исследуемого сигнала.Основными мешающими компонентами сигнала геолокатора являются высокочастотный шум, обусловленный работой реального прибора и низкочастотный сигнал отражения от поверхности, обладающий высокой амплитудой, который может маскировать сигналы от подповерхностных объектов залегающих на небольших глубинах. Использование частотной фильтрации для подавления сигнала от поверхности приводит к существенному искажению сигнала во временной области, в то время как требуется по возможности сохранить частотное наполнение полезного сигнала, приходящего от объекта. Точно также нежелательно использование преобра-зования Фурье для удаления высоко-частотного шума.
Новым подходом для решения вышеупомянутых задач является использование техники
wavelet-преобразования. Анализ сигналов геолокатора посредством этой техники приводит к представлению исходного одномерного сигнала в виде шкало-временных коэффициетов, причем параметр масштаба (шкалы) может быть интерпретирован как частотный диапазон подлежащий анализу и фильтрации.На рис.1 приведен пример регистрации сигнала, отраженного от небольшого металлического предмета, где горизонтальная ось соответствует времени приема сигнала, т.е. отражает глубину, а вертикальная ось соответствует пространственному перемещению геолокатора.
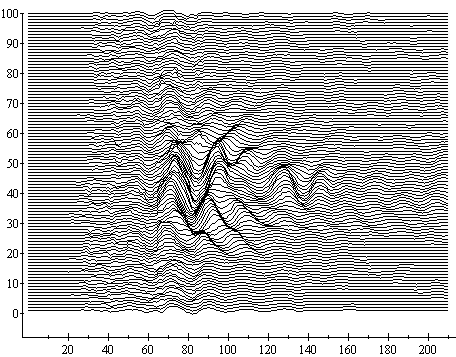
Рис. 1. Типичный сигнал геолокатора
Wavelet-преобразование
Непрерывное wavelet-преобразование определяется как:
![]()
это выражение представляет собой
свертку сигнала ![]()
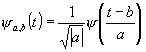
где ![]() и
и ![]()
![]()
где 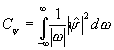
![]()
Подробности могут быть найдены в
[1].Классической реализацией дискретного
wavelet-преобразования DWT является алгоритм Маллат [2]. Однако эта реализация обладает неинвариантностью относительно сдвига. И как показано в [3] дискретное wavelet-преобразование может сильно отличаться у сигналов сдвинутых всего на один отсчет. Чтобы обойти этот эффект было предложено использовать wavelet-преобразование инвариантное к сдвигу (TIDWT) [4]. Данное преобразование не предполагает прореживание на каждом уровне масштаба. Показано [4], что вычисление TIDWT может быть осуществлено с помощью алгоритма сложностиОбозначив максимальный уровень
разложения как ![]()
![]()
где ![]() - матрица
- матрица
![]()
Фильтрация высокочастотного шума
Рассмотрим стандартную модель сигнала с аддитивным гауссовским шумом
:![]() ,
,
где ![]() -
-
![]()
В случае ортогонального
преобразования ![]() компоненты вектора
компоненты вектора ![]()
![]()
где ![]() .
.
Следовательно, получаемая оценка строится следующим образом
:![]()
Однако, так как матрица ![]() , соответствующая
, соответствующая
![]()
где ![]()
Подавление сигнала отражения от поверхности земли
Подавление сигнала отражения от поверхности осуществляется за счет обнуления соответствующих коэффициентов
wavelet-разложения. Причем, коэффициенты подлежащие обнулению выбираются адаптивно на основании анализа расположения нулей функции wavelet-разложения на данном уровне масштаба.На рис.2 приведен пример подавления мешающих компонентов для 45-й реализации сигнала, взятой из кадра реализаций, изображенных на рис.1. На рис.3 изображен кадр реализаций после подавления мешающих компонент. Во всех экспериментах использовалась
wavelet-функция Добеши с параметром 4.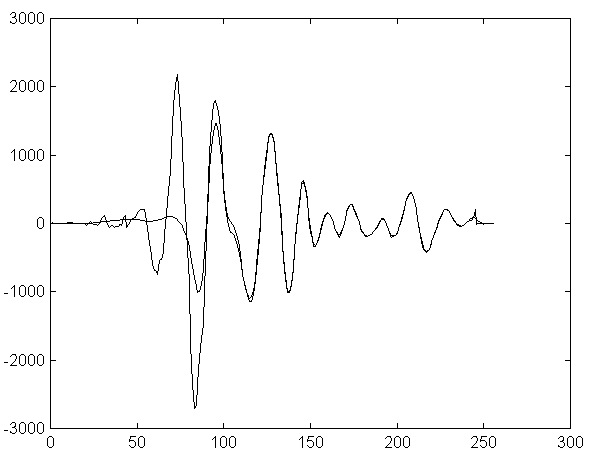
Рис. 2. Пример подавления мешающих сигналов.
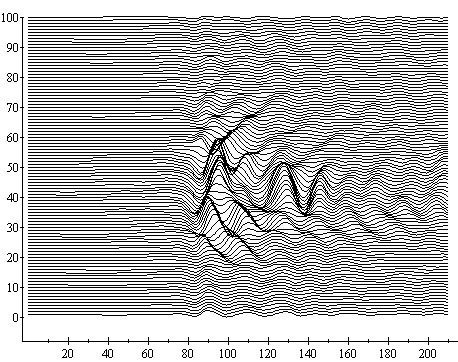
Рис. 3. Кадр сигналов, показанных на Рисунке 1 после подавления мешающих компонентов
Литература
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|