 |
||
ПРИМЕНЕНИЕ
WAVELET-ПРЕОБРАЗОВАНИЯ ДЛЯ КЛАССИФИКАЦИИ АРТЕФАКТОВ В ЭЛЕКТРОЭНЦЕФАЛОГРАФИЧЕСКИХ СИГНАЛАХВ.В. Геппенер, М.Я. Лейтане, Д.А. Черниченко
Санкт-Петербургский государственный электротехнический университет
“ЛЭТИ” им. В.И.Ульянова (Ленина)Abstract – In with paper are described new method of feature description on the basis using wavelet transform. This method are gyved good result in case non-stationary signals. Task of recognition artifacts in EEG signals are discussed. Wavelet transformation and algorithm wavelet packet are described. In the report results of research of developed algorithms on the real records EEG are displayed.
В современных медицинских исследованиях по-прежнему сохраняется большой интерес к методам анализа состояния головного мозга. Основным методом исследования и диагностики состояния работы центральной нервной системы является электроэнцефалография (ЭЭГ). Однако, энцефалограф, как физический прибор, регистрирует не только сигнал, исходящий от коры головного мозга, но и электрические сигналы внемозгового происхождения. Такие сигналы, а также искажения основного сигнала называются артефактами.
Если рассматривать сигнал ЭЭГ как многоканальный случайный процесс, то появление артефакта вызывает резкое изменение статистических свойств случайного процесса. Таким образом, задачу выделения артефактов можно свести к задаче обнаружения резких изменений статистических свойств сигнала. Но поскольку проявление артефактов в сигнале ЭЭГ очень похоже на некоторые феномены, не являющиеся артефактами, а вызванные функциональными нарушениями мозга, возникает задача классификации выделенных
“подозрительных” участков ЭЭГ.Задача классификации состоит из задачи признакового описания объекта и непосредственно алгоритма принимающего решение. В данной статье основное внимание уделено именно адекватному признаковому описанию сигналов артефактов.
Задача признакового описания решалась уже достаточно давно, ранее в литературе встречались следующие подходы
: в качестве признаков предлагалось использовать энергию сигнала в некоторых полосах частот, использование различных статистических характеристик сигнала. Однако, практически всегда результаты последующей классификации были неудовлетворительны и они не были устойчивы. Это связано с тем, что даже непосредственно сигнал ЭЭГ не является стационарным процессом, а при наличии артефакта в сигнале тем более не выполняются условия стационарности. Второй причиной является то, что продолжительность сигнала артефакта по сравнению с частотой дискретизации при записи, невелика (около 0.1-0.3 сек.), а также не представляется возможным точно определить время появления артефакта (существует определенное запаздывание в обнаружении).Авторами предлагается для выделения признаков использовать недавно появившейся математический аппарат, способный, в отличие от преобразования Фурье, описывать нестационарные процессы.
Wavelet-преобразование позволяет раскладывать анализируемую функцию по компактным, хорошо локализованным по времени и частоте, базисам, и при этом имеет полиномиальную сложность. В отличие от кратковременного преобразования Фурье, wavelet-преобразование имеет переменное разрешение по времени и частоте. Оно имеет хорошее разрешение по времени и плохое разрешение по частоте в области высоких частот и хорошее разрешение по частоте и плохое разрешение по времени в области низких частот. Этот подход дает хорошие результаты, особенно когда компоненты сигнала с высокой частотой имеют небольшую длительность, а низкочастотные компоненты - достаточно большую. Сигнал электроэнцефалограммы, как и большинство биологических сигналов, имеет именно такую структуру.С точки зрения цифровой фильтрации,
wavelet-преобразование можно представить с помощью двух, особым образом сконструированных КИХ фильтров и прореживанием по времени: сигнал с пропускается через два фильтра высокой и низкой частоты H(z) и G(z) с частотой среза равной p . Так как в результате фильтрации частотный диапазон уменьшился в два раза, то соответственно в два раза можно уменьшить частоту дискретизации высокочастотной и низкочастотной составляющей. Затем высокочастотная составляющая, называемая wavelet-коэффициентами, запоминается, а с низкочастотной составляющей происходит аналогичная операция, т. е. на каждом этапе происходит фильтрация низкочастотной составляющей, полученной на предыдущем этапе разложения.Такая схема получила название схемы субполосного кодирования (рис. 1).
Сложность вычисления
wavelet-преобразования с помощью схемы субполосного кодирования линейна.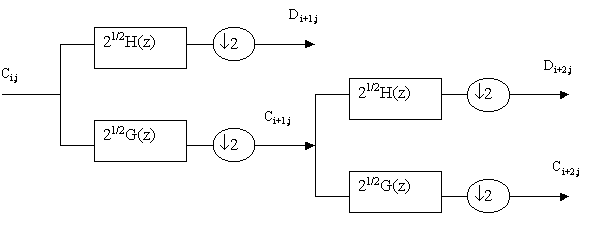
Рис.1. Схема субполосного кодирования.
![]()
![]()
Так как КИХ-фильтры не являются идеальными, то в каждой составляющей произойдет эффект наложения частот, но фильтры построены таким образом, чтобы при последующем восстановлении этот эффект был скомпенсирован, и не происходило потери информации.
При обратном преобразовании (рис. 2) низкочастотная составляющая с
j+2j и высокочастотная составляющая di+2j дополняются нулями и пропускаются через КИХ- фильтры H*(z) и G*(z), однозначно определяемые через H(z) и G(z), в результате чего получается низкочастотная составляющая ci+1j и т. д. Процедура заканчивается полным восстановлением исходного сигнала с.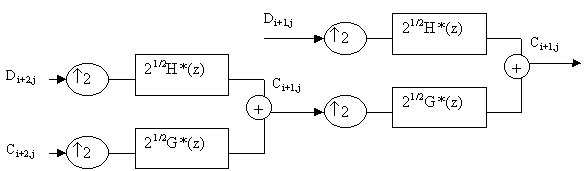
Рис.2. Схема обратного
wavelet-преобразования.![]()
Для выполнения условия точного восстановления, коэффициенты {h
j}и {gj} фильтров H(z) и G(z) соответственно, должны обладать следующими свойствами:![]()
![]()
![]()
Применение wavelet-преобразования позволяет декоррелировать нестационарный сигнал и последующая классификация оказывается более эффективной.
Часто оказывается, что
wavelet-разложение сигнала по классической схеме не всегда оправдано. Это связано с тем, что сигнал раскладывается в сумму сигналов с шириной спектров равной октаве, но для каждого конкретного сигнала такое разбиение не всегда является наилучшим. Мейер и Койфман предложили схему разложения сигнала по пакету wavelet-ов.На каждом уровне последующей фильтрации подвергается не только низкочастотная, но и высокочастотная составляющая. Общая схема фильтрации будет иметь вид двоичного дерева
(рис. 3).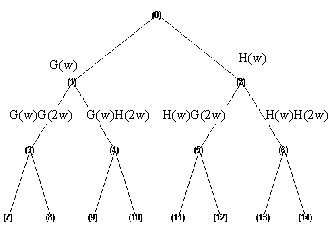
Рис. 3. Граф пакета всплесков.
Пакетом всплесков является любой подграф G полного графа разложения, удовлетворяющий следующим свойствам:
1. Корень дерева принадлежит G.
2. В каждой из вершин граф G либо делится на две части, либо прерывается.
Сигнал, получающийся в каждом узле дерева пакета
wavelet-ов можно интерпретировать как выход с некоторого полосового фильтра. Сложность вычисления по полной схеме составляет О(NlogN).По своей структуре сигнал электроэнцефалограммы состоит из набора ритмов. Принято выделять следующие основные спектральные ритмы
: a ,b ,g ,Q ,d .Распределение ритмов по частотам достаточно хорошо ложиться в схему субполосного кодирования с уменьшением полосы частот на каждом уровне в два раза. При отсутствии патологии ритмы ЭЭГ располагаются по частотам как показано в таблице 1.
Таблица 1. Распределение ритмов ЭЭГ по частотам
Ритм |
Диапазон частот (Гц) |
d -ритм |
0,5 – 3 |
Q -ритм |
4 – 6 |
a -ритм |
8 – 13 |
b -ритм |
13 – 40 |
g -ритм |
> 40 |
Так как каждый узел в
wavelet-пакете отвечает за свою полосу частот, то энергия сигнала в каждом узле, соответствует энергии исходного сигнала в определенной полосе частот. При схеме субполосного кодирования удается хорошо разложить электроэнцефалограммы на составляющие ее ритмы. Потому изменение энергии в какой-либо полосе характеризует изменение того или иного ритма.Для передачи всех ритмов нам достаточно ограничиться wavelet-преобразованием до уровня 5. При разложении сигнала по полному пакету
wavelet-ов в дереве будет 62 узла.Так как дискретное
wavelet-преобразование, в отличие от непрерывного, не инвариантно относительно сдвига по времени, то в качестве признаков берется нормированная плотность энергии wavelet-коэффициентов в узлах дерева пакета wavelet-ов pi,j.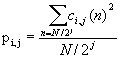 ; где
; где
i = 1 .. K – номер класса,
j = 1 .. 62 – номер признака
сi,j(n) – wavelet-коэффициенты разложения сигнала i-го класса в узле j.
N- длина сигнала.
Если длина классифицируемого сигнала недостаточна, то сигнал переодизируется, для получения достаточной длины- не менее 128 отсчетов.
Так как количество признаков явно избыточно, то для уменьшения числа признаков используется следующая схема: признак включается в модель, если его включает пошаговый дискриминантный анализ и в модели нет прямых потомков этого узла.
Для проведения экспериментов в качестве статистики использовались записи ЭЭГ, полученные в результате плановой клинико-диагностической работы производимой в Институте Эволюционной Физиологии им. И.М. Сеченова Российской Академии Наук. Использовались электроэнцефалограммы восемнадцати пациентов. Все пациенты не имели устойчиво грубых нарушений биоэлектрической активности мозга.
Для анализа использовались пять классов:
Предварительно эксперт просмотрел записи и выделил на них артефакты. Всего на записях экспертом было выделено 208 артефактов.
По результатам работы в модель были включены следующие признаки (рис. 4).
Выбранные узлы отвечают за полосы частот: 0-32 Hz, 48-50 Hz, 50-52 Hz и полностью передают все ритмы электроэнцефалограммы.
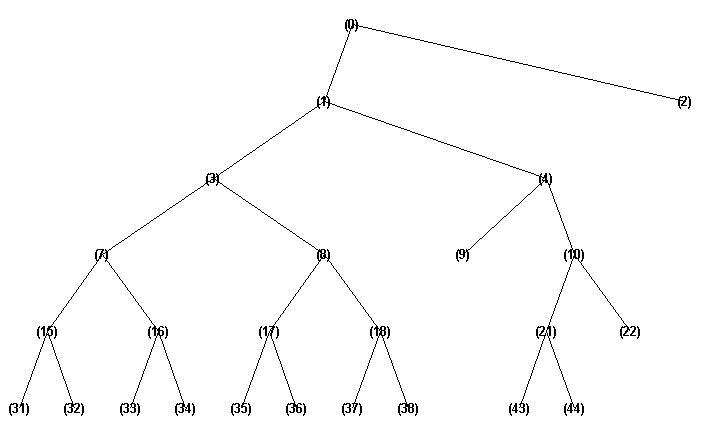
Рис. 4. Узлы, включенные в модель.
В качестве алгоритма, принимающего решения использовался сравнительно простой алгоритм дискриминантного анализа и алгоритм с адаптивным выбором подклассов (АВП), позволяющий строить нелинейные решающие правила.
При классификации с использованием дискриминантного анализа результат правильной классификации равняется 96.15%, при классификации с использованием алгоритма АВП - 96.63%.
Несмотря на то, что алгоритм АВП гораздо мощнее дискриминантного анализа результаты классификации получились практически одинаковыми, что указывает на достаточно простой вид получившейся статистики.
Проведенные исследования показали работоспособность предложенного подхода и адекватности признакового описания. Отметим, однако, что для более обоснованных выводов требуется рассмотреть проблему выбора
wavelet-фильтров.Литература
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|