АППРОКСИМАЦИЯ ПОВЕРХНОСТИ РЕЛЬЕФА

Целью работы является разработка метода представления поверхности рельефа минимальным количеством элементов для повышения производительности систем визуализации сложных пространственных динамических сцен в тренажерных комплексах, когда необходимой оказывается работа в реальном масштабе времени.

Поверхность рельефа может быть задана в виде непрерывной функции высоты y=f(x, z) или в виде множества дискретных элементов аппроксимации. Определить точно функцию высот достаточно трудно, поэтому отдают предпочтение дискретным представлениям. Дискретно заданную поверхность рельефа для обеспечения ее эффективной обработки можно сохранять и обрабатывать как множество уровней разрешения, представляющее собой аппроксимирующие поверхности полного разрешения с определенной погрешностью. Под полным разрешением понимается поверхность рельефа с максимальным уровнем детализации, в которой присутствуют все исходные вершины, описывающие поверхность рельефа.

Ранжирование вершин поверхности рельефа должно обеспечивать определение их рангов по отношению к другим вершинам. Ранг вершины соответствует степени ее влияния на построение аппроксимирующей поверхности. Построение уровней разрешения путем ранжирования вершин сводится к постепенной отбраковке наименее важных вершин.

Чтобы ранжировать вершины поверхности рельефа, необходимо определить критерий сравнения, с помощью которого можно бы было вычислить приоритет любой вершины по отношению к другим оставшимся вершинам.

Особенность предлагаемого метода состоит в том, что используется собственный критерий оценки ранга вершин с помощью линейной регрессии и алгоритм динамического удаления вершин из триангуляции Делоне (ТД) [8].

C помощью линейной регрессии предлагается определить аппроксимирующую плоскость, соответствующую каждой вершине, путем минимизации суммы квадратов отклонений соседних вершин. Приближенно, аппроксимирующую плоскость можно определить через усреднение векторов нормалей всех прилегающих к вершине треугольников. В качестве критерия сравнения вершин предлагается использовать квадрат расстояния от вершины до соответствующей аппроксимирующей плоскости.

Значение критерия каждой вершины позволяет оценить погрешность аппроксимации в случае ее удаления. На рис.1 представлена блок-схема алгоритма ранжирования вершин, где - сортированный список вершин по критерию, которым еще не присвоен ранг.

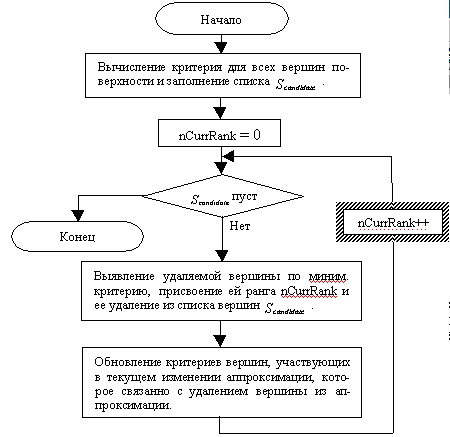
Рис.1. Блок-схема метода ранжирования вершин.

В качестве исходных данных для испытания и качественной и количественной оценки предложенного метода ранжирования взяты два типовых рельефа (гладкий - относительно менее сложная модель и волнистый - относительно более сложная модель).

Можно оценить визуально результат аппроксимации представленный на рис.2. Однако, чтобы получить более точное представление качества аппроксимаций, необходимо оценить погрешность аппроксимации. Для этого определяется погрешность аппроксимации по среднеквадратическому отклонению (СКО). Результаты аппроксимации разных рельефов необходимо нормировать.

В таблице 1.1 и на рис.3 представлена зависимость нормированного среднеквадратического отклонения по диапазону высот от нормированного количества вершин по количеству вершин аппроксимируемой поверхности. Критерий граничных вершин определяется расстоянием до прямой, проходящей через соседние вершины по контуру границы. Контур границы представляет собой ломаную линию, которая охватывает все оставшиеся вершины поверхности рельефа.

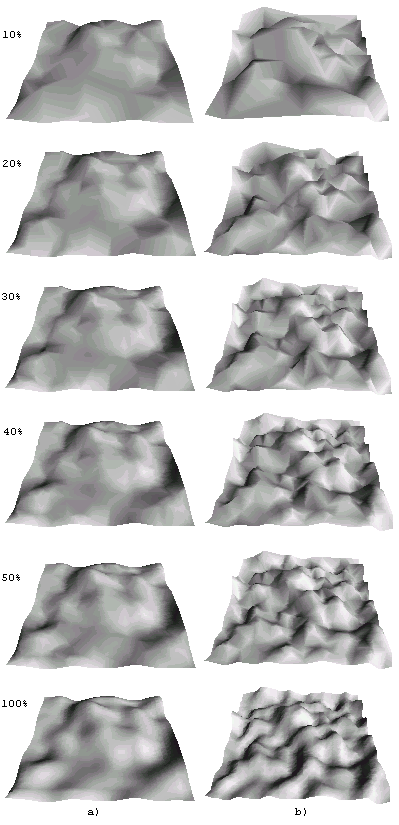
Рис.2 Результаты аппроксимации методом рекурсивного удаления вершин из триангуляции.

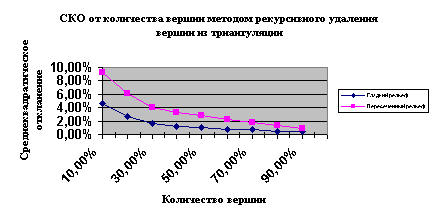
Рис.3 СКО от количества вершин

Предложенный рекурсивный триангуляционный метод ранжирования практически решает проблему аппроксимации поверхности рельефа с минимальным количеством вершин с учетом заданной погрешности. Самостоятельное значение имеют предложения по аппроксимации границ рельефа.

Считаем, что данный подход и соответствуюшие методы ранжирования сущесвенны, когда производительность систем играет решающее значение.

Экспериментальное исследование и визуальное представление аппроксимированных рельефов дает возможность получения конкретных оценок, которые не противоречат полученным в работе результатам.