АДАПТИВНАЯ ДИНАМИЧЕСКАЯ ТЕССЕЛЯЦИЯ

Визуализация рельефов является сложной задачей, поскольку требует одновременного решения двух проблем: высокой производительности и высокого разрешения. Для решения этих проблем предлагается метод визуализации поверхности рельефа местности, в котором повышение производительности системы визуализации осуществляется за счет существенного сокращения количества аппроксимирующих элементов, благодаря фрактальному представлению поверхности рельефа множеством связанных уровней разрешения.

Чтобы уменьшить количество аппроксимирующих элементов в зависимости от удаленности точки наблюдения, поверхность рельефа аппроксимируется с переменной погрешностью с использованием множества уровней разрешения и связей между ними. При этом качество изображения рельефа визуально практически не меняется. На рис.1 слева представлено изображение рельефа с постоянным высоким разрешением (12071 треугольников) и справа - с переменным разрешением (3065 треугольников) в зависимости от удаленности точки наблюдения.

На основании сказанного и данного визуального представления рельефа можно сделать вывод о целесообразности разработки нового подхода представления рельефа с непрерывным переменным разрешением, которое может быть получено за счет использования заранее подготовленных аппроксимирующих поверхностей с различным разрешением и связей между ними.

Рис.1. Изображение рельефа с полным (слева) и с переменным разрешением в зависимости от удаленности точки наблюдения (справа).

Основным требованием к такому подходу является обеспечение локальных модификаций уточнения или упрощения аппроксимирующей поверхности с учетом конкретных условий наблюдения (точки наблюдения, направления взгляда и угла обзора).

Адаптивной динамической тесселяцией (АДТ) называется представление в реальном времени, путем декомпозиции, криволинейной поверхности совокупностью граней-полигонов с разной погрешностью аппроксимации в зависимости от удаленности точки наблюдения.

Ниже рассматривается решение задачи адаптивной динамической тесселяции поверхности рельефа с непрерывным переменным разрешением, которое основывается на многократной предварительной аппроксимации поверхности исходного рельефа фрактальным дроблением элементов аппроксимации. При этом работает механизм иерархической связи между этими аппроксимирующими поверхностями.

На рис.2 представлен алгоритм процесса визуализации поверхности рельефа с переменным разрешением, который состоит из двух основных этапов: предварительный этап определения множества уровней разрешения и связей между ними и этап локальной выборки, сшивки и визуализации поверхности рельефа в интерактивном режиме, в зависимости от позиции и направления взгляда наблюдателя.

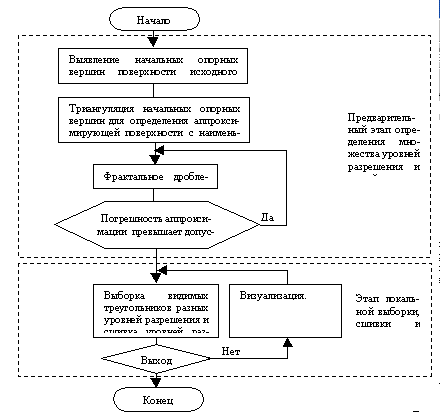
Рис.2.Алгоритм аппроксимации и визуализации поверхности рельефа с множественным разрешением.

2.1 Фрактальная аппроксимация с множественным разрешением

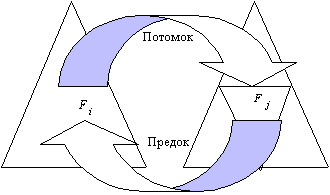
Рис.3 Иерархическая связь “предок-потомок” треугольников.

Для сокращения количества элементов аппроксимации предлагается осуществить адаптивное дробление, как показано на рис.4. Если погрешность определенного элемента аппроксимации не превышает допустимое значение, то нет необходимости его дробить. Однако адаптивное дробление требует отслеживать возможность появления разрывов в аппроксимирующей поверхности и обеспечить сшивку элементов аппроксимации.

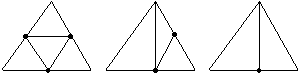
Рис.4 Дробление треугольников.

При адаптивном дроблении макрорельефа на каждой итерации вычисляется центр тяжести каждого треугольника. Далее каждый треугольник разбивается на три внутренние локальные зоны аппроксимации (ЛЗА) отрезками, соединяющими каждую его вершину с его же центром. Если у треугольника есть смежные треугольники, то внутренние ЛЗА, соответствующие общему ребру, объединяются в общую ЛЗА в виде четырехугольника. В каждой из ЛЗА соответствующей каждому ребру определяется погрешность аппроксимации. Если погрешность аппроксимации в пределах зоны превышает допустимое значение, то среди вершин полного разрешения определяется вершина имеющая наибольшее отклонение от ЛЗА, т.е. соответствующая локальному экстремуму по погрешности аппроксимации. Найденный экстремум соединяется с другими экстремумами, соответствующими смежным зонам (если они есть), либо с противоположными вершинами треугольника (если их нет), образуя новые треугольники, как показано на рис.5:

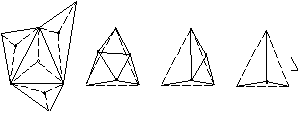
Рис.5 Определение локальных зон аппроксимации.

Процесс аппроксимации завершается, когда достигается допустимая погрешность аппроксимации.

2.2 Адаптивная динамическая тесселяция

Все уровни разрешения объединяются в модель рельефа, со связанными уровнями разрешения , которая содержит не дублированную информацию обо всех уровнях разрешения (некоторые треугольные элементы аппроксимации могут использоваться в нескольких уровнях разрешения) и связей между ними:

Треугольники, входящие в состав модели рельефа, находятся в состоянии “видимый” или “невидимый”. После предварительного этапа формирования модели рельефа с множественным разрешением все треугольники находятся в состоянии “невидимый”. Выборка видимых треугольников, осуществляется адаптивно с помощью волнового метода [6]. С помощью иерархической связи уровней разрешения обеспечивается локальная выборка аппроксимирующих треугольников с разным разрешением в зависимости от удаленности точки наблюдения и динамическая сшивка возможных разрывов на границе зон с разным разрешением как показано на рис.6. Поверхность рельефа, которая находится вблизи точки наблюдения, визуализируется с наименьшей погрешностью, а по мере отдаления - с большей погрешностью, что существенно сокращает количество элементов аппроксимации в процессе визуализации.

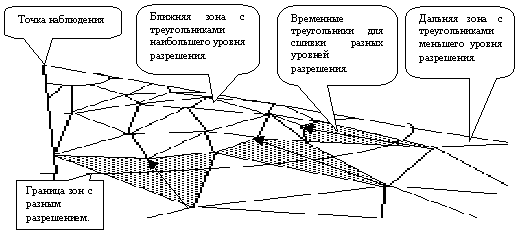
Рис.6. Разделение проекции пирамиды видимости по зонам разрешения и сшивка разных уровней разрешения.

Предложенный адаптивный фрактальный метод динамической тесселяции поверхности рельефа позволяет представить поверхность рельефа минимальным количеством аппроксимирующих треугольников с разной погрешностью аппроксимации.

В ходе экспериментов было обнаружено, что при рекурсивном дроблении фрактального ядра, по мере увеличения количества дроблений, погрешность аппроксимации уровней разрешения монотонно убывает.

.