 |
||
Имитационная модель состояния рефлекторной дуги человека
.И.Б.Чигирева, О.Л.Козлова
Санкт-Петербургский государственный электротехнический университет “ЛЭТИ” им.В.И.Ульянова (Ленина)
Abstract – Diagnostics of a state of the nervimuscular system will be carried out with application of methods of an electromyography. In reply to test impulse some mechanisms of response. Are researched the M - answer and F-answer of the system. The known model of the M - answer does not allow to replicate F-answer. The simulation model for M and F- of the answers grounded on the biophysical theory of creation of the answers as a rest potential and action potential.
Рефлекторная дуга является важной составной частью нервно-мышечной системы человека и множество нарушений системы отражается на состоянии рефлекторной дуги. В связи с этим оценка состояния рефлекторных дуг очень важна для диагностики состояния нервно-мышечной системы в целом.
При диагностике состояния нервно-мышечной системы большой вес имеют стимуляционные методы, заключающиеся в оценке реакции нервно-мышечной системы на тестовое супрамаксимальное импульсное электрическое раздражение. [1]
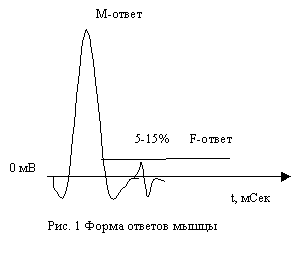
В ответ на тестовый импульс включаются несколько механизмов реакции, отражающихся в соответствующих ответах. Настоящая работа посвящена исследованию М-ответа и F-ответа системы (рис. 1). Их расшифровка имеет большое значение для понимания механизмов нарушения в подсистеме “мотонейрон-мышца”.
М-ответ – вызванный потенциал мышцы, являющийся суммарным синхронным разрядом двигательных единиц мышцы в ответ на супрамаксимальное электрическое раздражение нерва. F-ответ – импульс, возникающий в результате антидромного распространения импульса и следующей за ним возвратной активации, охватывающей лишь группу самых возбудимых на данный момент клеток, составляющих приблизительно 5% от общего числа клеток. [1]
Амплитуда, форма, размах колебаний, длительность, площадь под кривой и время появления ответов имеют большую диагностическую ценность. Однако традиционные методы предполагают поверхностную оценку этих параметров, что позволяет дать лишь общую характеристику состояния подсистемы. Поэтому возникает задача исследовать состояние и проводимость отдельных элементов нервно-мышечной системы по цепочкам: стимул – мотонейрон - мышца и стимул – мотонейрон - спинной мозг – мотонейрон – мышца, в результате прохождения по которым и формируются исследуемые ответы. Цепочки включают в себя множество двигательных нейронов, мышечных волокон и связей между ними, имеющих свои специфические особенности при патологических нарушениях. Таким образом, объектом исследования является сложная система. [2]
Одним из наиболее перспективных методов в исследовании сложных систем является метод математического моделирования. Ранее была разработана модель М-ответа, учитывающая состояние отдельных элементов системы.
В основе нового подхода лежит имитационное моделирование механизмов формирования М-ответа и нарушений в функционировании подсистемы “мотонейрон - мышца”. При формировании ПД на поверхности мышцы используется так называемая теория “телесного угла”, согласно которой моделируется ПД отдельного мышечного волокна. Согласно этой теории, ПД в месте записи определяется зарядами на осевых сечениях волокна, являющихся границами возбужденной зоны мышцы. Величина его пропорциональна величине телесного угла в вершиной в точке записи и основанием в виде осевого сечения. На рис.2 показано формирование потенциала Р поверхностными зарядами отдельного мышечного волокна на границах фронта деполяризации (фронт S1) и фронта реполяризации (фронт S2).
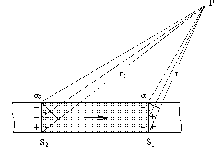
Рис.2. Схема формирования потенциала (Р) в точке съема сигнала;
a 1, a 2 – углы между поперечными сечениями волокна (фронт S1 или S2) и конуса с вершиной в точке съема сигнала; r1, r2 – расстояния между точкой съема сигнала и серединами соответствующих фронтовПотенциал Р в точке записи может быть вычислен следующим образом
![]()
где
a 1, a 2 – углы между поперечными сечениями волокна и направлением на электрод записи; r1, r2 – расстояния от точки съема до середин соответствующих фронтов; к – коэффициент пропорциональности.ПД всей мышцы является суперпозицией потенциалов отдельных волокон. Следовательно, ПД мышцы в точке записи, в некоторый момент времени после стимуляции, может быть записан следующим образом
![]()
где
P(t) – ПД мышцы как функция от времени; N – число мышечных волокон; Pi(t-t i) – ПД отдельного мышечного волокна с задержкой t i. Задержка включает несколько составляющих, среди которых для определения СП по нервному волокну необходимо найти время проведения возбуждения по нервному волокну от момента стимуляции до момента возбуждения мышечного волокна. Чтобы исключить остальные составляющие, необходимо найти разницу задержек возбуждения отдельного мышечного волокна при стимуляции в двух различных точках. Следовательно, СП i –го мотонейрона может быть найдена по формуле 3:![]()
где L
1, L2 – расстояния от точки стимуляции до точки съема сигнала; t 1,t 2 – задержки проведения.В основу алгоритма диагностики положено совмещение модельного и реального М-ответов. Процедура минимизации рассогласования модельного и реального ответов проводится путем целенаправленной настройки параметров модели. К основным параметрам модели относятся распределение
задержек возбуждения мышечных волокон, его среднее и дисперсия, скорость проведения по мышечному волокну, скорость реполяризации, расстояние между записывающим электродом и центром области концевых пластинок, размеры мышцы и ее глубина под кожей, локальных блоков проведения в любой части цепи: мотонейрон – синапс – мышечное волокно.Тем не менее аппарат, заложенный в эту модель, не позволяет воспроизводить вторую компоненту реакции системы – F-ответ. Поэтому разрабатывается имитационная модель для М- и F- ответов, базирующаяся на биофизической теории формирования ответов исходя из характеристик проводимости клеточной мембраны и концентрации ионов, создающих на мембране потенциал покоя (ПП) и потенциал действия (ПД).
В отсутствие раздражения на мембране снимается ПП – постоянная величина в –60мВ, а при раздражении – ПД (около 40 мВ). [3]
При определенных условиях внешнего раздражения мембраны – большой амплитуде и малой длительности (условия супрамаксимального раздражения) на мембране регистрируется ПД сложной формы.
Поскольку клеточная мембрана на участках, соседних с возбужденным, также имеет свойство возбудимости, ПД распространяется на соседние участки, практически не теряя ни амплитуды (за которую ответственна концентрация ионов и проводимость мембраны), ни формы. Таким образом ПД с определенной скоростью распространяется по нервному волокну.
Все эти явления описаны еще в конце прошлого века в теории физики нервного импульса Ходжкина и Хаксли. Ими же предложена полуэмпирическая модель, описывающая изменение потенциала на мембране с помощъю шести дифференциальных уравнений, действующих в определенные промежутки времени и имеющая хорошую сходимость с опытом. [3]
Благодаря использованию этой модели для имитационного моделирования ответов рефлекторной дуги на тестовое супрамаксимальное электрическое раздражение возможно хотя бы частично ответить на вопрос о происхождении и поведении F-ответа мышцы.[4]
При стимуляции формируется локальный ответ системы, обусловленный потоками ионов солей, открывающих каналы проводимости для ионов натрия. Затем регистрируется потенциал, обусловленный потоком самих ионов натрия через мембрану – натриевым током. Суммарный потенциал со всех нервных волокон, возбуждаемых при супрамаксимальном раздражении вполне сравним по амплитуде с величиной самого раздражения, что, возможно и обуславливает появление F-ответа, как локального ответа мембраны на повторное раздражение, наведенное с соседних участков мембраны. Так как после прохождения натриевого тока на достижение первоначального состояния мембране нужно время порядка 0,5 мСек, повторной генерации натриевого тока не происходит (рис. 3).
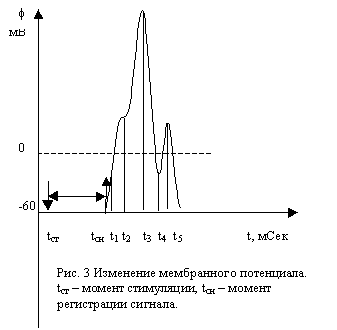
Согласно модели Ходжкина-Хаксли такая кривая будет описываться следующими уравнениями [ 2 ]:
![]() , (1)
, (1)
при t<t
1,![]() , (2)
, (2)
при t
1 Ј t < t2 и t4 Ј t < t5![]() ,
(3)
,
(3)
при t
2 Ј t < t3![]() , (4)
, (4)
при t
4 > t і t3 ,![]() (5) при t5 Ј t
(5) при t5 Ј t
где:
![]() - стимулирующее воздействие,
- стимулирующее воздействие,
f
- мембранный потенциал,f0
- потенциал покоя мембраны –60мВf1
, f2 - значения f в моменты времени t0, t1 и t2, соответственно. При описании третьего пика в уравнениях (2) и (5) вместо f1 и f2 используются значения f4 и f5, определяемые как f(t4) и f(t5),g – проводимость мембраны – характеристика способности мембраны пропускать ионы.
g1, g2, g4 и g5 – проводимости в моменты времени t1, t2, t4 и t5, соответственно,
С – концентрация ионов.
Уравнение (1) описывает пассивное поведение мембраны при возбуждении. Когда наступает момент начала локального ответа t1 в силу вступает уравнение (2). Затем наступает момент включения натриевого тока t2 и в силу вступает уравнение (3). В момент t3 натриевый ток выключается и в силу вступает уравнение (4). Второй локальный ответ включается в момент t4 и в силу снова вступает уравнение (2). Уравнение (3) имеет решение (5), которое вступает в силу в момент t5 выключения локального ответа и описывает поведение системы при уменьшении мембранного потенциала до величины ПП.
На основе этих уравнений строится модель, имитирующая реакцию рефлекторной дуги на тестовое супрамаксимальное электрическое раздражение. При этом подставляются временные параметры, полученные ранее при проведении экспериментов на икроножной и камбаловидной мышцах здоровых людей. Концентрация ионов и проводимость мембраны здорового человека также изветсны. В описываемом случае, первый пик сложной формы будет являться М-ответом системы, а следующий за ним пик повторного локального возбуждения будет F-ответом. Для воспроизведения кривой при патологии эти величины изменяются, что дает возможность более точной постановки диагноза и выбора адекватных методов лечения.
Сейчас проводятся машинные эксперименты с моделью и предварительная оценка точности получаемых данных путем вычисления среднеквадратического отклонения результатов машинного и проведенного ранее медицинского экспериментов.
Литература
1. С.Т.Байкушев и др. Стимуляционная электромиография и электронейрография в клинике нервных болезней. М.: Наука, 1974.
2. Е.В. Чурносов, В.Н. Команцев, О.Л. Филонова. Имитационное моделирование реакции подсистемы “мотонейрон-мышца” на тестовое электрическое раздражение//Известия ГЭТУ: Сборник научных трудов. СПб., 1998.С. 21-25.
3. М.В. Волькенштейн Биофизика 2-е изд. М.: Наука, 1988.
4. Гидиков А.А. Теоретические основы электромиографии Л.: Наука, 1975.
| Site of Information
Technologies Designed by inftech@webservis.ru. |
|